人教版数学七年级下册5.1.2垂线 课件 (共29张PPT)
文档属性
| 名称 | 人教版数学七年级下册5.1.2垂线 课件 (共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
5.1.2 垂线
知识点
相似图形
感悟新知
1
1. 定义:
当两条直线相交所形成的四个角中,有一个角是直角时,就称这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足 .
特别解读
垂直的定义具有双重作用,已知直角得线垂直,已知线垂直得直角.
感悟新知
2. 推理格式:
如图5.1-10,直线AB,CD 相交于点O.
因为∠ AOC=90°(已知),
所以AB ⊥ CD(垂直的定义).
反过来:因为AB ⊥ CD(已知),
所以∠ AOC=90°(垂直的定义).
感悟新知
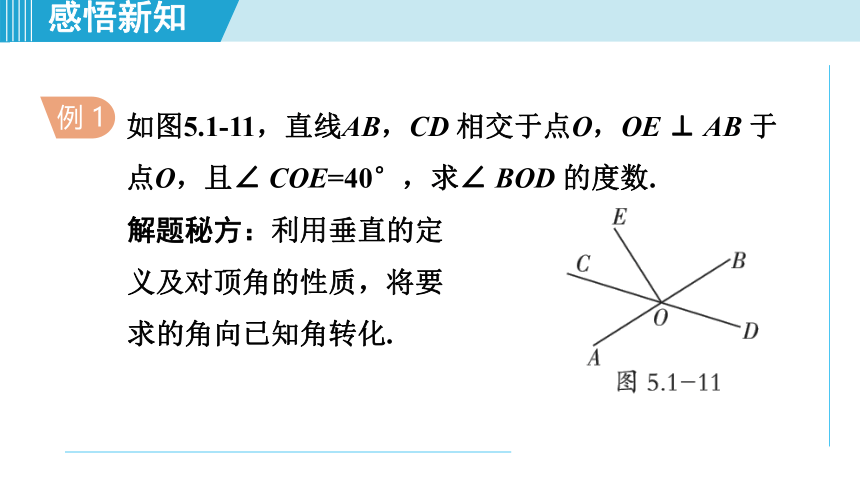
如图5.1-11,直线AB,CD 相交于点O,OE ⊥ AB 于
点O,且∠ COE=40°,求∠ BOD 的度数.
例 1
解题秘方:利用垂直的定义及对顶角的性质,将要求的角向已知角转化.
感悟新知
解:因为OE ⊥ AB,
所以∠ AOE=90°.
又因为∠ AOE= ∠ AOC+ ∠ COE,∠ COE=40°,
所以∠ AOC=90°-40°=50°.
所以∠ BOD= ∠ AOC=50°
感悟新知
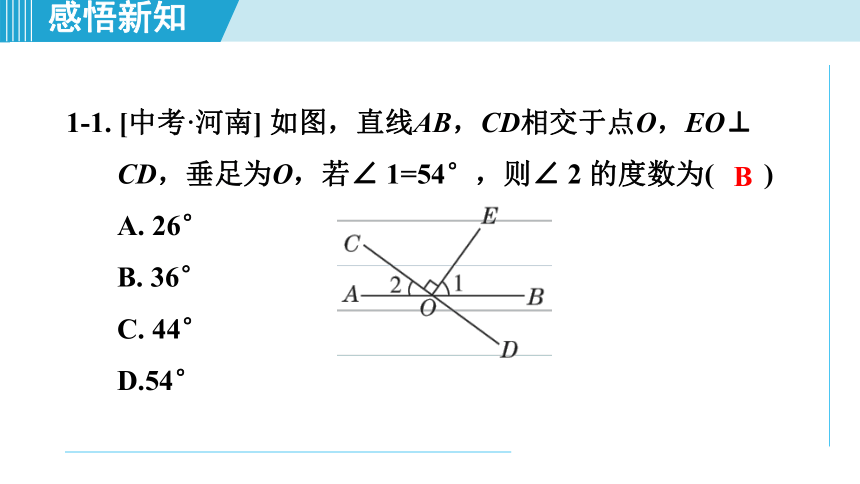
1-1. [中考·河南] 如图,直线AB,CD相交于点O,EO⊥ CD,垂足为O,若∠ 1=54°,则∠ 2 的度数为( )
A. 26°
B. 36°
C. 44°
D.54°
B
感悟新知
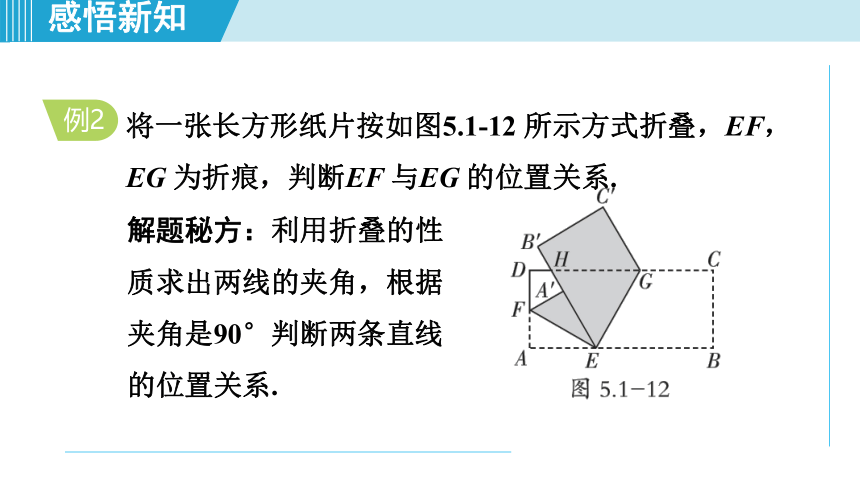
将一张长方形纸片按如图5.1-12 所示方式折叠,EF,
EG 为折痕,判断EF 与EG 的位置关系.
解题秘方:利用折叠的性质求出两线的夹角,根据夹角是90°判断两条直线的位置关系.
例2
感悟新知
解:因为三角形A′EF 是由三角形AEF 折叠得到的,四边形B′EGC′是由四边形BEGC 折叠得到的,
所以∠ AEF= ∠ A′EF,∠ BEG= ∠ B′EG.
所以∠ A′EF= ∠ AEA′,∠ A′EG= ∠ A′EB.
所以∠ FEG= ∠ A′EF+ ∠ A′EG= ∠ AEA′+
∠ A′EB= (∠ AEA′+∠ A′EB)= ×180°=90°.
所以EF ⊥ EG.
邻补角的平分线互相垂直.
感悟新知
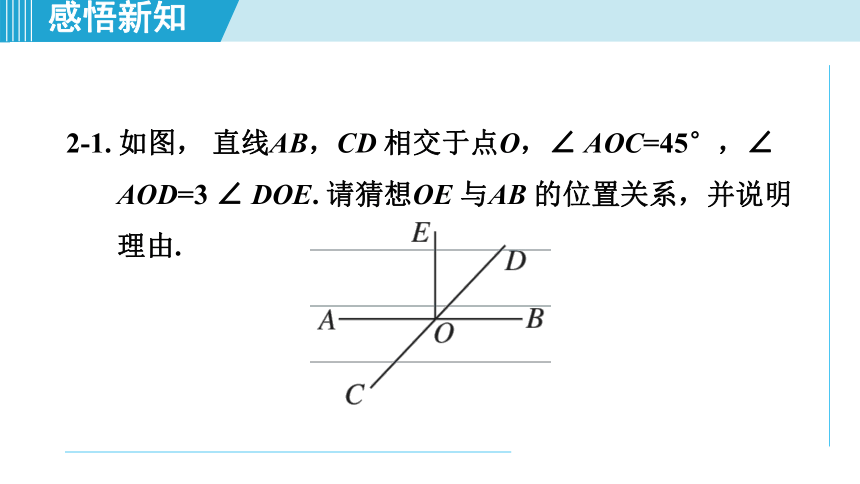
2-1. 如图, 直线AB,CD 相交于点O,∠ AOC=45°,∠ AOD=3 ∠ DOE. 请猜想OE 与AB 的位置关系,并说明理由.
感悟新知
解:OE⊥AB.理由如下:因为∠AOC=45°,
所以∠AOD=180°-∠AOC=180°-45°=135°.
因为∠AOD=3∠DOE,
所以3∠DOE=135°,所以∠DOE=45°,
所以∠AOE=∠AOD-∠DOE=135°-45°=90°,所以OE⊥AB.
知识点
垂线的画法及性质
感悟新知
2
1. 垂线的画法:
经过一点(已知直线上或直线外),画已知直线的垂线,
步骤如下:
感悟新知
步骤 内容 示图
一落 让三角尺的一条直角 边落在已知直线上, 使其与已知直线重合 过点P 作直线l 的垂线:
点P 在直线l 外 点P 在直线l 上
二移 沿已知直线移动三角 尺,使其另一条直角 边经过已知点 三画 沿此直角边画直线, 则这条直线就是已知 直线的垂线 感悟新知
2. 垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.
特别提醒
性质中的唯一性有两个关键条件不能少:一是“同一平面”;二是过一点,这一点可以在直线上也可以在直线外.
感悟新知
在图5.1-13 中,分别过点P 作AB 的垂线.
例 3
感悟新知
解题秘方:利用三角尺根据画垂线的步骤进行操作.
温馨提示:作线段的垂线时,垂足不一定在线段上. 若不在线段上,则必须将线段用虚线延长.
感悟新知
解:如图5.1-14.
感悟新知
3-1. 如图,分别过点P作线段MN 的垂线.
感悟新知
解:如图所示.
知识点
垂线段及点到直线的距离
感悟新知
3
1. 垂线段:
特别解读
垂线、垂直与垂线段之间的区别与联系:
1. 区别:垂线是一条与已知直线垂直的直线;垂直是两条直线之间的位置关系;垂线段是一条与已知直线垂直的线段.
2. 联系:垂线段所在的直线是已知直线的垂线;垂线段所在的直线与已知直线垂直.
感悟新知
(1)定义:过直线外一点画已知直线的垂线,连接这点与垂足之间的线段,叫做这点到已知直线的垂线段.
(2)性质:连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
感悟新知
2. 点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
(1)垂线段与点到直线的距离的区别:垂线段是一个几何图形,而点到直线的距离是一个数量,是垂线段的长度.
感悟新知
(2)点到直线的距离与两点间的距离的区别:
两点间的距离 点到直线的距离
定义 连接两点的线段的长度 直线外一点到这条直线的垂线段的长度
性质 两点之间,线段最短 垂线段最短
感悟新知
(1)如图5.1-15,在三角形ABC 中,∠ ACB=90°,CD ⊥ AB,垂足为D. 若AC=4 cm,BC=3 cm,AB=
5 cm,则点A到直线BC 的距离为______ cm,点B 到直线AC 的距离为______ cm,
点C 到直线AB 的距离为
______ cm.
例4
4
3
2.4
感悟新知
解题秘方:根据点到直线的距离的定义,找出垂线段.
解:根据点到直线的距离的定义可知,
点A 到直线BC 的距离是线段AC 的长,
点B 到直线AC 的距离是线段BC 的长,
点C 到直线AB 的距离是线段CD 的长.
因为三角形ABC 的面积S= AC·BC= AB·CD,
所以AC·BC=AB·CD,进而可得CD=2.4 cm.
面积法求直角三角形斜边上的高
感悟新知
(2)点P 为直线m 外一点,点A,B,C 为直线m 上的三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P 到直线m 的距离( )
A. 等于4 cm B. 等于2 cm
C. 小于2 cm D. 不大于2 cm
D
感悟新知
解题秘方:根据点到直线的距离的定义,找出垂线段.
解:点到直线的距离是该点到这条直线的垂线段的长度,而垂线段是该点与直线上各点的连线中最短的. 从条件看,PC是三条线段中最短的,但不一定是所有连线中最短的,所以点P 到直线m 的距离应该是不大于2 cm.
感悟新知
4-1. 如图,一辆汽车在笔直的公路上由A 向B行驶,M,N 是位于公路AB 两侧的两个学校,若汽车在公路上行驶时会对学校教学造成影响,
试通过画图分别确定出汽车
行驶时对两所学校影响最大
的位置.
感悟新知
解:如图,C点是汽车对M学校影响最大的位置,D点是汽车对N学校影响最大的位置.
课堂小结
垂线
垂线段
垂线
性质
点到直线的距离
垂线的性质
5.1.2 垂线
知识点
相似图形
感悟新知
1
1. 定义:
当两条直线相交所形成的四个角中,有一个角是直角时,就称这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足 .
特别解读
垂直的定义具有双重作用,已知直角得线垂直,已知线垂直得直角.
感悟新知
2. 推理格式:
如图5.1-10,直线AB,CD 相交于点O.
因为∠ AOC=90°(已知),
所以AB ⊥ CD(垂直的定义).
反过来:因为AB ⊥ CD(已知),
所以∠ AOC=90°(垂直的定义).
感悟新知
如图5.1-11,直线AB,CD 相交于点O,OE ⊥ AB 于
点O,且∠ COE=40°,求∠ BOD 的度数.
例 1
解题秘方:利用垂直的定义及对顶角的性质,将要求的角向已知角转化.
感悟新知
解:因为OE ⊥ AB,
所以∠ AOE=90°.
又因为∠ AOE= ∠ AOC+ ∠ COE,∠ COE=40°,
所以∠ AOC=90°-40°=50°.
所以∠ BOD= ∠ AOC=50°
感悟新知
1-1. [中考·河南] 如图,直线AB,CD相交于点O,EO⊥ CD,垂足为O,若∠ 1=54°,则∠ 2 的度数为( )
A. 26°
B. 36°
C. 44°
D.54°
B
感悟新知
将一张长方形纸片按如图5.1-12 所示方式折叠,EF,
EG 为折痕,判断EF 与EG 的位置关系.
解题秘方:利用折叠的性质求出两线的夹角,根据夹角是90°判断两条直线的位置关系.
例2
感悟新知
解:因为三角形A′EF 是由三角形AEF 折叠得到的,四边形B′EGC′是由四边形BEGC 折叠得到的,
所以∠ AEF= ∠ A′EF,∠ BEG= ∠ B′EG.
所以∠ A′EF= ∠ AEA′,∠ A′EG= ∠ A′EB.
所以∠ FEG= ∠ A′EF+ ∠ A′EG= ∠ AEA′+
∠ A′EB= (∠ AEA′+∠ A′EB)= ×180°=90°.
所以EF ⊥ EG.
邻补角的平分线互相垂直.
感悟新知
2-1. 如图, 直线AB,CD 相交于点O,∠ AOC=45°,∠ AOD=3 ∠ DOE. 请猜想OE 与AB 的位置关系,并说明理由.
感悟新知
解:OE⊥AB.理由如下:因为∠AOC=45°,
所以∠AOD=180°-∠AOC=180°-45°=135°.
因为∠AOD=3∠DOE,
所以3∠DOE=135°,所以∠DOE=45°,
所以∠AOE=∠AOD-∠DOE=135°-45°=90°,所以OE⊥AB.
知识点
垂线的画法及性质
感悟新知
2
1. 垂线的画法:
经过一点(已知直线上或直线外),画已知直线的垂线,
步骤如下:
感悟新知
步骤 内容 示图
一落 让三角尺的一条直角 边落在已知直线上, 使其与已知直线重合 过点P 作直线l 的垂线:
点P 在直线l 外 点P 在直线l 上
二移 沿已知直线移动三角 尺,使其另一条直角 边经过已知点 三画 沿此直角边画直线, 则这条直线就是已知 直线的垂线 感悟新知
2. 垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.
特别提醒
性质中的唯一性有两个关键条件不能少:一是“同一平面”;二是过一点,这一点可以在直线上也可以在直线外.
感悟新知
在图5.1-13 中,分别过点P 作AB 的垂线.
例 3
感悟新知
解题秘方:利用三角尺根据画垂线的步骤进行操作.
温馨提示:作线段的垂线时,垂足不一定在线段上. 若不在线段上,则必须将线段用虚线延长.
感悟新知
解:如图5.1-14.
感悟新知
3-1. 如图,分别过点P作线段MN 的垂线.
感悟新知
解:如图所示.
知识点
垂线段及点到直线的距离
感悟新知
3
1. 垂线段:
特别解读
垂线、垂直与垂线段之间的区别与联系:
1. 区别:垂线是一条与已知直线垂直的直线;垂直是两条直线之间的位置关系;垂线段是一条与已知直线垂直的线段.
2. 联系:垂线段所在的直线是已知直线的垂线;垂线段所在的直线与已知直线垂直.
感悟新知
(1)定义:过直线外一点画已知直线的垂线,连接这点与垂足之间的线段,叫做这点到已知直线的垂线段.
(2)性质:连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
感悟新知
2. 点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
(1)垂线段与点到直线的距离的区别:垂线段是一个几何图形,而点到直线的距离是一个数量,是垂线段的长度.
感悟新知
(2)点到直线的距离与两点间的距离的区别:
两点间的距离 点到直线的距离
定义 连接两点的线段的长度 直线外一点到这条直线的垂线段的长度
性质 两点之间,线段最短 垂线段最短
感悟新知
(1)如图5.1-15,在三角形ABC 中,∠ ACB=90°,CD ⊥ AB,垂足为D. 若AC=4 cm,BC=3 cm,AB=
5 cm,则点A到直线BC 的距离为______ cm,点B 到直线AC 的距离为______ cm,
点C 到直线AB 的距离为
______ cm.
例4
4
3
2.4
感悟新知
解题秘方:根据点到直线的距离的定义,找出垂线段.
解:根据点到直线的距离的定义可知,
点A 到直线BC 的距离是线段AC 的长,
点B 到直线AC 的距离是线段BC 的长,
点C 到直线AB 的距离是线段CD 的长.
因为三角形ABC 的面积S= AC·BC= AB·CD,
所以AC·BC=AB·CD,进而可得CD=2.4 cm.
面积法求直角三角形斜边上的高
感悟新知
(2)点P 为直线m 外一点,点A,B,C 为直线m 上的三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P 到直线m 的距离( )
A. 等于4 cm B. 等于2 cm
C. 小于2 cm D. 不大于2 cm
D
感悟新知
解题秘方:根据点到直线的距离的定义,找出垂线段.
解:点到直线的距离是该点到这条直线的垂线段的长度,而垂线段是该点与直线上各点的连线中最短的. 从条件看,PC是三条线段中最短的,但不一定是所有连线中最短的,所以点P 到直线m 的距离应该是不大于2 cm.
感悟新知
4-1. 如图,一辆汽车在笔直的公路上由A 向B行驶,M,N 是位于公路AB 两侧的两个学校,若汽车在公路上行驶时会对学校教学造成影响,
试通过画图分别确定出汽车
行驶时对两所学校影响最大
的位置.
感悟新知
解:如图,C点是汽车对M学校影响最大的位置,D点是汽车对N学校影响最大的位置.
课堂小结
垂线
垂线段
垂线
性质
点到直线的距离
垂线的性质
