人教B版(2019)数学必修第一册 3_1_2函数的单调性 课件(共40张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册 3_1_2函数的单调性 课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 22:07:32 | ||
图片预览









文档简介
(共40张PPT)
函数的单调性 (1)
本节目标
1.通过已学过的函数特别是二次函数,理解函数的单调性及其几何意义.
2.学会运用函数图象理解和研究函数的性质.
3.能够熟练应用定义判断与证明函数在某区间上的单调性.
本节目标
课前预习
(1)增函数、减函数的概念是什么?
(2)如何表示函数的单调区间?
(3)函数的单调性和单调区间有什么关系?
预习课本,思考并完成以下问题
课前小测
1.如果函数f(x)在[a,b]上是增函数,那么对于任意的x1,x2∈[a,b](x1≠x2),下列结论中不正确的是( )
A. >0 B.(x1-x2)[f(x1)-f(x2)]>0
C.f(a)0
C
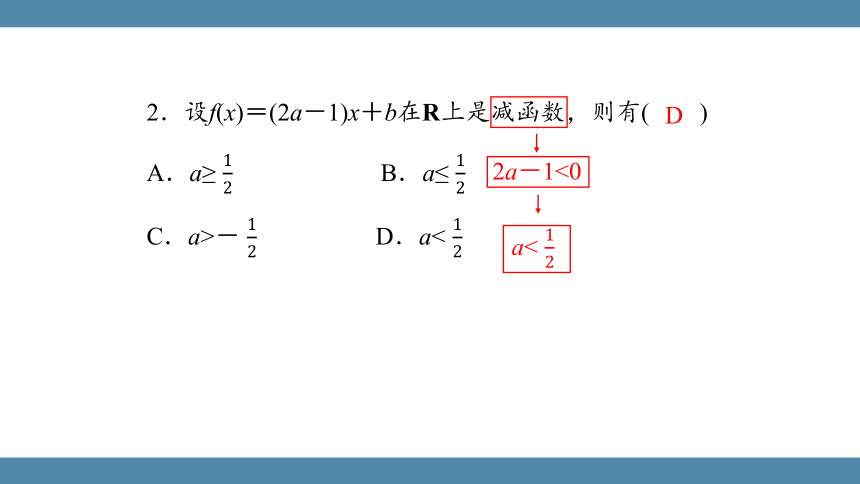
2.设f(x)=(2a-1)x+b在R上是减函数,则有( )
A.a≥ B.a≤
C.a>- D.a<
D
2a-1<0
a<
3.函数f(x)=2x2-mx+3,当x∈[-2,+∞)时,f(x)为增函数,当x∈(-∞,-2]时,函数f(x)为减函数,则m等于( )
A.-4 B.-8
C.8 D.无法确定
B
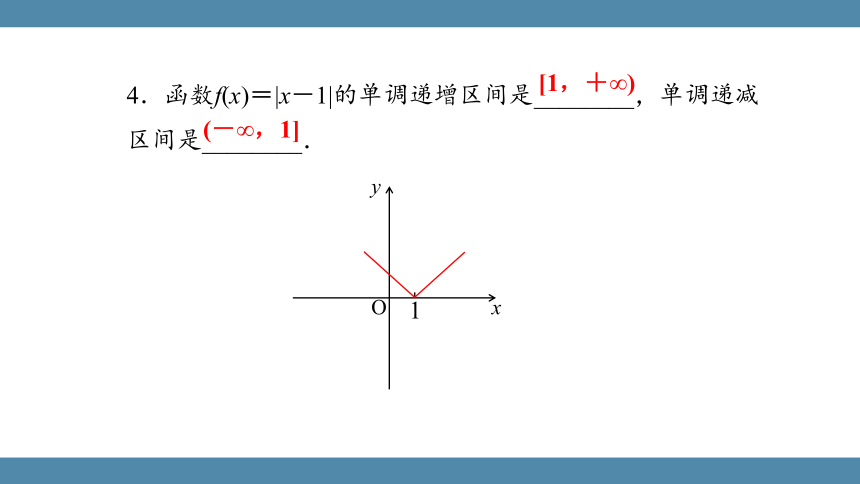
4.函数f(x)=|x-1|的单调递增区间是________,单调递减区间是________.
(-∞,1]
[1,+∞)
O
x
y
1
新知探究
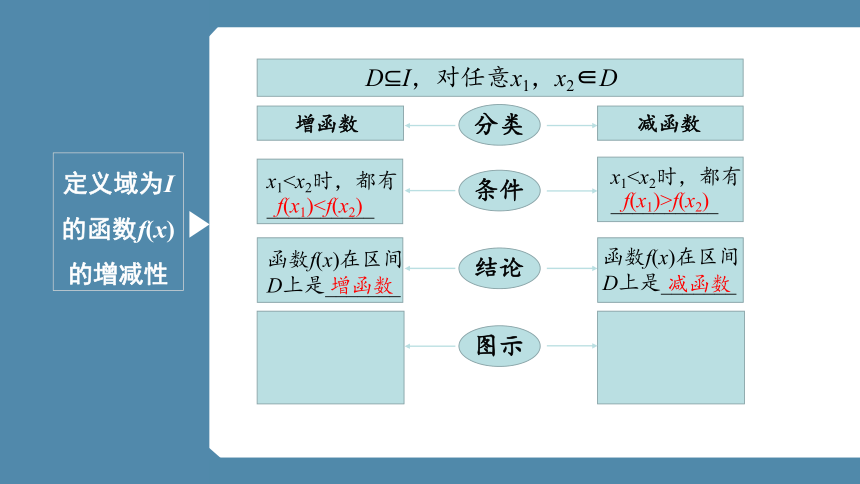
定义域为I的函数f(x)的增减性
DI,对任意x1,x2∈D
分类
条件
结论
图示
减函数
增函数
x1x1函数f(x)在区间D上是_______
函数f(x)在区间D上是_______
f(x1)f(x1)>f(x2)
增函数
减函数
定义中的x1,x2有以下3个特征
(1)任意性,即“任意取x1,x2”中“任意”二字绝不能去掉,证明时不能以特殊代替一般;
(2)有大小,通常规定x1(3)属于同一个单调区间.
知识点睛
单调性与单调区间
如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间上具有(严格的) _________,区间D叫做y=f(x)的___________.
单调性
单调区间
一个函数出现两个或者两个以上的单调区间时,不能用“∪”连接,而应该用“和”连接.
如函数y=在(-∞,0)和(0,+∞)上单调递减,却不能表述为:函数y=在(-∞,0)∪(0,+∞)上单调递减.
易错提醒
题型突破
典例深度剖析 重点多维探究
题型一 求函数的单调区间
[例1] 求下列函数的单调区间,并指出该函数在其单调区间上是增函数还是减函数.
(1)f(x)=-;
(2)f(x)=
(3)f(x)=-x2+2|x|+3.
[例1] 求下列函数的单调区间,并指出该函数在其单调区间上是增函数还是减函数.
(1)f(x)=-;
函数f(x) =-的单调区间为(-∞,0),(0,+∞)
其在(-∞,0),(0,+∞)上都是增函数
[例1] 求下列函数的单调区间,并指出该函数在其单调区间上是增函数还是减函数.
(2)f(x)=
当x≥1时,f(x)是增函数,当x<1时,f(x)是减函数,
所以f(x)的单调区间为(-∞,1),[1,+∞),
并且函数f(x)在(-∞,1)上是减函数,在[1,+∞)上是增函数.
[例1] 求下列函数的单调区间,并指出该函数在其单调区间上是增函数还是减函数.
(3)f(x)=-x2+2|x|+3
f(x)=-x2+2|x|+3=
根据解析式作函数图象如图所示,
函数f(x)的单调区间为
(-∞,-1],(-1,0),[0,1),[1,+∞).
f(x)在(-∞,-1],[0,1)上是增函数,
在(-1,0),[1,+∞)上是减函数.
求函数单调区间的方法
(1)利用基本初等函数的单调性,如本例(1)和(2),其中分段函数的单调区间要根据函数的自变量的取值范围分段求解;
(2)利用函数的图象,如本例(3).
注意:若所求出函数的单调增区间或单调减区间不唯一,函数的单调区间之间要用“,”隔开,如本例(3).
方法总结
跟踪训练
1.(1)根据如图所示,写出函数在每一单调区间上函数是增函数还是减函数.
函数在[-1,0],[2,4]上是减函数,在[0,2],[4,5]上是增函数.
跟踪训练
1.(2)写出y=|x2-2x-3|的单调区间.
f(x)=x2-2x-3, x< -1或x>3
f(x)= -(x2-2x-3), -1≤x ≤ 3
所以y=|x2-2x-3|的单调减区间为(-∞,-1],[1,3];单调增区间为[-1,1],[3,+∞).
题型二 函数单调性的判定与证明
[例2] 证明函数f(x)=x+ 在(0,1)上是减函数.
思路点拨:
设元0作差:f(x1)-f (x2)
判号:f(x1)>f (x2)
减函数
变形
结论
设x1,x2是区间(0,1)上的任意两个实数,且x1f(x1)-f(x2)=(x1+)- (x2+) =(x1-x2)+(-)
=(x1-x2)+ =(x1-x2)(1- )
=
∵0∴ >0,即f(x1)>f(x2),
∴f(x)=x+在(0,1)上是减函数.
[例2] 证明函数f(x)=x+在(0,1)上是减函数.
利用定义证明函数单调性的步骤
1 取值:设x1,x2是该区间内的任意两个值,且x1 2 作差变形:作差f x1 -f x2 ,并通过因式分解、通分、配方、有理化等手段,转化为易判断正负的式子.
3 定号:确定f x1 -f x2 的符号.
4 结论:根据f x1 -f x2 的符号及定义判断单调性.
关键点拨:作差变形是证明单调性的关键,且变形的结果是几个因式乘积的形式.
方法总结
跟踪训练
2.试用函数单调性的定义证明:f(x)= 在(1,+∞)上是减函数.
f(x)=2+,设x1>x2>1,
则f(x1)-f(x2)= -= ,
因为x1>x2>1,
所以x2-x1<0,x1-1>0,x2-1>0,
所以f(x1)所以f(x)在(1,+∞)上是减函数.
题型三 函数单调性的应用
[探究问题]
1.若函数f(x)是其定义域上的增函数,且f(a)>f(b),则a,b满足什么关系.如果函数f(x)是减函数呢?
提示:若函数f(x)是其定义域上的增函数,那么当f(a)>f(b)时,a>b;若函数f(x)是其定义域上的减函数,那么当f(a)>f(b)时,a题型三 函数单调性的应用
2.决定二次函数f(x)=ax2+bx+c单调性的因素有哪些?
提示:开口方向和对称轴的位置,即字母a的符号及-的大小.
[探究问题]
[例3] (1)若函数f(x)=-x2-2(a+1)x+3在区间(-∞,3]上是增函数,则实数a的取值范围是________.
分析f(x)的对称轴与区间的关系
数形结合
建立关于a的不等式
求a的范围
思路点拨
[例3] (1)若函数f(x)=-x2-2(a+1)x+3在区间(-∞,3]上是增函数,则实数a的取值范围是____________.
∵f(x)=-x2-2(a+1)x+3的开口向下,要使f(x)在(-∞,3]上是增函数,
只需-(a+1)≥3,即a≤-4.
∴实数a的取值范围为(-∞,-4]
(-∞,-4]
[例3] (2)已知函数y=f(x)是(-∞,+∞)上的增函数,且f(2x-3)>f(5x-6),则实数x的取值范围为________.
思路点拨
f(2x-3)>f(5x-6)
(-∞,+∞)上的增函数
建立关于x的不等式
求x的范围
[例3] (2)已知函数y=f(x)是(-∞,+∞)上的增函数,且f(2x-3)>f(5x-6),则实数x的取值范围为________.
∵f(x)在(-∞,+∞)上是增函数,且f(2x-3)>f(5x-6),
∴2x-3>5x-6,即x<1.
∴实数x的取值范围为(-∞,1).
(-∞,1)
多维探究
变式1 若函数f(x)=-x2-2(a+1)x+3在 (1,2)上是单调函数,求a的取值范围.
由题意可知-(a+1)≤1或-(a+1)≥2,即a≤-3或a≥-2.
所以a的取值范围为(-∞,-3]∪[-2,+∞).
变式2 已知函数y=f(x)是定义在(0,+∞)上的减函数,且f(2x-3)>f(5x-6),求x的范围.
由题意可知,
解得x> .
∴x的取值范围为(,+∞).
函数单调性的应用
1 函数单调性定义的“双向性”:利用定义可以判断、证明函数的单调性,反过来,若已知函数的单调性可以确定函数中参数的取值范围.
2 若一个函数在区间[a,b]上是单调的,则此函数在这一单调区间内的任意子集上也是单调的.
关键点拨
随堂检测
1.思考辨析
(1)所有的函数在其定义域上都具有单调性.( )
(2)若函数y=f(x)在区间[1,3]上是减函数,则函数y=f(x)的单调递减区间是[1,3].( )
(3)函数f(x)为R上的减函数,则f(-3)>f(3).( )
(4)若函数y=f(x)在定义域上有f(1)(5)若函数f(x)在(-∞,0)和(0,+∞)上单调递减,则f(x)在(-∞,0)∪(0,+∞)上单调递减.( )
×
×
√
×
×
2.如图是定义在区间[-5,5]上的函数y=f(x),则下列关于函数f(x)的说法错误的是( )
A.函数在区间[-5,-3]上单调递增
B.函数在区间[1,4]上单调递增
C.函数在区间[-3,1]∪[4,5]上单调递减
D.函数在区间[-5,5]上没有单调性
C
×
3.如果函数f(x)=x2-2bx+2在区间[3,+∞)上是增函数,则b的取值范围为( )
A.b=3 B.b≥3
C.b≤3 D.b≠3
函数f(x)=x2-2bx+2的图象是开口向上,
且以直线x=b为对称轴的抛物线,
若函数f(x)=x2-2bx+2在区间[3,+∞)上是增函数,则b≤3
C
4.证明:函数y=在(-1,+∞)上是增函数.
设x1>x2>-1,则
y1-y2=-= .
∵x1>x2>-1,∴x1-x2>0,x1+1>0,x2+1>0,
∴>0,即y1-y2>0,y1>y2,
∴y= 在(-1,+∞)上是增函数.
1.定义单调性时应强调x1,x2在其定义域内的任意性,其本质是把区间上无限多个函数值的大小比较转化为两个任意值的大小比较.
2.证明函数的单调性(利用定义)一定要严格遵循设元、作差、变形、 定号、结论的步骤,特别在变形上,一定要注意因式分解、配方等技巧的运用,直到符号判定水到渠成才可.
本课小结
3. 已知函数单调性求参数的范围时,要树立两种意识:
一是等价转化意识,
如f(x)在D上递增,则f(x1)二是数形结合意识,
如处理一(二)次函数及反比例函数中的含参数的范围问题.
本课小结
函数的单调性 (1)
本节目标
1.通过已学过的函数特别是二次函数,理解函数的单调性及其几何意义.
2.学会运用函数图象理解和研究函数的性质.
3.能够熟练应用定义判断与证明函数在某区间上的单调性.
本节目标
课前预习
(1)增函数、减函数的概念是什么?
(2)如何表示函数的单调区间?
(3)函数的单调性和单调区间有什么关系?
预习课本,思考并完成以下问题
课前小测
1.如果函数f(x)在[a,b]上是增函数,那么对于任意的x1,x2∈[a,b](x1≠x2),下列结论中不正确的是( )
A. >0 B.(x1-x2)[f(x1)-f(x2)]>0
C.f(a)
C
2.设f(x)=(2a-1)x+b在R上是减函数,则有( )
A.a≥ B.a≤
C.a>- D.a<
D
2a-1<0
a<
3.函数f(x)=2x2-mx+3,当x∈[-2,+∞)时,f(x)为增函数,当x∈(-∞,-2]时,函数f(x)为减函数,则m等于( )
A.-4 B.-8
C.8 D.无法确定
B
4.函数f(x)=|x-1|的单调递增区间是________,单调递减区间是________.
(-∞,1]
[1,+∞)
O
x
y
1
新知探究
定义域为I的函数f(x)的增减性
DI,对任意x1,x2∈D
分类
条件
结论
图示
减函数
增函数
x1
函数f(x)在区间D上是_______
f(x1)
增函数
减函数
定义中的x1,x2有以下3个特征
(1)任意性,即“任意取x1,x2”中“任意”二字绝不能去掉,证明时不能以特殊代替一般;
(2)有大小,通常规定x1
知识点睛
单调性与单调区间
如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间上具有(严格的) _________,区间D叫做y=f(x)的___________.
单调性
单调区间
一个函数出现两个或者两个以上的单调区间时,不能用“∪”连接,而应该用“和”连接.
如函数y=在(-∞,0)和(0,+∞)上单调递减,却不能表述为:函数y=在(-∞,0)∪(0,+∞)上单调递减.
易错提醒
题型突破
典例深度剖析 重点多维探究
题型一 求函数的单调区间
[例1] 求下列函数的单调区间,并指出该函数在其单调区间上是增函数还是减函数.
(1)f(x)=-;
(2)f(x)=
(3)f(x)=-x2+2|x|+3.
[例1] 求下列函数的单调区间,并指出该函数在其单调区间上是增函数还是减函数.
(1)f(x)=-;
函数f(x) =-的单调区间为(-∞,0),(0,+∞)
其在(-∞,0),(0,+∞)上都是增函数
[例1] 求下列函数的单调区间,并指出该函数在其单调区间上是增函数还是减函数.
(2)f(x)=
当x≥1时,f(x)是增函数,当x<1时,f(x)是减函数,
所以f(x)的单调区间为(-∞,1),[1,+∞),
并且函数f(x)在(-∞,1)上是减函数,在[1,+∞)上是增函数.
[例1] 求下列函数的单调区间,并指出该函数在其单调区间上是增函数还是减函数.
(3)f(x)=-x2+2|x|+3
f(x)=-x2+2|x|+3=
根据解析式作函数图象如图所示,
函数f(x)的单调区间为
(-∞,-1],(-1,0),[0,1),[1,+∞).
f(x)在(-∞,-1],[0,1)上是增函数,
在(-1,0),[1,+∞)上是减函数.
求函数单调区间的方法
(1)利用基本初等函数的单调性,如本例(1)和(2),其中分段函数的单调区间要根据函数的自变量的取值范围分段求解;
(2)利用函数的图象,如本例(3).
注意:若所求出函数的单调增区间或单调减区间不唯一,函数的单调区间之间要用“,”隔开,如本例(3).
方法总结
跟踪训练
1.(1)根据如图所示,写出函数在每一单调区间上函数是增函数还是减函数.
函数在[-1,0],[2,4]上是减函数,在[0,2],[4,5]上是增函数.
跟踪训练
1.(2)写出y=|x2-2x-3|的单调区间.
f(x)=x2-2x-3, x< -1或x>3
f(x)= -(x2-2x-3), -1≤x ≤ 3
所以y=|x2-2x-3|的单调减区间为(-∞,-1],[1,3];单调增区间为[-1,1],[3,+∞).
题型二 函数单调性的判定与证明
[例2] 证明函数f(x)=x+ 在(0,1)上是减函数.
思路点拨:
设元0
判号:f(x1)>f (x2)
减函数
变形
结论
设x1,x2是区间(0,1)上的任意两个实数,且x1
=(x1-x2)+ =(x1-x2)(1- )
=
∵0
∴f(x)=x+在(0,1)上是减函数.
[例2] 证明函数f(x)=x+在(0,1)上是减函数.
利用定义证明函数单调性的步骤
1 取值:设x1,x2是该区间内的任意两个值,且x1
3 定号:确定f x1 -f x2 的符号.
4 结论:根据f x1 -f x2 的符号及定义判断单调性.
关键点拨:作差变形是证明单调性的关键,且变形的结果是几个因式乘积的形式.
方法总结
跟踪训练
2.试用函数单调性的定义证明:f(x)= 在(1,+∞)上是减函数.
f(x)=2+,设x1>x2>1,
则f(x1)-f(x2)= -= ,
因为x1>x2>1,
所以x2-x1<0,x1-1>0,x2-1>0,
所以f(x1)
题型三 函数单调性的应用
[探究问题]
1.若函数f(x)是其定义域上的增函数,且f(a)>f(b),则a,b满足什么关系.如果函数f(x)是减函数呢?
提示:若函数f(x)是其定义域上的增函数,那么当f(a)>f(b)时,a>b;若函数f(x)是其定义域上的减函数,那么当f(a)>f(b)时,a
2.决定二次函数f(x)=ax2+bx+c单调性的因素有哪些?
提示:开口方向和对称轴的位置,即字母a的符号及-的大小.
[探究问题]
[例3] (1)若函数f(x)=-x2-2(a+1)x+3在区间(-∞,3]上是增函数,则实数a的取值范围是________.
分析f(x)的对称轴与区间的关系
数形结合
建立关于a的不等式
求a的范围
思路点拨
[例3] (1)若函数f(x)=-x2-2(a+1)x+3在区间(-∞,3]上是增函数,则实数a的取值范围是____________.
∵f(x)=-x2-2(a+1)x+3的开口向下,要使f(x)在(-∞,3]上是增函数,
只需-(a+1)≥3,即a≤-4.
∴实数a的取值范围为(-∞,-4]
(-∞,-4]
[例3] (2)已知函数y=f(x)是(-∞,+∞)上的增函数,且f(2x-3)>f(5x-6),则实数x的取值范围为________.
思路点拨
f(2x-3)>f(5x-6)
(-∞,+∞)上的增函数
建立关于x的不等式
求x的范围
[例3] (2)已知函数y=f(x)是(-∞,+∞)上的增函数,且f(2x-3)>f(5x-6),则实数x的取值范围为________.
∵f(x)在(-∞,+∞)上是增函数,且f(2x-3)>f(5x-6),
∴2x-3>5x-6,即x<1.
∴实数x的取值范围为(-∞,1).
(-∞,1)
多维探究
变式1 若函数f(x)=-x2-2(a+1)x+3在 (1,2)上是单调函数,求a的取值范围.
由题意可知-(a+1)≤1或-(a+1)≥2,即a≤-3或a≥-2.
所以a的取值范围为(-∞,-3]∪[-2,+∞).
变式2 已知函数y=f(x)是定义在(0,+∞)上的减函数,且f(2x-3)>f(5x-6),求x的范围.
由题意可知,
解得x> .
∴x的取值范围为(,+∞).
函数单调性的应用
1 函数单调性定义的“双向性”:利用定义可以判断、证明函数的单调性,反过来,若已知函数的单调性可以确定函数中参数的取值范围.
2 若一个函数在区间[a,b]上是单调的,则此函数在这一单调区间内的任意子集上也是单调的.
关键点拨
随堂检测
1.思考辨析
(1)所有的函数在其定义域上都具有单调性.( )
(2)若函数y=f(x)在区间[1,3]上是减函数,则函数y=f(x)的单调递减区间是[1,3].( )
(3)函数f(x)为R上的减函数,则f(-3)>f(3).( )
(4)若函数y=f(x)在定义域上有f(1)
×
×
√
×
×
2.如图是定义在区间[-5,5]上的函数y=f(x),则下列关于函数f(x)的说法错误的是( )
A.函数在区间[-5,-3]上单调递增
B.函数在区间[1,4]上单调递增
C.函数在区间[-3,1]∪[4,5]上单调递减
D.函数在区间[-5,5]上没有单调性
C
×
3.如果函数f(x)=x2-2bx+2在区间[3,+∞)上是增函数,则b的取值范围为( )
A.b=3 B.b≥3
C.b≤3 D.b≠3
函数f(x)=x2-2bx+2的图象是开口向上,
且以直线x=b为对称轴的抛物线,
若函数f(x)=x2-2bx+2在区间[3,+∞)上是增函数,则b≤3
C
4.证明:函数y=在(-1,+∞)上是增函数.
设x1>x2>-1,则
y1-y2=-= .
∵x1>x2>-1,∴x1-x2>0,x1+1>0,x2+1>0,
∴>0,即y1-y2>0,y1>y2,
∴y= 在(-1,+∞)上是增函数.
1.定义单调性时应强调x1,x2在其定义域内的任意性,其本质是把区间上无限多个函数值的大小比较转化为两个任意值的大小比较.
2.证明函数的单调性(利用定义)一定要严格遵循设元、作差、变形、 定号、结论的步骤,特别在变形上,一定要注意因式分解、配方等技巧的运用,直到符号判定水到渠成才可.
本课小结
3. 已知函数单调性求参数的范围时,要树立两种意识:
一是等价转化意识,
如f(x)在D上递增,则f(x1)
如处理一(二)次函数及反比例函数中的含参数的范围问题.
本课小结
