人教B版(2019)数学必修第一册 3_1_3函数的奇偶性(1)课件(共42张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册 3_1_3函数的奇偶性(1)课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 22:07:04 | ||
图片预览











文档简介
(共42张PPT)
函数的奇偶性(1)
1. 理解奇函数、偶函数的定义.
2.了解奇函数、偶函数图象的特征.
3.掌握判断函数奇偶性的方法.
本节目标
课前预习
(1)偶函数与奇函数的定义分别是什么?
(2)奇、偶函数的定义域有什么特点?
(3)奇、偶函数的图象分别有什么特征?
预习课本,思考并完成以下问题
课前小测
1.下列函数是偶函数的是( )
A.y=x B.y=2x2-3
C.y= D.y=x2,x∈[0,1]
B
定义域不关于原点对称
定义域不关于原点对称
奇函数
√
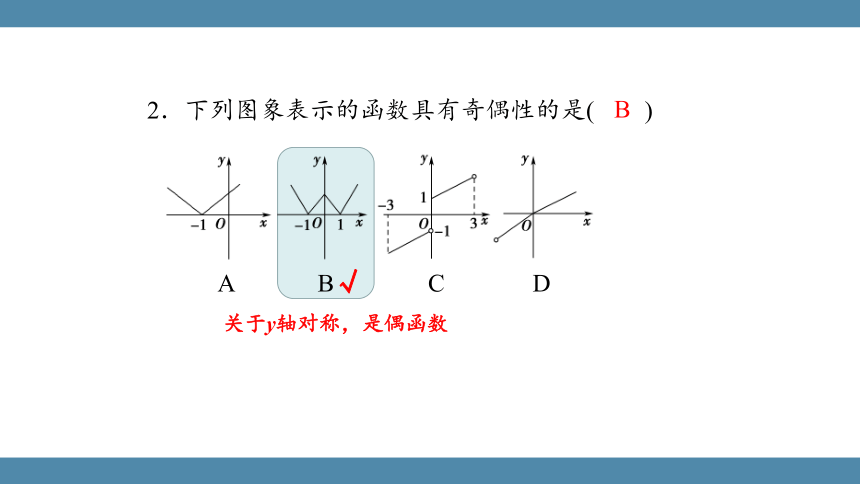
2.下列图象表示的函数具有奇偶性的是( )
A B C D
关于y轴对称,是偶函数
√
B
3.函数y=f(x),x∈[-1,a](a>-1)是奇函数,则a等于( )
A.-1 B.0
C.1 D.无法确定
∵奇函数的定义域关于原点对称
∴a-1=0,即a=1.
C
4.若f(x)为R上的偶函数,且f(2)=3,则f(-2)=________.
∵f(x)为R上的偶函数
∴f(-2)=f(2)=3.
3
新知探究
函数的奇偶性
奇偶性 偶函数 奇函数
条件 设函数f(x)的定义域为I,如果 x∈I,都有-x∈I 结论 f(-x)=f(x) f(-x)=-f(x)
图象特点 关于_______对称 关于______对称
y轴
原点
思考:具有奇偶性的函数,其定义域有何特点?
提示:定义域关于原点对称.
题型突破
典例深度剖析 重点多维探究
题型一 函数奇偶性的判断
[例1] 判断下列函数的奇偶性:
(1) f(x)=x3+x; (2) f(x)= + ;
(3) f(x)= ; (4) f(x)=
题型一 函数奇偶性的判断
[例1] 判断下列函数的奇偶性:
(1) f(x)=x3+x
函数的定义域为R,关于原点对称
f(-x)=(-x)3+(-x)=-(x3+x)=-f(x)
因此函数f(x)是奇函数
题型一 函数奇偶性的判断
[例1] 判断下列函数的奇偶性:
(2) f(x)= +
由得x2=1,即x=±1.
因此函数的定义域为{-1,1},关于原点对称.
又f(1)=f(-1)=-f(-1)=0,
所以f(x)既是奇函数又是偶函数.
题型一 函数奇偶性的判断
[例1] 判断下列函数的奇偶性:
(3) f(x)=
函数f(x)的定义域是(-∞,-1)∪(-1,+∞),
不关于原点对称,
所以f(x)既不是奇函数也不是偶函数.
f(-x)=
(4) f(x)=
题型一 函数奇偶性的判断
[例1] 判断下列函数的奇偶性:
函数f(x)的定义域为R,关于原点对称.
即f(-x)=
于是有f(-x)=-f(x).所以f(x)为奇函数.
判断函数奇偶性的两种方法
定义法
图象法
方法总结
跟踪训练
1.下列函数中,是偶函数的有________.(填序号)
①f(x)=x3; ②f(x)=|x|+1; ③f(x)= ;
④f(x)=x+; ⑤f(x)=x2,x∈[-1,2].
②③
奇函数
偶函数
偶函数
奇函数
非奇非偶函数
题型二 奇偶函数的图象问题
[例2] 已知奇函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示.
(1)画出在区间[-5,0]上的图象;
(2)写出使f(x)<0的x的取值集合.
[例2] 已知奇函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示.
(1)画出在区间[-5,0]上的图象;
(2)写出使f(x)<0的x的取值集合.
由图象知,使函数值y<0的x的取值集合为(-2,0)∪(2,5).
变式 已知偶函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示.
多维探究
(1)画出在区间[-5,0]上的图象;
(2)写出使f(x)<0的x的取值集合.
变式 已知偶函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示.
(1)画出在区间[-5,0]上的图象;
(2)写出使f(x)<0的x的取值集合.
使函数值y<0的x的取值集合为(-5,-2)∪(2,5).
根据奇、偶函数图象的对称性可以解决诸如求函数值或画出奇偶函数图象的问题.
巧用奇、偶函数的图象求解问题
依据
奇函数 图象关于原点对称,
偶函数 图象关于y轴对称.
求解
方法技巧
跟踪训练
2.如图是函数f(x)= 在区间[0,+∞)上的图象,请据此在该坐标系中补全函数f(x)在定义域内的图象,请说明你的作图依据.
2.如图是函数f(x)= 在区间[0,+∞)上的图象,请据此在该坐标系中补全函数f(x)在定义域内的图象,请说明你的作图依据.
因为f(x)=,所以f(x)的定义域为R.
又对任意x∈R,都有f(-x)= ==f(x),
所以f(x)为偶函数.所以f(x)的图象关于y轴对称,其图象如图所示.
题型三 利用函数的奇偶性求值
[探究问题]
1.对于定义域内的任意x,若f(-x)+f(x)=0,则函数f(x)是否具有奇偶性?若f(-x)-f(x)=0呢?
提示:由f(-x)+f(x)=0得f(-x)=-f(x),
∴f(x)为奇函数.
由f(-x)-f(x)=0得f(-x)=f(x),
∴f(x)为偶函数.
2.若f(x)是奇函数且在x=0处有定义,则f(0)的值可求吗?若f(x)为偶函数呢?
提示:若f(x)为奇函数,则f(0)=0;若f(x)为偶函数,无法求出f(0)的值.
[探究问题]
[例3] (1)若函数f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a=________,b=________;
f(x)是偶函数
定义域关于原点对称
求a的值
图象关于y轴对称
求b的值
思路点拨
[例3] (1)若函数f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a=________,b=________;
因为偶函数的定义域关于原点对称,
所以a-1=-2a,解得a=.
又函数f(x)= x2+bx+b+1为二次函数,
结合偶函数图象的特点,易得b=0.
0
[例3] (2)已知f(x)=x7-ax5+bx3+cx+2,若f(-3)=-3,则f(3)=________.
思路点拨
g(x)=x7-ax5+bx3+cx
判断g(x)的奇偶性
计算g(-3)
代入求f(3)
[例3] (2)已知f(x)=x7-ax5+bx3+cx+2,若f(-3)=-3,则f(3)=________.
令g(x)=x7-ax5+bx3+cx,则g(x)是奇函数,
∴f(-3)=g(-3)+2=-g(3)+2,
又f(-3)=-3,
∴g(3)=5.
又f(3)=g(3)+2,
所以f(3)=5+2=7.
7
根据f -x =-f x 或f -x =f x 列式,比较系数即可求解.
利用奇偶性求参数的常见类型及策略
定义域含参数
奇、偶函数f x 的定义域为[a,b],根据定义域关于原点对称,利用a+b=0求参数.
解析式含参数
解题策略
跟踪训练
3.若f(x)=(x+a)(x-4)为偶函数,则实数a=________.
f(x)=(x+a)(x-4)=x2+(a-4)x-4a,
f(-x)=(-x+a)(-x-4)=x2-(a-4)x-4a,两式恒相等,则a-4=0,即a=4.
4
方法一
跟踪训练
3.若f(x)=(x+a)(x-4)为偶函数,则实数a=________.
4
方法二
f(x)=(x+a)(x-4)=x2+(a-4)x-4a,
要使函数为偶函数,只需多项式的奇次项系数为0,
即a-4=0,则a=4.
跟踪训练
3.若f(x)=(x+a)(x-4)为偶函数,则实数a=________.
4
方法三
根据二次函数的奇偶性可知,形如f(x)=ax2+c的都是偶函数,因而本题只需将解析式看成是平方差公式,则a=4.
随堂检测
1.思考辨析
(1)函数f(x)=x2,x∈[0,+∞)是偶函数.( )
(2)对于函数y=f(x),若存在x,使f(-x)=-f(x),则函数y=f(x)一定是奇函数.( )
(3)不存在既是奇函数,又是偶函数的函数.( )
(4)若函数的定义域关于原点对称,则这个函数不是奇函数就是偶函数.( )
×
×
×
×
2.函数f(x)=|x|+1是( )
A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.非奇非偶函数
B
∵f(-x)=|-x|+1=|x|+1=f(x),
∴f(x)为偶函数.
3.已知函数f(x)=ax2+2x是奇函数,则实数a=______.
∵f(x)为奇函数,
∴f(-x)+f(x)=0,
∴2ax2=0对任意x∈R恒成立,所以a=0.
0
4.已知函数y=f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示.
(1)请补出完整函数y=f(x)的图象;
(2)根据图象写出函数y=f(x)的增区间;
(3)根据图象写出使f(x)<0的x的取值集合.
单调增区间为(-1,0),(1,+∞)
(-2,0)∪(0,2)
1.奇偶性是函数“整体”性质,只有对函数f(x)定义域内的每一个值x,都有f(-x)=-f(x)(或f(-x)=f(x)),才能说f(x)是奇函数(或偶函数).
2.函数的奇偶性是其相应图象特殊对称性的反映,也体现了在关于原点对称的定义域的两个区间上函数值及其性质的相互转化,这是对称思想的应用.
本课小结
通过本节课,你学会了什么?
函数的奇偶性(1)
1. 理解奇函数、偶函数的定义.
2.了解奇函数、偶函数图象的特征.
3.掌握判断函数奇偶性的方法.
本节目标
课前预习
(1)偶函数与奇函数的定义分别是什么?
(2)奇、偶函数的定义域有什么特点?
(3)奇、偶函数的图象分别有什么特征?
预习课本,思考并完成以下问题
课前小测
1.下列函数是偶函数的是( )
A.y=x B.y=2x2-3
C.y= D.y=x2,x∈[0,1]
B
定义域不关于原点对称
定义域不关于原点对称
奇函数
√
2.下列图象表示的函数具有奇偶性的是( )
A B C D
关于y轴对称,是偶函数
√
B
3.函数y=f(x),x∈[-1,a](a>-1)是奇函数,则a等于( )
A.-1 B.0
C.1 D.无法确定
∵奇函数的定义域关于原点对称
∴a-1=0,即a=1.
C
4.若f(x)为R上的偶函数,且f(2)=3,则f(-2)=________.
∵f(x)为R上的偶函数
∴f(-2)=f(2)=3.
3
新知探究
函数的奇偶性
奇偶性 偶函数 奇函数
条件 设函数f(x)的定义域为I,如果 x∈I,都有-x∈I 结论 f(-x)=f(x) f(-x)=-f(x)
图象特点 关于_______对称 关于______对称
y轴
原点
思考:具有奇偶性的函数,其定义域有何特点?
提示:定义域关于原点对称.
题型突破
典例深度剖析 重点多维探究
题型一 函数奇偶性的判断
[例1] 判断下列函数的奇偶性:
(1) f(x)=x3+x; (2) f(x)= + ;
(3) f(x)= ; (4) f(x)=
题型一 函数奇偶性的判断
[例1] 判断下列函数的奇偶性:
(1) f(x)=x3+x
函数的定义域为R,关于原点对称
f(-x)=(-x)3+(-x)=-(x3+x)=-f(x)
因此函数f(x)是奇函数
题型一 函数奇偶性的判断
[例1] 判断下列函数的奇偶性:
(2) f(x)= +
由得x2=1,即x=±1.
因此函数的定义域为{-1,1},关于原点对称.
又f(1)=f(-1)=-f(-1)=0,
所以f(x)既是奇函数又是偶函数.
题型一 函数奇偶性的判断
[例1] 判断下列函数的奇偶性:
(3) f(x)=
函数f(x)的定义域是(-∞,-1)∪(-1,+∞),
不关于原点对称,
所以f(x)既不是奇函数也不是偶函数.
f(-x)=
(4) f(x)=
题型一 函数奇偶性的判断
[例1] 判断下列函数的奇偶性:
函数f(x)的定义域为R,关于原点对称.
即f(-x)=
于是有f(-x)=-f(x).所以f(x)为奇函数.
判断函数奇偶性的两种方法
定义法
图象法
方法总结
跟踪训练
1.下列函数中,是偶函数的有________.(填序号)
①f(x)=x3; ②f(x)=|x|+1; ③f(x)= ;
④f(x)=x+; ⑤f(x)=x2,x∈[-1,2].
②③
奇函数
偶函数
偶函数
奇函数
非奇非偶函数
题型二 奇偶函数的图象问题
[例2] 已知奇函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示.
(1)画出在区间[-5,0]上的图象;
(2)写出使f(x)<0的x的取值集合.
[例2] 已知奇函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示.
(1)画出在区间[-5,0]上的图象;
(2)写出使f(x)<0的x的取值集合.
由图象知,使函数值y<0的x的取值集合为(-2,0)∪(2,5).
变式 已知偶函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示.
多维探究
(1)画出在区间[-5,0]上的图象;
(2)写出使f(x)<0的x的取值集合.
变式 已知偶函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示.
(1)画出在区间[-5,0]上的图象;
(2)写出使f(x)<0的x的取值集合.
使函数值y<0的x的取值集合为(-5,-2)∪(2,5).
根据奇、偶函数图象的对称性可以解决诸如求函数值或画出奇偶函数图象的问题.
巧用奇、偶函数的图象求解问题
依据
奇函数 图象关于原点对称,
偶函数 图象关于y轴对称.
求解
方法技巧
跟踪训练
2.如图是函数f(x)= 在区间[0,+∞)上的图象,请据此在该坐标系中补全函数f(x)在定义域内的图象,请说明你的作图依据.
2.如图是函数f(x)= 在区间[0,+∞)上的图象,请据此在该坐标系中补全函数f(x)在定义域内的图象,请说明你的作图依据.
因为f(x)=,所以f(x)的定义域为R.
又对任意x∈R,都有f(-x)= ==f(x),
所以f(x)为偶函数.所以f(x)的图象关于y轴对称,其图象如图所示.
题型三 利用函数的奇偶性求值
[探究问题]
1.对于定义域内的任意x,若f(-x)+f(x)=0,则函数f(x)是否具有奇偶性?若f(-x)-f(x)=0呢?
提示:由f(-x)+f(x)=0得f(-x)=-f(x),
∴f(x)为奇函数.
由f(-x)-f(x)=0得f(-x)=f(x),
∴f(x)为偶函数.
2.若f(x)是奇函数且在x=0处有定义,则f(0)的值可求吗?若f(x)为偶函数呢?
提示:若f(x)为奇函数,则f(0)=0;若f(x)为偶函数,无法求出f(0)的值.
[探究问题]
[例3] (1)若函数f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a=________,b=________;
f(x)是偶函数
定义域关于原点对称
求a的值
图象关于y轴对称
求b的值
思路点拨
[例3] (1)若函数f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a=________,b=________;
因为偶函数的定义域关于原点对称,
所以a-1=-2a,解得a=.
又函数f(x)= x2+bx+b+1为二次函数,
结合偶函数图象的特点,易得b=0.
0
[例3] (2)已知f(x)=x7-ax5+bx3+cx+2,若f(-3)=-3,则f(3)=________.
思路点拨
g(x)=x7-ax5+bx3+cx
判断g(x)的奇偶性
计算g(-3)
代入求f(3)
[例3] (2)已知f(x)=x7-ax5+bx3+cx+2,若f(-3)=-3,则f(3)=________.
令g(x)=x7-ax5+bx3+cx,则g(x)是奇函数,
∴f(-3)=g(-3)+2=-g(3)+2,
又f(-3)=-3,
∴g(3)=5.
又f(3)=g(3)+2,
所以f(3)=5+2=7.
7
根据f -x =-f x 或f -x =f x 列式,比较系数即可求解.
利用奇偶性求参数的常见类型及策略
定义域含参数
奇、偶函数f x 的定义域为[a,b],根据定义域关于原点对称,利用a+b=0求参数.
解析式含参数
解题策略
跟踪训练
3.若f(x)=(x+a)(x-4)为偶函数,则实数a=________.
f(x)=(x+a)(x-4)=x2+(a-4)x-4a,
f(-x)=(-x+a)(-x-4)=x2-(a-4)x-4a,两式恒相等,则a-4=0,即a=4.
4
方法一
跟踪训练
3.若f(x)=(x+a)(x-4)为偶函数,则实数a=________.
4
方法二
f(x)=(x+a)(x-4)=x2+(a-4)x-4a,
要使函数为偶函数,只需多项式的奇次项系数为0,
即a-4=0,则a=4.
跟踪训练
3.若f(x)=(x+a)(x-4)为偶函数,则实数a=________.
4
方法三
根据二次函数的奇偶性可知,形如f(x)=ax2+c的都是偶函数,因而本题只需将解析式看成是平方差公式,则a=4.
随堂检测
1.思考辨析
(1)函数f(x)=x2,x∈[0,+∞)是偶函数.( )
(2)对于函数y=f(x),若存在x,使f(-x)=-f(x),则函数y=f(x)一定是奇函数.( )
(3)不存在既是奇函数,又是偶函数的函数.( )
(4)若函数的定义域关于原点对称,则这个函数不是奇函数就是偶函数.( )
×
×
×
×
2.函数f(x)=|x|+1是( )
A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.非奇非偶函数
B
∵f(-x)=|-x|+1=|x|+1=f(x),
∴f(x)为偶函数.
3.已知函数f(x)=ax2+2x是奇函数,则实数a=______.
∵f(x)为奇函数,
∴f(-x)+f(x)=0,
∴2ax2=0对任意x∈R恒成立,所以a=0.
0
4.已知函数y=f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示.
(1)请补出完整函数y=f(x)的图象;
(2)根据图象写出函数y=f(x)的增区间;
(3)根据图象写出使f(x)<0的x的取值集合.
单调增区间为(-1,0),(1,+∞)
(-2,0)∪(0,2)
1.奇偶性是函数“整体”性质,只有对函数f(x)定义域内的每一个值x,都有f(-x)=-f(x)(或f(-x)=f(x)),才能说f(x)是奇函数(或偶函数).
2.函数的奇偶性是其相应图象特殊对称性的反映,也体现了在关于原点对称的定义域的两个区间上函数值及其性质的相互转化,这是对称思想的应用.
本课小结
通过本节课,你学会了什么?
