人教B版(2019)数学必修第一册综合复习:函数的概念及其表示课件(共37张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册综合复习:函数的概念及其表示课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 731.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 00:00:00 | ||
图片预览










文档简介
(共37张PPT)
函数的概念及表示
新课程标准 考向预测 1.通过实例,体会函数是描述变量之间的依赖关系的重要数学模型,学会用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;了解构成函数的要素,会求一些简单函数的定义域和值域. 命题角度 1.函数的定义域
2.求函数的解析式
3.分段函数
2.会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数. 3.通过具体实例,了解简单的分段函数,并能简单应用. 核心素养 数学抽象数学运算
基础梳理
1.函数的概念
设A,B都是非空的_____,如果按照某种确定的对应关系f,使对于集合A中的_____一个数x,在集合B中都有_________的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),x∈A.
数集
任意
唯一确定
一、函数及其概念
2.函数的定义域、值域
在函数y=f(x),x∈A中,x叫做自变量,x的取值范围A叫做函数的________;与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的________.
定义域
值域
求函数定义域的策略
(1)确定函数的定义域常从解析式本身有意义,或从实际出发.
(2)如果函数y=f(x)是用表格给出,则表格中x的集合即为定义域.
(3)如果函数y=f(x)是用图象给出,则图象在x轴上的投影所覆盖的x的集合即为定义域.
方法策略
1.基本表示方法:①________、②________、③________.
2.分段函数:在定义域的不同范围内函数具有不同的解析式,这类函数称为__________.分段函数是一个函数,分段函数的定义域是各段定义域的______,值域是各段值域的________.
解析法
图象法
列表法
分段函数
并集
并集
二、函数的表示法
关于分段函数的3个注意
(1)分段函数虽然由几个部分构成,但它表示同一个函数.
(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集.
(3)各段函数的定义域不可以相交.
方法策略
1.若函数y=f(x)的定义域为M={x|-2≤x≤2},值域为N={y|0≤y≤2},则函数y=f(x)的图象可能是( )
B
基础小测
A
B
C
D
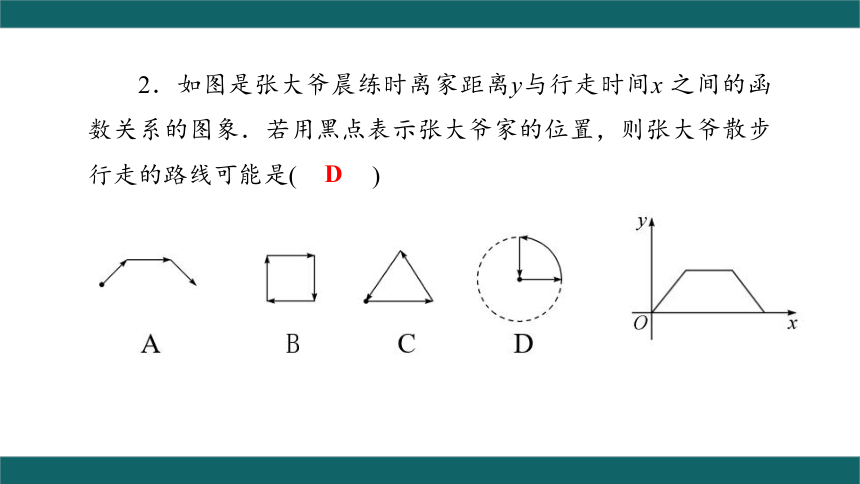
2.如图是张大爷晨练时离家距离y与行走时间x 之间的函数关系的图象.若用黑点表示张大爷家的位置,则张大爷散步行走的路线可能是( )
D
3.(2020届“四省八校”第一次质检)设函数f(x)= ,则f(-3)的值为( )
A. B.2 C. D.8
B
±1
4.设函数f(x)= ,若f(a)+f(-1)=2,则a=________.
考点突破
[例1] (2020届湖南常德一中高三月考)下列函数中,与函数y=x+1是相等函数的是( )
A.y=()2 B.y= +1
C.y= +1 D.y= +1
B
考点一 函数的概念(高考热度:★)
B
[例2] 下列所给图象是函数图象的个数为( )
① ② ③ ④
A.1 B.2 C.3 D.4
方法技巧
任何一个自变量只能对应一个函数值.
1.两个函数是不是同一个函数,取决于它们的定义域和对应关系是否分别相同,只有当两个函数的定义域和对应关系均完全相同时,才表示同一函数.另外,函数的自变量习惯上用x表示,但也可用其他字母表示,如: f(x)=2x-1,g(t)=2t-1,h(m)=2m-1均表示同一函数.
解题通法
2.函数概念中要特别注意:定义域中的任何一个自变量只能对应唯一确定的一个函数值,这是函数图象与一般曲线不同的地方.
解题通法
考点二 函数的定义域(高考热度:★★)
考向1 求具体函数的定义域
[例3] (2020届五省创优名校上学期第二次联考)函数f(x)= -ln(4-x2)的定义域是( )
A.[-1,2) B.(-2,2)
C.(-1,2) D.(-2,-1)∪(-1,2)
C
[例4] (2019江苏卷,4)函数y= 的定义域是____________.
[-1,7]
常见函数定义域的类型
解题通法
[例5]已知函数f(x)的定义域为(-1,0),则函数f(2x+1)的定义域为( )
A.(-1,1) B.(-1,-)
C.(-1,0) D.(,1)
B
考向2 求抽象函数的定义域
求抽象函数定义域的方法
[变式1] 函数f(2x+1)的定义域为(-1,0),则函数f(x)的定义域为________.
(-1,1)
对点变式
[变式2] 函数f(2x+1)的定义域为(-1,0),则函数f(2x-1)的定义域为________.
(0,1)
考向3 已知函数的定义域求参数的值(范围)
[例6] 若函数y= 的定义域为R,则实数m的取值范围是 ( )
A. B.
C. D.
D
已知函数的定义域求参数的值或范围,可将问题转化成含参数的不等式或方程,然后求解.
解题技法
考点三 求函数的解析式(高考热度:★)
1.已知f(+1)=lg x,则f(x)=_____________.
2.已知f(x)是二次函数且f(0)=2, f(x+1)-f(x)=x-1,则f(x)=____________.
3.(2020届广西南宁一中高三月考)已知函数f(x)的定义域为(0,+∞),且f(x)=2f()· -1,则f(x)=___________.
求函数解析式的4种方法及适用条件
(1)待定系数法
先设出含有待定系数的解析式,再利用恒等式的性质,或将已知条件代入,建立方程(组),通过解方程(组)求出相应的待定系数.
(2)换元法
对于形如y=f(g(x))的函数解析式,令t=g(x),从中求出x=φ(t),然后代入表达式求出f(t),再将t换成x,得到f(x)的解析式,要注意新元的取值范围.
求函数解析式的4种方法及适用条件
(3)配凑法
由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),便得f(x)的解析式.
(4)解方程组法
已知关于f(x)与f或f(-x)的表达式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出f(x).
D
考点四 分段函数(高考热度:★★★)
考向1 分段函数求值
1.设函数f(x)= 若f(f())=2,则实数a为( )
A.- B.- C. D.
2.(2020届贵州遵义第一中学高三月考)已知函数f(x)= , 则f(f(3))=________.
2
求分段函数的函数值的步骤
(1)先确定要求值的自变量属于哪一个区间.
(2)然后代入相应的函数解析式求值,直到求出具体值为止.
[注意]
①自变量的值不确定时,必须分类讨论;
②求值时注意函数奇偶性、周期性的应用;
③出现f(f(a))求值形式时,应由内到外逐层求值.
考向2 求参数或自变量的值(或范围)
1.已知函数f(x)= ,若f(a)+f(1)=0,则实数a=________.
-3
2.设函数f(x)= ,则f(f(0))=_____,若f(m)>1,则实数m的取值范围是_______________________.
0
(-∞,0)∪(e,+∞)
分段函数中,已知函数值(或范围)求自变量的值(或范围)的方法
(1)根据每一段的解析式分别求解,但要注意检验所求自变量的值(或范围)是否符合相应段的自变量的取值范围,最后将各段的结果合起来(求并集)即可;
(2)如果分段函数的图象易得,也在可以画出函数图象后结合图象求解.
方法总结
通过本节课,你学会了什么?
函数的概念及表示
新课程标准 考向预测 1.通过实例,体会函数是描述变量之间的依赖关系的重要数学模型,学会用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;了解构成函数的要素,会求一些简单函数的定义域和值域. 命题角度 1.函数的定义域
2.求函数的解析式
3.分段函数
2.会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数. 3.通过具体实例,了解简单的分段函数,并能简单应用. 核心素养 数学抽象数学运算
基础梳理
1.函数的概念
设A,B都是非空的_____,如果按照某种确定的对应关系f,使对于集合A中的_____一个数x,在集合B中都有_________的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),x∈A.
数集
任意
唯一确定
一、函数及其概念
2.函数的定义域、值域
在函数y=f(x),x∈A中,x叫做自变量,x的取值范围A叫做函数的________;与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的________.
定义域
值域
求函数定义域的策略
(1)确定函数的定义域常从解析式本身有意义,或从实际出发.
(2)如果函数y=f(x)是用表格给出,则表格中x的集合即为定义域.
(3)如果函数y=f(x)是用图象给出,则图象在x轴上的投影所覆盖的x的集合即为定义域.
方法策略
1.基本表示方法:①________、②________、③________.
2.分段函数:在定义域的不同范围内函数具有不同的解析式,这类函数称为__________.分段函数是一个函数,分段函数的定义域是各段定义域的______,值域是各段值域的________.
解析法
图象法
列表法
分段函数
并集
并集
二、函数的表示法
关于分段函数的3个注意
(1)分段函数虽然由几个部分构成,但它表示同一个函数.
(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集.
(3)各段函数的定义域不可以相交.
方法策略
1.若函数y=f(x)的定义域为M={x|-2≤x≤2},值域为N={y|0≤y≤2},则函数y=f(x)的图象可能是( )
B
基础小测
A
B
C
D
2.如图是张大爷晨练时离家距离y与行走时间x 之间的函数关系的图象.若用黑点表示张大爷家的位置,则张大爷散步行走的路线可能是( )
D
3.(2020届“四省八校”第一次质检)设函数f(x)= ,则f(-3)的值为( )
A. B.2 C. D.8
B
±1
4.设函数f(x)= ,若f(a)+f(-1)=2,则a=________.
考点突破
[例1] (2020届湖南常德一中高三月考)下列函数中,与函数y=x+1是相等函数的是( )
A.y=()2 B.y= +1
C.y= +1 D.y= +1
B
考点一 函数的概念(高考热度:★)
B
[例2] 下列所给图象是函数图象的个数为( )
① ② ③ ④
A.1 B.2 C.3 D.4
方法技巧
任何一个自变量只能对应一个函数值.
1.两个函数是不是同一个函数,取决于它们的定义域和对应关系是否分别相同,只有当两个函数的定义域和对应关系均完全相同时,才表示同一函数.另外,函数的自变量习惯上用x表示,但也可用其他字母表示,如: f(x)=2x-1,g(t)=2t-1,h(m)=2m-1均表示同一函数.
解题通法
2.函数概念中要特别注意:定义域中的任何一个自变量只能对应唯一确定的一个函数值,这是函数图象与一般曲线不同的地方.
解题通法
考点二 函数的定义域(高考热度:★★)
考向1 求具体函数的定义域
[例3] (2020届五省创优名校上学期第二次联考)函数f(x)= -ln(4-x2)的定义域是( )
A.[-1,2) B.(-2,2)
C.(-1,2) D.(-2,-1)∪(-1,2)
C
[例4] (2019江苏卷,4)函数y= 的定义域是____________.
[-1,7]
常见函数定义域的类型
解题通法
[例5]已知函数f(x)的定义域为(-1,0),则函数f(2x+1)的定义域为( )
A.(-1,1) B.(-1,-)
C.(-1,0) D.(,1)
B
考向2 求抽象函数的定义域
求抽象函数定义域的方法
[变式1] 函数f(2x+1)的定义域为(-1,0),则函数f(x)的定义域为________.
(-1,1)
对点变式
[变式2] 函数f(2x+1)的定义域为(-1,0),则函数f(2x-1)的定义域为________.
(0,1)
考向3 已知函数的定义域求参数的值(范围)
[例6] 若函数y= 的定义域为R,则实数m的取值范围是 ( )
A. B.
C. D.
D
已知函数的定义域求参数的值或范围,可将问题转化成含参数的不等式或方程,然后求解.
解题技法
考点三 求函数的解析式(高考热度:★)
1.已知f(+1)=lg x,则f(x)=_____________.
2.已知f(x)是二次函数且f(0)=2, f(x+1)-f(x)=x-1,则f(x)=____________.
3.(2020届广西南宁一中高三月考)已知函数f(x)的定义域为(0,+∞),且f(x)=2f()· -1,则f(x)=___________.
求函数解析式的4种方法及适用条件
(1)待定系数法
先设出含有待定系数的解析式,再利用恒等式的性质,或将已知条件代入,建立方程(组),通过解方程(组)求出相应的待定系数.
(2)换元法
对于形如y=f(g(x))的函数解析式,令t=g(x),从中求出x=φ(t),然后代入表达式求出f(t),再将t换成x,得到f(x)的解析式,要注意新元的取值范围.
求函数解析式的4种方法及适用条件
(3)配凑法
由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),便得f(x)的解析式.
(4)解方程组法
已知关于f(x)与f或f(-x)的表达式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出f(x).
D
考点四 分段函数(高考热度:★★★)
考向1 分段函数求值
1.设函数f(x)= 若f(f())=2,则实数a为( )
A.- B.- C. D.
2.(2020届贵州遵义第一中学高三月考)已知函数f(x)= , 则f(f(3))=________.
2
求分段函数的函数值的步骤
(1)先确定要求值的自变量属于哪一个区间.
(2)然后代入相应的函数解析式求值,直到求出具体值为止.
[注意]
①自变量的值不确定时,必须分类讨论;
②求值时注意函数奇偶性、周期性的应用;
③出现f(f(a))求值形式时,应由内到外逐层求值.
考向2 求参数或自变量的值(或范围)
1.已知函数f(x)= ,若f(a)+f(1)=0,则实数a=________.
-3
2.设函数f(x)= ,则f(f(0))=_____,若f(m)>1,则实数m的取值范围是_______________________.
0
(-∞,0)∪(e,+∞)
分段函数中,已知函数值(或范围)求自变量的值(或范围)的方法
(1)根据每一段的解析式分别求解,但要注意检验所求自变量的值(或范围)是否符合相应段的自变量的取值范围,最后将各段的结果合起来(求并集)即可;
(2)如果分段函数的图象易得,也在可以画出函数图象后结合图象求解.
方法总结
通过本节课,你学会了什么?
