人教B版(2019)数学必修第一册综合复习:函数的奇偶性及周期性课件(共39张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册综合复习:函数的奇偶性及周期性课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 801.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 00:00:00 | ||
图片预览










文档简介
(共39张PPT)
函数的奇偶性及周期性
考纲分析
课程标准解读 关联考点 核心素养
1.结合具体函数,了解函数奇偶性的含义. 2.会运用函数图象理解和研究函数的奇偶性. 3.了解函数周期性、最小正周期的含义,会判断、应用简单函数的周期性. 1.函数的奇偶性. 2.函数的周期性. 3.函数性质的综合应用. 1.数学抽象.
2.逻辑推理.
3.数学运算.
课前自测
1.判断正误(正确的打“√”,错误的打“×”)
(1)若f(x)是定义在R上的奇函数,则f(-x)+f(x)=0.( )
(2)偶函数的图象不一定过原点,奇函数的图象一定过原点.( )
(3)如果函数f(x),g(x)为定义域相同的偶函数,则F(x)=f(x)+g(x)是偶函数.( )
(4)定义域关于原点对称是函数具有奇偶性的一个必要条件.( )
(5)若T是函数的一个周期,则nT(n∈Z,n≠0)也是函数的周期.( )
√
×
√
√
√
2.下列函数中为偶函数的是( )
A.y=x2sin x
B.y=x2cos x
C.y=|ln x|
D.y=2-x
奇函数
偶函数
定义域为(0,+∞),不具有奇偶性
既不是奇函数,也不是偶函数
B
偶函数须满足f(-x)=f(x)且定义域关于原点对称.
3.(易错题)已知函数f(x)=ax2+bx+3是定义在[a-3,2a]上的偶函数,则a+b的值是( )
A.-1 B.1
C.-3 D.0
因为函数f(x)=ax2+bx+3是定义在[a-3,2a]上的偶函数,
所以a-3+2a=0,
解得a=1.
由f(x)=f(-x)得b=0,
所以a+b=1.
B
4.已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x(1+x),则f(-1)=________.
f(-1)=-f(1)=-2
当x>0时, f(x)=x(1+x)
f(1)=1×2=2
f(x)为奇函数
-2
5.设f(x)是定义在R上的周期为2的函数,当x∈[-1,1)时,f(x)= 则f =________.
f = f
= f
=
=
1
考点梳理
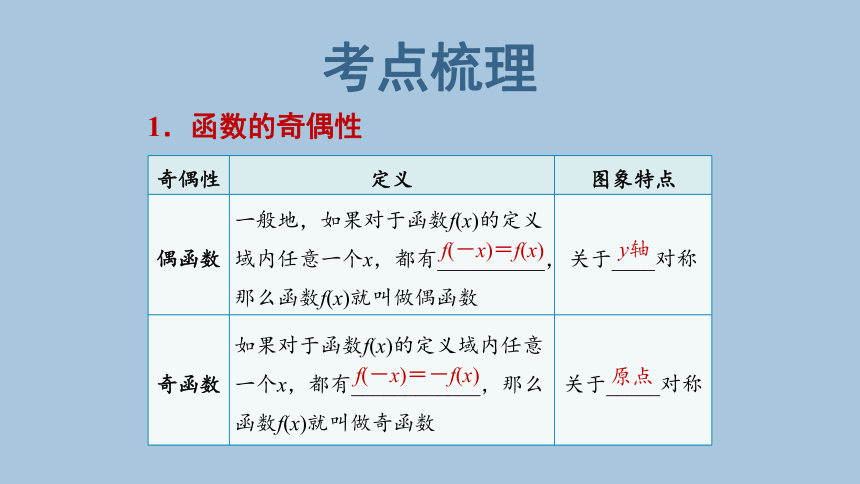
1.函数的奇偶性
奇偶性 定义 图象特点
偶函数 一般地,如果对于函数f(x)的定义域内任意一个x,都有__________,那么函数f(x)就叫做偶函数 关于____对称
奇函数 如果对于函数f(x)的定义域内任意一个x,都有____________,那么函数f(x)就叫做奇函数 关于_____对称
f(-x)=f(x)
y轴
f(-x)=-f(x)
原点
2.函数的周期性
(1)周期函数:对于函数y=f(x),如果存在一个非零常数T,使得当x取定义域内的任何值时,都有____________,那么就称函数y=f(x)为周期函数,称T为这个函数的周期.
(2)最小正周期:如果在周期函数f(x)的所有周期中存在一个_____的正数,那么这个______正数就叫做f(x)的最小正周期.
f(x+T)=f(x)
最小
最小
常用结论
(2)奇函数在两个对称的区间上具有相同的单调性,偶函数在两个对称的区间上具有相反的单调性.
(3)在公共定义域内有:奇±奇=奇,偶±偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇.
(1)如果函数f(x)是偶函数,那么f(x)=f(|x|).
函数奇偶性的常用结论
对f(x)定义域内任一自变量的值x:
(3)若f(x+a)=- ,则T=2a(a>0).
(2)若f(x+a)= ,则T=2a(a>0).
(1)若f(x+a)=-f(x),则T=2a(a>0).
函数周期性的常用结论
常用结论
常见误区
1.判断函数的奇偶性不可忽视函数的定义域.函数的定义域关于原点对称是函数具有奇偶性的必要不充分条件.
3.不是所有的周期函数都有最小正周期,如f(x)=5.
2.函数f(x)是奇函数,必须满足对定义域内的每一个x,都有f(-x)=-f(x),而不能说存在x0,使f(-x0)=-f(x0).同样偶函数也是如此.
典例剖析
考点
1
函数的奇偶性
角度一 判断函数的奇偶性
[例1] 判断下列函数的奇偶性.
(1)f(x)=x3+x,x∈[-1,4];
(2)f(x)=ln ;
(3)f(x)=;
(4)f(x)=
[例1] 判断下列函数的奇偶性.
(1)f(x)=x3+x,x∈[-1,4];
定义域不关于原点对称,所以f(x)既不是奇函数也不是偶函数.
(2)f(x)=ln ;
f(x)的定义域为(-2,2),
f(-x)=ln =-ln =-f(x),
所以函数f(x)为奇函数.
[例1] 判断下列函数的奇偶性.
(3)f(x)=;
f(x)的定义域为{-1,1},关于原点对称.
又f(-1)=f(1)=0,f(-1)=-f(1)=0,
所以f(x)既是奇函数又是偶函数.
[例1] 判断下列函数的奇偶性.
(4)f(x)=
f(x)的定义域为R,关于原点对称,
当x>0时,f(-x)=-(-x)2-2=-(x2+2)=-f(x);
当x<0时,f(-x)=(-x)2+2=-(-x2-2)=-f(x);
当x=0时,f(0)=0,也满足f(-x)=-f(x).
故该函数为奇函数.
方法总结
(2)判断f(x)与f(-x)的关系.在判断奇偶性时,可以转化为判断奇偶性的等价关系式f(x)+f(-x)=0(奇函数)或f(x)-f(-x)=0(偶函数)是否成立.
(1)定义域关于原点对称,这是函数具有奇偶性的必要不充分条件,所以首先考虑定义域.
常见特殊结构的奇偶函数:f(x)=loga(-x)(a>0且a≠1)为奇函数,f(x)=ax+a-x(a>0且a≠1)为偶函数.
函数具有奇偶性包括两个必备条件:
角度二 函数奇偶性的应用
[例2] (1)(2019·高考全国卷Ⅱ)设f(x)为奇函数,且当x≥0时,f(x)=ex-1,则当x<0时,f(x)=( )
A.e-x-1 B.e-x+1
C.-e-x-1 D.-e-x+1
通解
D
f(x)为奇函数
f(x)=-f(-x)
当x≥0时,f(x)=ex-1
当x<0时,f(x)=-f(-x)=-(e-x-1)=-e-x+1
角度二 函数奇偶性的应用
[例2] (1)(2019·高考全国卷Ⅱ)设f(x)为奇函数,且当x≥0时,f(x)=ex-1,则当x<0时,f(x)=( )
A.e-x-1 B.e-x+1
C.-e-x-1 D.-e-x+1
D
优解
依题意得,f(-1)=-f(1)=-(e1-1)=1-e,
结合选项知,选D.
角度二 函数奇偶性的应用
设g(x)=f(x)+1=-sin 2x+ ,易知g(x)是奇函数,
则g(a)=f(a)+1=- +1= ,
所以g(-a)=-g(a)=- ,
即f(-a)+1=- ,所以f(-a)=- .
[例2] (2) (2021·黑龙江哈尔滨师范大学附中月考)已知函数f(x)=cos+ -1,若f(a)=-,则f(-a)=( )
A. B. C.- D.-
D
方法总结
(3)求解析式中的参数:利用待定系数法求解,根据f(x)±f(-x)=0得到关于参数的恒等式,由系数的对等性得参数的方程或方程(组),进而得出参数的值.
(1)求函数值:将待求值利用奇偶性转化为已知区间上的函数值求解.
(2)求解析式:将待求区间上的自变量转化到已知区间上,再利用奇偶性求出.
已知函数奇偶性可以解决的3个问题
跟踪训练
1.函数f(x)= 为奇函数,则实数a=( )
A.-1 B.1 C.- D.
此时f(x)= 为奇函数
f(x)为奇函数
f(0)=0
0+2a+3=0
a=-
C
2.如果f(x)是定义在R上的奇函数,那么下列函数中,一定为偶函数的是( )
A.y=x+f(x) B.y=xf(x)
C.y=x2+f(x) D.y=x2f(x)
f(-x)=-f(x)
g(-x)=-x+f(-x)=-x-f(x)=-g(x)
奇函数
g(-x)=-xf(-x)=xf(x)=g(x)
偶函数
g(-x)=(-x)2+f(-x)=x2-f(x)
非奇非偶函数
g(-x)=(-x)2f(-x)=-x2f(x)=-g(x)
奇函数
B
因为函数f(x),g(x)分别是定义在R上的偶函数、奇函数,且满足f(x)+2g(x)=ex ①,
所以f(-x)+2g(-x)=e-x,即f(x)-2g(x)=e-x②.
联立①②
f(x)+2g(x)=ex
f(x)-2g(x)=e-x
解得
f(x)=
g(x)=
所以f(-2)= ,f(-3)= ,g(-1)= <0,
所以g(-1)3.(多选)若函数f(x),g(x)分别是定义在R上的偶函数、奇函数,且满足f(x)+2g(x)=ex,则( )
A.f(x)= B.g(x)=
C.f(-2)AD
当x<0时,-x>0,所以f(-x)=x2+x.
又因为函数f(x)为奇函数,
所以f(x)=-f(-x)=-x2-x=- + ,
所以当x<0时,函数f(x)的最大值为.
法一
4.(一题多解)已知函数f(x)为奇函数,当x>0时,f(x)=x2-x,则当x<0时,函数f(x)的最大值为________.
4.(一题多解)已知函数f(x)为奇函数,当x>0时,f(x)=x2-x,则当x<0时,函数f(x)的最大值为________.
法二
当x>0时,f(x)=x2-x= - ,最小值为-,
因为函数f(x)为奇函数,
所以当x<0时,函数f(x)的最大值为.
考点
2
函数的周期性
[例3] (1) (2020·广东六校第一次联考)在R上函数f(x)满足f(x+1)=f(x-1),且f(x)= ,其中a∈R,若f(-5)=f(4.5),则a=( )
A.0.5 B.1.5 C.2.5 D.3.5
C
f(x+1)=f(x-1)
f(x)是周期为2的函数
f(-5)=f(4.5)
f(-1)=f(0.5)
-1+a=1.5
a=2.5
[例3] (2)已知f(x)是R上最小正周期为2的周期函数,且当0≤x<2时,f(x)=x3-x,则函数y=f(x)的图象在区间[0,4]上与x轴的交点的个数为( )
A.2 B.3 C.4 D.5
考点
2
函数的周期性
当2≤x<4时,0≤x-2<2,又f(x)的最小正周期为2,
所以f(x-2)=f(x),所以f(x)=(x-2)(x-1)(x-3),
所以当2≤x<4时,y=f(x)的图象与x轴交点的横坐标分别为x3=2,x4=3.
当0≤x<2时,令f(x)=x3-x=x(x2-1)=0,
所以y=f(x)的图象与x轴交点的横坐标分别为x1=0,x2=1.
综上可知,共有5个交点.
又f(4)=f(2)=f(0)=0,
D
方法总结
(2)根据函数的周期性,可以由函数局部的性质得到函数的整体性质,在解决具体问题时,要注意结论:若T是函数的周期,则kT(k∈Z且k≠0)也是函数的周期.
(1)判断函数的周期性只需证明f(x+T)=f(x)(T≠0)便可证明函数是周期函数,且周期为T,函数的周期性常与函数的其他性质综合命题.
函数周期性的判定与应用
跟踪训练
因为f(x+2)=- ,
所以f(x+4)=- =f(x),
所以函数y=f(x)的周期T=4.
f(17)=f(4×4+1)=f(1)=1.
1.已知定义在R上的函数满足f(x+2)=-,当x∈(0,2]时,f(x)=2x-1.则f(17)=________.
1
跟踪训练
因为f(x+4)=f(x-2),
所以f(x+6)=f(x),则T=6是f(x)的周期.
所以f(2023)=f(337×6+1)=f(1).
又f(x)在R上是偶函数,
所以f(1)=f(-1)=6-(-1)=6,即f(2023)=6.
2.已知f(x)是定义在R上的偶函数,且f(x+4)=f(x-2).若当x∈[-3,0]时,f(x)=6-x,则f(2023)=________.
6
随堂训练
因为f(x+3)=f(x),
所以f(x)是定义在R上的以3为周期的周期函数,
所以f(7)=f(7-9)=f(-2).
又因为函数f(x)是偶函数,
所以f(-2)=f(2),所以f(7)=f(2)>1,
所以a>1,即a∈(1,+∞).
1.定义在R上的偶函数f(x)满足f(x+3)=f(x).若f(2)>1,f(7)=a,则实数a的取值范围为( )
A.(-∞,-3) B.(3,+∞) C.(-∞,-1) D.(1,+∞)
D
因为f(x)是定义在R上的偶函数,
所以当x<0时,-x>0.
由已知f(-x)=(-x)2-(-x)-1=x2+x-1=f(x),
所以f(x)=x2+x-1.
2.已知f(x)是R上的偶函数,且当x>0时,f(x)=x2-x-1,则当x<0时,f(x)=___________.
x2+x-1
3.若函数f(x)= 为奇函数,则实数a的值为________,且当x≥4时,f(x)的最大值为________.
所以当x=4时,f(x)max= .
由f(x)为奇函数易知a=2,
当x≥4时,f(x)= 在[4,+∞)上单调递减,
2
4.已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x).若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=________.
因为f(x)在R上是奇函数,且f(1-x)=f(1+x).
所以f(x+1)=-f(x-1),即f(x+2)=-f(x).
因此f(x+4)=f(x),则函数f(x)是周期为4的函数,
法一
由于f(1-x)=f(1+x),f(1)=2,
故令x=1,得f(0)=f(2)=0,
令x=2,得f(3)=f(-1)=-f(1)=-2,
令x=3,得f(4)=f(-2)=-f(2)=0,
故f(1)+f(2)+f(3)+f(4)=2+0-2+0=0,
所以f(1)+f(2)+f(3)+…+f(50)=12×0+f(1)+f(2)=2.
2
4.已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x).若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=________.
2
法二
取一个符合题意的函数f(x)=2sin ,
则结合该函数的图象易知数列{f(n)}(n∈N*)是以4为周期的周期数列.
故f(1)+f(2)+f(3)+…+f(50)
=12×[f(1)+f(2)+f(3)+f(4)]+f(1)+f(2)
=12×[2+0+(-2)+0]+2+0
=2.
5.设函数f(x)是定义在R上的奇函数,对任意实数x有f =-f 成立.
(1)证明y=f(x)是周期函数,并指出其周期;
因为f =-f ,且f(-x)=-f(x),
所以f(x+3)=f
=-f
=-f(-x)=f(x),
所以y=f(x)是周期函数,且3是其一个周期.
5.设函数f(x)是定义在R上的奇函数,对任意实数x有f =-f 成立.
(2)若f(1)=2,求f(2)+f(3)的值.
因为f(x)为定义在R上的奇函数,
所以f(0)=0,
且f(-1)=-f(1)=-2,
又T=3是y=f(x)的一个周期,
所以f(2)+f(3)=f(-1)+f(0)=-2+0=-2.
本课小结
本节知识以理解函数的奇偶性、会用函数的奇偶性为主,常与函数的单调性、周期性与对称性交汇命题,加强函数与方程思想、转化与化归思想的应用意识,题型以选择、填空题为主,中等偏上难度.
函数的奇偶性及周期性
考纲分析
课程标准解读 关联考点 核心素养
1.结合具体函数,了解函数奇偶性的含义. 2.会运用函数图象理解和研究函数的奇偶性. 3.了解函数周期性、最小正周期的含义,会判断、应用简单函数的周期性. 1.函数的奇偶性. 2.函数的周期性. 3.函数性质的综合应用. 1.数学抽象.
2.逻辑推理.
3.数学运算.
课前自测
1.判断正误(正确的打“√”,错误的打“×”)
(1)若f(x)是定义在R上的奇函数,则f(-x)+f(x)=0.( )
(2)偶函数的图象不一定过原点,奇函数的图象一定过原点.( )
(3)如果函数f(x),g(x)为定义域相同的偶函数,则F(x)=f(x)+g(x)是偶函数.( )
(4)定义域关于原点对称是函数具有奇偶性的一个必要条件.( )
(5)若T是函数的一个周期,则nT(n∈Z,n≠0)也是函数的周期.( )
√
×
√
√
√
2.下列函数中为偶函数的是( )
A.y=x2sin x
B.y=x2cos x
C.y=|ln x|
D.y=2-x
奇函数
偶函数
定义域为(0,+∞),不具有奇偶性
既不是奇函数,也不是偶函数
B
偶函数须满足f(-x)=f(x)且定义域关于原点对称.
3.(易错题)已知函数f(x)=ax2+bx+3是定义在[a-3,2a]上的偶函数,则a+b的值是( )
A.-1 B.1
C.-3 D.0
因为函数f(x)=ax2+bx+3是定义在[a-3,2a]上的偶函数,
所以a-3+2a=0,
解得a=1.
由f(x)=f(-x)得b=0,
所以a+b=1.
B
4.已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x(1+x),则f(-1)=________.
f(-1)=-f(1)=-2
当x>0时, f(x)=x(1+x)
f(1)=1×2=2
f(x)为奇函数
-2
5.设f(x)是定义在R上的周期为2的函数,当x∈[-1,1)时,f(x)= 则f =________.
f = f
= f
=
=
1
考点梳理
1.函数的奇偶性
奇偶性 定义 图象特点
偶函数 一般地,如果对于函数f(x)的定义域内任意一个x,都有__________,那么函数f(x)就叫做偶函数 关于____对称
奇函数 如果对于函数f(x)的定义域内任意一个x,都有____________,那么函数f(x)就叫做奇函数 关于_____对称
f(-x)=f(x)
y轴
f(-x)=-f(x)
原点
2.函数的周期性
(1)周期函数:对于函数y=f(x),如果存在一个非零常数T,使得当x取定义域内的任何值时,都有____________,那么就称函数y=f(x)为周期函数,称T为这个函数的周期.
(2)最小正周期:如果在周期函数f(x)的所有周期中存在一个_____的正数,那么这个______正数就叫做f(x)的最小正周期.
f(x+T)=f(x)
最小
最小
常用结论
(2)奇函数在两个对称的区间上具有相同的单调性,偶函数在两个对称的区间上具有相反的单调性.
(3)在公共定义域内有:奇±奇=奇,偶±偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇.
(1)如果函数f(x)是偶函数,那么f(x)=f(|x|).
函数奇偶性的常用结论
对f(x)定义域内任一自变量的值x:
(3)若f(x+a)=- ,则T=2a(a>0).
(2)若f(x+a)= ,则T=2a(a>0).
(1)若f(x+a)=-f(x),则T=2a(a>0).
函数周期性的常用结论
常用结论
常见误区
1.判断函数的奇偶性不可忽视函数的定义域.函数的定义域关于原点对称是函数具有奇偶性的必要不充分条件.
3.不是所有的周期函数都有最小正周期,如f(x)=5.
2.函数f(x)是奇函数,必须满足对定义域内的每一个x,都有f(-x)=-f(x),而不能说存在x0,使f(-x0)=-f(x0).同样偶函数也是如此.
典例剖析
考点
1
函数的奇偶性
角度一 判断函数的奇偶性
[例1] 判断下列函数的奇偶性.
(1)f(x)=x3+x,x∈[-1,4];
(2)f(x)=ln ;
(3)f(x)=;
(4)f(x)=
[例1] 判断下列函数的奇偶性.
(1)f(x)=x3+x,x∈[-1,4];
定义域不关于原点对称,所以f(x)既不是奇函数也不是偶函数.
(2)f(x)=ln ;
f(x)的定义域为(-2,2),
f(-x)=ln =-ln =-f(x),
所以函数f(x)为奇函数.
[例1] 判断下列函数的奇偶性.
(3)f(x)=;
f(x)的定义域为{-1,1},关于原点对称.
又f(-1)=f(1)=0,f(-1)=-f(1)=0,
所以f(x)既是奇函数又是偶函数.
[例1] 判断下列函数的奇偶性.
(4)f(x)=
f(x)的定义域为R,关于原点对称,
当x>0时,f(-x)=-(-x)2-2=-(x2+2)=-f(x);
当x<0时,f(-x)=(-x)2+2=-(-x2-2)=-f(x);
当x=0时,f(0)=0,也满足f(-x)=-f(x).
故该函数为奇函数.
方法总结
(2)判断f(x)与f(-x)的关系.在判断奇偶性时,可以转化为判断奇偶性的等价关系式f(x)+f(-x)=0(奇函数)或f(x)-f(-x)=0(偶函数)是否成立.
(1)定义域关于原点对称,这是函数具有奇偶性的必要不充分条件,所以首先考虑定义域.
常见特殊结构的奇偶函数:f(x)=loga(-x)(a>0且a≠1)为奇函数,f(x)=ax+a-x(a>0且a≠1)为偶函数.
函数具有奇偶性包括两个必备条件:
角度二 函数奇偶性的应用
[例2] (1)(2019·高考全国卷Ⅱ)设f(x)为奇函数,且当x≥0时,f(x)=ex-1,则当x<0时,f(x)=( )
A.e-x-1 B.e-x+1
C.-e-x-1 D.-e-x+1
通解
D
f(x)为奇函数
f(x)=-f(-x)
当x≥0时,f(x)=ex-1
当x<0时,f(x)=-f(-x)=-(e-x-1)=-e-x+1
角度二 函数奇偶性的应用
[例2] (1)(2019·高考全国卷Ⅱ)设f(x)为奇函数,且当x≥0时,f(x)=ex-1,则当x<0时,f(x)=( )
A.e-x-1 B.e-x+1
C.-e-x-1 D.-e-x+1
D
优解
依题意得,f(-1)=-f(1)=-(e1-1)=1-e,
结合选项知,选D.
角度二 函数奇偶性的应用
设g(x)=f(x)+1=-sin 2x+ ,易知g(x)是奇函数,
则g(a)=f(a)+1=- +1= ,
所以g(-a)=-g(a)=- ,
即f(-a)+1=- ,所以f(-a)=- .
[例2] (2) (2021·黑龙江哈尔滨师范大学附中月考)已知函数f(x)=cos+ -1,若f(a)=-,则f(-a)=( )
A. B. C.- D.-
D
方法总结
(3)求解析式中的参数:利用待定系数法求解,根据f(x)±f(-x)=0得到关于参数的恒等式,由系数的对等性得参数的方程或方程(组),进而得出参数的值.
(1)求函数值:将待求值利用奇偶性转化为已知区间上的函数值求解.
(2)求解析式:将待求区间上的自变量转化到已知区间上,再利用奇偶性求出.
已知函数奇偶性可以解决的3个问题
跟踪训练
1.函数f(x)= 为奇函数,则实数a=( )
A.-1 B.1 C.- D.
此时f(x)= 为奇函数
f(x)为奇函数
f(0)=0
0+2a+3=0
a=-
C
2.如果f(x)是定义在R上的奇函数,那么下列函数中,一定为偶函数的是( )
A.y=x+f(x) B.y=xf(x)
C.y=x2+f(x) D.y=x2f(x)
f(-x)=-f(x)
g(-x)=-x+f(-x)=-x-f(x)=-g(x)
奇函数
g(-x)=-xf(-x)=xf(x)=g(x)
偶函数
g(-x)=(-x)2+f(-x)=x2-f(x)
非奇非偶函数
g(-x)=(-x)2f(-x)=-x2f(x)=-g(x)
奇函数
B
因为函数f(x),g(x)分别是定义在R上的偶函数、奇函数,且满足f(x)+2g(x)=ex ①,
所以f(-x)+2g(-x)=e-x,即f(x)-2g(x)=e-x②.
联立①②
f(x)+2g(x)=ex
f(x)-2g(x)=e-x
解得
f(x)=
g(x)=
所以f(-2)= ,f(-3)= ,g(-1)= <0,
所以g(-1)
A.f(x)= B.g(x)=
C.f(-2)
当x<0时,-x>0,所以f(-x)=x2+x.
又因为函数f(x)为奇函数,
所以f(x)=-f(-x)=-x2-x=- + ,
所以当x<0时,函数f(x)的最大值为.
法一
4.(一题多解)已知函数f(x)为奇函数,当x>0时,f(x)=x2-x,则当x<0时,函数f(x)的最大值为________.
4.(一题多解)已知函数f(x)为奇函数,当x>0时,f(x)=x2-x,则当x<0时,函数f(x)的最大值为________.
法二
当x>0时,f(x)=x2-x= - ,最小值为-,
因为函数f(x)为奇函数,
所以当x<0时,函数f(x)的最大值为.
考点
2
函数的周期性
[例3] (1) (2020·广东六校第一次联考)在R上函数f(x)满足f(x+1)=f(x-1),且f(x)= ,其中a∈R,若f(-5)=f(4.5),则a=( )
A.0.5 B.1.5 C.2.5 D.3.5
C
f(x+1)=f(x-1)
f(x)是周期为2的函数
f(-5)=f(4.5)
f(-1)=f(0.5)
-1+a=1.5
a=2.5
[例3] (2)已知f(x)是R上最小正周期为2的周期函数,且当0≤x<2时,f(x)=x3-x,则函数y=f(x)的图象在区间[0,4]上与x轴的交点的个数为( )
A.2 B.3 C.4 D.5
考点
2
函数的周期性
当2≤x<4时,0≤x-2<2,又f(x)的最小正周期为2,
所以f(x-2)=f(x),所以f(x)=(x-2)(x-1)(x-3),
所以当2≤x<4时,y=f(x)的图象与x轴交点的横坐标分别为x3=2,x4=3.
当0≤x<2时,令f(x)=x3-x=x(x2-1)=0,
所以y=f(x)的图象与x轴交点的横坐标分别为x1=0,x2=1.
综上可知,共有5个交点.
又f(4)=f(2)=f(0)=0,
D
方法总结
(2)根据函数的周期性,可以由函数局部的性质得到函数的整体性质,在解决具体问题时,要注意结论:若T是函数的周期,则kT(k∈Z且k≠0)也是函数的周期.
(1)判断函数的周期性只需证明f(x+T)=f(x)(T≠0)便可证明函数是周期函数,且周期为T,函数的周期性常与函数的其他性质综合命题.
函数周期性的判定与应用
跟踪训练
因为f(x+2)=- ,
所以f(x+4)=- =f(x),
所以函数y=f(x)的周期T=4.
f(17)=f(4×4+1)=f(1)=1.
1.已知定义在R上的函数满足f(x+2)=-,当x∈(0,2]时,f(x)=2x-1.则f(17)=________.
1
跟踪训练
因为f(x+4)=f(x-2),
所以f(x+6)=f(x),则T=6是f(x)的周期.
所以f(2023)=f(337×6+1)=f(1).
又f(x)在R上是偶函数,
所以f(1)=f(-1)=6-(-1)=6,即f(2023)=6.
2.已知f(x)是定义在R上的偶函数,且f(x+4)=f(x-2).若当x∈[-3,0]时,f(x)=6-x,则f(2023)=________.
6
随堂训练
因为f(x+3)=f(x),
所以f(x)是定义在R上的以3为周期的周期函数,
所以f(7)=f(7-9)=f(-2).
又因为函数f(x)是偶函数,
所以f(-2)=f(2),所以f(7)=f(2)>1,
所以a>1,即a∈(1,+∞).
1.定义在R上的偶函数f(x)满足f(x+3)=f(x).若f(2)>1,f(7)=a,则实数a的取值范围为( )
A.(-∞,-3) B.(3,+∞) C.(-∞,-1) D.(1,+∞)
D
因为f(x)是定义在R上的偶函数,
所以当x<0时,-x>0.
由已知f(-x)=(-x)2-(-x)-1=x2+x-1=f(x),
所以f(x)=x2+x-1.
2.已知f(x)是R上的偶函数,且当x>0时,f(x)=x2-x-1,则当x<0时,f(x)=___________.
x2+x-1
3.若函数f(x)= 为奇函数,则实数a的值为________,且当x≥4时,f(x)的最大值为________.
所以当x=4时,f(x)max= .
由f(x)为奇函数易知a=2,
当x≥4时,f(x)= 在[4,+∞)上单调递减,
2
4.已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x).若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=________.
因为f(x)在R上是奇函数,且f(1-x)=f(1+x).
所以f(x+1)=-f(x-1),即f(x+2)=-f(x).
因此f(x+4)=f(x),则函数f(x)是周期为4的函数,
法一
由于f(1-x)=f(1+x),f(1)=2,
故令x=1,得f(0)=f(2)=0,
令x=2,得f(3)=f(-1)=-f(1)=-2,
令x=3,得f(4)=f(-2)=-f(2)=0,
故f(1)+f(2)+f(3)+f(4)=2+0-2+0=0,
所以f(1)+f(2)+f(3)+…+f(50)=12×0+f(1)+f(2)=2.
2
4.已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x).若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=________.
2
法二
取一个符合题意的函数f(x)=2sin ,
则结合该函数的图象易知数列{f(n)}(n∈N*)是以4为周期的周期数列.
故f(1)+f(2)+f(3)+…+f(50)
=12×[f(1)+f(2)+f(3)+f(4)]+f(1)+f(2)
=12×[2+0+(-2)+0]+2+0
=2.
5.设函数f(x)是定义在R上的奇函数,对任意实数x有f =-f 成立.
(1)证明y=f(x)是周期函数,并指出其周期;
因为f =-f ,且f(-x)=-f(x),
所以f(x+3)=f
=-f
=-f(-x)=f(x),
所以y=f(x)是周期函数,且3是其一个周期.
5.设函数f(x)是定义在R上的奇函数,对任意实数x有f =-f 成立.
(2)若f(1)=2,求f(2)+f(3)的值.
因为f(x)为定义在R上的奇函数,
所以f(0)=0,
且f(-1)=-f(1)=-2,
又T=3是y=f(x)的一个周期,
所以f(2)+f(3)=f(-1)+f(0)=-2+0=-2.
本课小结
本节知识以理解函数的奇偶性、会用函数的奇偶性为主,常与函数的单调性、周期性与对称性交汇命题,加强函数与方程思想、转化与化归思想的应用意识,题型以选择、填空题为主,中等偏上难度.
