人教B版(2019)数学必修第一册综合复习:一元二次不等式及其解法课件(共37张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册综合复习:一元二次不等式及其解法课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 992.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 22:20:14 | ||
图片预览










文档简介
(共37张PPT)
一元二次不等式及其解法
考纲分析
课程标准解读 关联考点 核心素养
1.经历从实际情境中抽象出一元二次不等式模型的过程. 2.通过函数图象了解一元二次不等式与相应函数、方程的联系. 3.会解一元二次不等式. 1.一元二次不等式的解法. 2.一元二次不等式恒成立问题. 1.直观想象
2.数学运算
3.数学抽象
课前自测
1.判断正误(正确的打“√”,错误的打“×”)
(1)若不等式ax2+bx+c<0(a≠0)的解集为(x1,x2),则必有a>0.( )
(2)若方程ax2+bx+c=0(a≠0)没有实数根,则不等式ax2+bx+c>0的解集为R.( )
(3)不等式ax2+bx+c≤0在R上恒成立的条件是a<0且Δ=b2-4ac≤0.( )
(4)若二次函数y=ax2+bx+c的图象开口向下,则不等式ax2+bx+c<0的解集一定不是空集.( )
√
×
×
√
2.设集合A={x|x2+x-6≤0},集合B为函数y= 的定义域,则A∩B等于( )
A.(1,2) B.[1,2]
C.[1,2) D.(1,2]
所以A∩B={x|1A={x|x2+x-6≤0}={x|-3≤x≤2},
由x-1>0得x>1,即B={x|x>1},
D
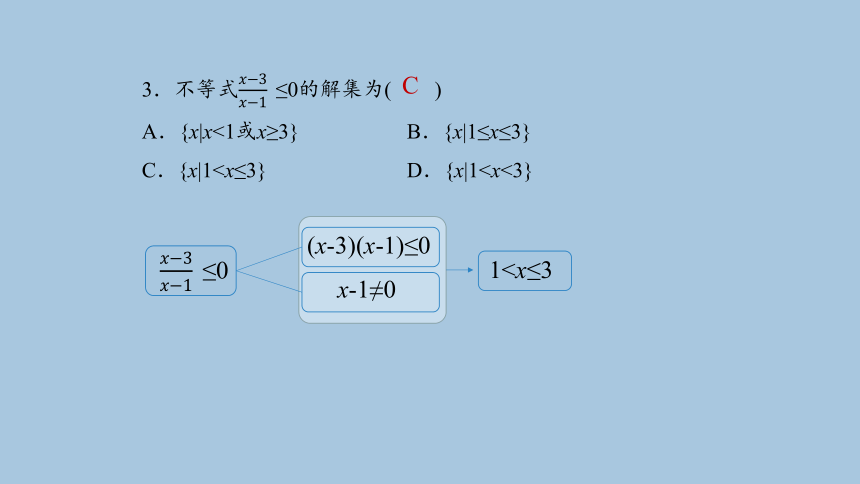
3.不等式≤0的解集为( )
A.{x|x<1或x≥3} B.{x|1≤x≤3}
C.{x|1≤0
(x-3)(x-1)≤0
x-1≠0
1C
-44.不等式-x2-3x+4>0的解集为________.
-x2-3x+4>0
(x+4)(x-1)<0
(-4,1)
5.(易错题)对于任意实数x,一元二次不等式mx2+mx-1<0恒成立,则实数m的取值范围是________.
所以m的取值范围是(-4,0).
m<0
=m2+4m<0
-4(-4,0)
考点梳理
1.一元一次不等式ax>b(a≠0)的解集
(1)当a>0时,解集为_____________.
(2)当a<0时,解集为_____________.
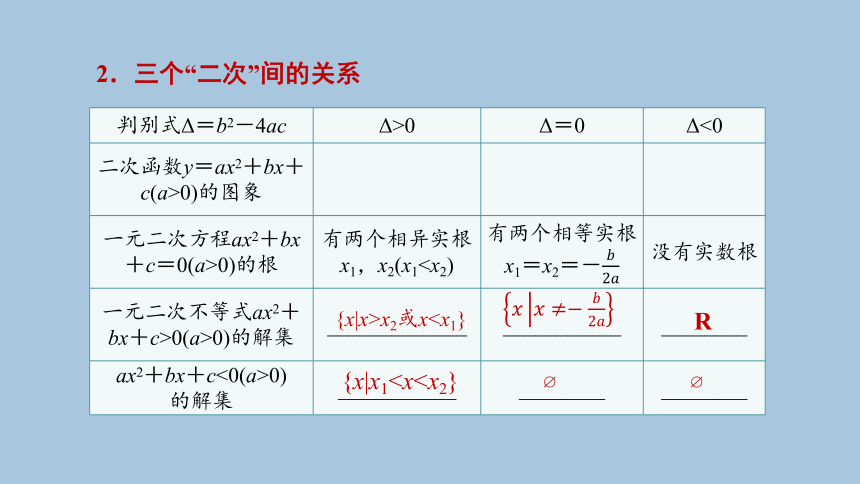
2.三个“二次”间的关系
判别式Δ=b2-4ac Δ>0 Δ=0 Δ<0
二次函数y=ax2+bx+c(a>0)的图象
一元二次方程ax2+bx+c=0(a>0)的根 有两个相异实根x1,x2(x1一元二次不等式ax2+bx+c>0(a>0)的解集 _____________ ___________ ________
ax2+bx+c<0(a>0) 的解集 ___________ ________ ________
{x|x>x2或xR
{x|x1
常用结论
分式不等式的解法
(1) >0(<0) f(x)g(x)>0(<0)
(2) ≥0(≤0)
两个恒成立的充要条件
(1)一元二次不等式ax2+bx+c>0对任意实数x恒成立
(2)一元二次不等式ax2+bx+c<0对任意实数x恒成立
常见误区
1.解不等式ax2+bx+c>0(<0)时不要忘记当a=0时的情形.
2.解不等式时忽视变形必须等价.
典例剖析
考点
1
一元二次不等式的解法
[例1] 解下列关于x的不等式.
(1) 0(2) ax2-(a+1)x+1<0(a>0).
[例1] 解下列关于x的不等式.
(1) 00x2-x-2>0
x2-x-2≤4
x2-x-2>0
x2-x-6≤0
(x+1)(x-2)>0
(x+2)(x-3)≤0
x >2或x<-1
-2≤ x≤ 3
借助于数轴,如图所示,
原不等式的解集为{x|-2≤x<-1或2[例1] 解下列关于x的不等式.
(2) ax2-(a+1)x+1<0(a>0).
因为a>0,原不等式等价于(x- )(x-1)<0.
①当a=1时, =1, (x- )(x-1)<0无解;
②当a>1时, <1,解(x- )(x-1)<0得③当01,解(x- )(x-1)<0得1综上所述,当0当a=1时,解集为 ;
当a>1时,解集为{x|方法总结
解一元二次不等式的方法和步骤
③确定方程无实根或有两个相同实根时,可直接写出解集;
确定方程有两个相异实根时,要讨论两实根的大小关系,从而确定解集.
①二次项若含有参数应讨论参数是等于0,小于0,还是大于0,然后将不等式转化为一次不等式或二次项系数为正的一元二次不等式;
②判断一元二次不等式所对应的方程实根的个数,即讨论判别式Δ与0的关系;
解含参数的一元二次不等式的步骤
方法总结
跟踪训练
1.不等式2x(x-7)>3(x-7)的解集为______________.
所以原不等式的解集为{x|x<或x>7}.
2x(x-7)>3(x-7)
2x(x-7)-3(x-7)>0
(x-7)(2x-3)>0
x<或x>7
{x|x<或x>7}
2.不等式+2≥0的解集为_____________.
+2≥0
≥0
(2x-1)(x-1)≥0
x-1≠0
x ≤ 或x>1
{x|x ≤ 或x>1}
3.解关于x的不等式:12x2-ax>a2(a∈R).
因为12x2-ax>a2,
所以12x2-ax-a2>0,即(4x+a)(3x-a)>0.
令(4x+a)(3x-a)=0,解得x1=-,x2=.
①当a>0时,-< ,解集为{x|x < -或x> };
②当a=0时,x2>0,解集为{x|x∈R,且x≠0};
③当a<0时,-> ,解集为{x|x< 或x >-}.
综上所述,当a>0时,不等式的解集为{x|x<-或x> };
当a=0时,不等式的解集为{x|x∈R,且x≠0};
当a<0时,不等式的解集为{x|x< 或}.
考点
2
一元二次不等式的恒成立问题
角度一 形如f(x)≥0(f(x)≤0)(x∈R)确定参数的范围
所以实数a的取值范围是(-2,2].
当a-2=0,即a=2时,不等式为-4<0,对一切x∈R恒成立.
当a≠2时,则
即,
解得-2[例2]若不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,则实数a的取值范围是________.
(-2,2]
方法总结
一元二次不等式在R上恒成立的条件
不等式类型(a≠0) 恒成立条件
ax2+bx+c>0 a>0,Δ<0
ax2+bx+c≥0 a>0,Δ≤0
ax2+bx+c<0 a<0,Δ<0
ax2+bx+c≤0 a<0,Δ≤0
角度二 形如f(x)≥0(f(x)≤0)(x∈[a,b])确定参数的范围
[例3] 若不等式x2≥m+4x在[0,1]上恒成立,则实数m的取值范围是( )
A.m≤-3或m≥0 B.m≥-3
C.-3≤m≤0 D.m≤-3
因为不等式x2≥m+4x在[0,1]上恒成立,
所以只需m≤(x2-4x)min,x∈[0,1],
令f(x)=x2-4x=(x-2)2-4,x∈[0,1],
所以f(x)min=f(1)=-3,
所以m≤-3.
D
方法总结
(1)根据函数的单调性,求其最值,让最值大于等于或小于等于0,从而求出参数的范围.
(2)数形结合,利用二次函数在端点a,b处的取值特点确定不等式求参数的取值范围.
形如f(x)≥0(f(x)≤0)(x∈[a,b])恒成立问题的求解思路
角度三 给定参数范围的恒成立问题
[例4] 已知a∈[-1,1]时不等式x2+(a-4)x+4-2a>0恒成立,则x的取值范围为( )
A.(-∞,2)∪(3,+∞) B.(-∞,1)∪(2,+∞)
C.(-∞,1)∪(3,+∞) D.(1,3)
解不等式组得x<1或x>3.
把不等式的左端看成关于a的一次函数,记f(a)=(x-2)a+x2-4x+4,
则由f(a)>0对于任意的a∈[-1,1]恒成立,
得f(-1)=x2-5x+6>0,且f(1)=x2-3x+2>0即可,
C
方法总结
已知参数范围求函数自变量的范围的一般思路是更换主元法.把参数当作函数的自变量,得到一个新的函数,然后利用新函数求解.
跟踪训练
函数f(x)=x2+ax+3.
(1)若当x∈R时,f(x)≥a恒成立,求实数a的取值范围;
(2)若当x∈[-2,2]时,f(x)≥a恒成立,求实数a的取值范围;
(3)若当a∈[4,6]时,f(x)≥0恒成立,求实数x的取值范围.
函数f(x)=x2+ax+3.
(1)若当x∈R时,f(x)≥a恒成立,求实数a的取值范围;
所以实数a的取值范围是[-6,2].
当x∈R时,x2+ax+3-a≥0恒成立
Δ=a2-4(3-a)≤0
a2+4a-12≤0
-6≤a≤2
函数f(x)=x2+ax+3.
(2)若当x∈[-2,2]时,f(x)≥a恒成立,求实数a的取值范围;
当-<-2,即a>4时,g(x)min=g(-2)=7-3a≥0,解得a≤ ,舍去;
由题意可转化为x2+ax+3-a≥0在x∈[-2,2]上恒成立,
则(x2+ax+3-a)min≥0(x∈[-2,2]).
令g(x)=x2+ax+3-a,x∈[-2,2],
函数图象的对称轴方程为x=-.
当-2≤-≤2,即-4≤a≤4时,g(x)min=g(-)=--a+3≥0,
解得-6≤a≤2,所以-4≤a≤2;
当->2,即a<-4时,g(x)min=g(2)=7+a≥0,
解得a≥-7,
所以-7≤a<-4.
综上可得,满足条件的实数a的取值范围是[-7,2].
函数f(x)=x2+ax+3.
(3)若当a∈[4,6]时,f(x)≥0恒成立,求实数x的取值范围.
所以实数x的取值范围是
(-∞,-3-]∪[-3+,+∞).
令h(a)=xa+x2+3,
当a∈[4,6]时,h(a)≥0恒成立.
只需,即
解得x≤-3-或x≥-3+.
随堂训练
1.若关于x的不等式x2+2ax+1≥0在区间[0,+∞)上恒成立,则实数a的取值范围是________.
所以Δ=4a2-4≤0或,解得a≥-1.
法一
当x=0时,1≥0对任意的a∈R恒成立,
当x≠0时,因为不等式x2+2ax+1≥0在区间(0,+∞)上恒成立,
所以x2+2ax+1=0在R上无解或有两个相等的实根或x2+2ax+1=0有两个不等的实根且两根均小于0,
[-1,+∞)
随堂训练
1.若关于x的不等式x2+2ax+1≥0在区间[0,+∞)上恒成立,则实数a的取值范围是________.
法二
[-1,+∞)
因为x=0时,1≥0对任意的a∈R恒成立,
当x≠0时,不等式可化为-2a≤x+(x∈(0,+∞)),
由基本不等式得x+≥2,当且仅当x=时取等号,
所以易知-2a≤2,解得a≥-1.
综上,a≥-1.
2.若不等式ax2+5x-2>0的解集是.
(1)求实数a的值;
(2)求不等式ax2-5x+a2-1>0的解集.
(1)由题意知a<0,且方程ax2+5x-2=0的两个根为,2,代入方程解得a=-2.
(2)由(1)知不等式ax2-5x+a2-1>0,
即为-2x2-5x+3>0,即2x2+5x-3<0,解得-3即不等式ax2-5x+a2-1>0的解集为(-3, ) .
3.已知函数f(x)=ax2+bx+c(a>0,b,c∈R).
(1)若函数f(x)的最小值是f(-1)=0,且c=1,F(x)= 求F(2)+F(-2)的值;
因为f(x)的最小值是f(-1)=0,且c=1,
所以,得,
所以f(x)=x2+2x+1=(x+1)2,
因为F(x)= ,
所以F(2)+F(-2)=8.
3.已知函数f(x)=ax2+bx+c(a>0,b,c∈R).
(2)若a=1,c=0,且|f(x)|≤1在区间(0,1]上恒成立,试求b的取值范围.
由题知f(x)=x2+bx,原命题等价于-1≤x2+bx≤1在x∈(0,1]上恒成立,
即b≤-x且b≥--x在x∈(0,1]恒成立,
根据单调性可得-x的最小值为0,--x的最大值为-2,
所以-2≤b≤0.
4.(多选)若不等式ax2-bx+c>0的解集是(-1,2),则下列选项正确的是( )
A.b<0且c>0
B.a-b+c>0
C.a+b+c>0
D.不等式ax2+bx+c>0的解集是(-2,1)
对于D,因为对于方程ax2+bx+c=0,设其两根为x1,x2,所以x1+x2=-=-1,x1x2==-2,所以两根分别为-2和1.所以不等式ax2+bx+c>0的解集是(-2,1),所以D正确.
对于A,a<0,-1,2是方程ax2-bx+c=0的两个根,
所以-1+2=1=,-1×2=,所以b=a,c=-2a,所以b<0,c>0,所以A正确;
√
令f(x)=ax2-bx+c,对于B,由题意可知f(1)=a-b+c>0,所以B正确;
对于C,f(-1)=a+b+c=0,所以C错误;
√
×
√
ABD
5.若不等式x2-(a+1)x+a≤0的解集是[-4,3]的子集,则a的取值范围是( )
A.[-4,1] B.[-4,3]
C.[1,3] D.[-1,3]
原不等式为(x-a)(x-1)≤0,
当a<1时,不等式的解集为[a,1],此时只要a≥-4即可,即-4≤a<1;
当a=1时,不等式的解集为{x|x=1},此时符合要求;
当a>1时,不等式的解集为[1,a],此时只要a≤3即可,即1综上可得-4≤a≤3.
B
本课小结
一元二次不等式解法是不等式中的重要内容,“三个二次”之间的联系的综合应用等问题是高考的热点.
一元二次不等式及其解法
考纲分析
课程标准解读 关联考点 核心素养
1.经历从实际情境中抽象出一元二次不等式模型的过程. 2.通过函数图象了解一元二次不等式与相应函数、方程的联系. 3.会解一元二次不等式. 1.一元二次不等式的解法. 2.一元二次不等式恒成立问题. 1.直观想象
2.数学运算
3.数学抽象
课前自测
1.判断正误(正确的打“√”,错误的打“×”)
(1)若不等式ax2+bx+c<0(a≠0)的解集为(x1,x2),则必有a>0.( )
(2)若方程ax2+bx+c=0(a≠0)没有实数根,则不等式ax2+bx+c>0的解集为R.( )
(3)不等式ax2+bx+c≤0在R上恒成立的条件是a<0且Δ=b2-4ac≤0.( )
(4)若二次函数y=ax2+bx+c的图象开口向下,则不等式ax2+bx+c<0的解集一定不是空集.( )
√
×
×
√
2.设集合A={x|x2+x-6≤0},集合B为函数y= 的定义域,则A∩B等于( )
A.(1,2) B.[1,2]
C.[1,2) D.(1,2]
所以A∩B={x|1
由x-1>0得x>1,即B={x|x>1},
D
3.不等式≤0的解集为( )
A.{x|x<1或x≥3} B.{x|1≤x≤3}
C.{x|1
(x-3)(x-1)≤0
x-1≠0
1
-4
-x2-3x+4>0
(x+4)(x-1)<0
(-4,1)
5.(易错题)对于任意实数x,一元二次不等式mx2+mx-1<0恒成立,则实数m的取值范围是________.
所以m的取值范围是(-4,0).
m<0
=m2+4m<0
-4
考点梳理
1.一元一次不等式ax>b(a≠0)的解集
(1)当a>0时,解集为_____________.
(2)当a<0时,解集为_____________.
2.三个“二次”间的关系
判别式Δ=b2-4ac Δ>0 Δ=0 Δ<0
二次函数y=ax2+bx+c(a>0)的图象
一元二次方程ax2+bx+c=0(a>0)的根 有两个相异实根x1,x2(x1
ax2+bx+c<0(a>0) 的解集 ___________ ________ ________
{x|x>x2或x
{x|x1
常用结论
分式不等式的解法
(1) >0(<0) f(x)g(x)>0(<0)
(2) ≥0(≤0)
两个恒成立的充要条件
(1)一元二次不等式ax2+bx+c>0对任意实数x恒成立
(2)一元二次不等式ax2+bx+c<0对任意实数x恒成立
常见误区
1.解不等式ax2+bx+c>0(<0)时不要忘记当a=0时的情形.
2.解不等式时忽视变形必须等价.
典例剖析
考点
1
一元二次不等式的解法
[例1] 解下列关于x的不等式.
(1) 0
[例1] 解下列关于x的不等式.
(1) 0
x2-x-2≤4
x2-x-2>0
x2-x-6≤0
(x+1)(x-2)>0
(x+2)(x-3)≤0
x >2或x<-1
-2≤ x≤ 3
借助于数轴,如图所示,
原不等式的解集为{x|-2≤x<-1或2
(2) ax2-(a+1)x+1<0(a>0).
因为a>0,原不等式等价于(x- )(x-1)<0.
①当a=1时, =1, (x- )(x-1)<0无解;
②当a>1时, <1,解(x- )(x-1)<0得
当a>1时,解集为{x|
解一元二次不等式的方法和步骤
③确定方程无实根或有两个相同实根时,可直接写出解集;
确定方程有两个相异实根时,要讨论两实根的大小关系,从而确定解集.
①二次项若含有参数应讨论参数是等于0,小于0,还是大于0,然后将不等式转化为一次不等式或二次项系数为正的一元二次不等式;
②判断一元二次不等式所对应的方程实根的个数,即讨论判别式Δ与0的关系;
解含参数的一元二次不等式的步骤
方法总结
跟踪训练
1.不等式2x(x-7)>3(x-7)的解集为______________.
所以原不等式的解集为{x|x<或x>7}.
2x(x-7)>3(x-7)
2x(x-7)-3(x-7)>0
(x-7)(2x-3)>0
x<或x>7
{x|x<或x>7}
2.不等式+2≥0的解集为_____________.
+2≥0
≥0
(2x-1)(x-1)≥0
x-1≠0
x ≤ 或x>1
{x|x ≤ 或x>1}
3.解关于x的不等式:12x2-ax>a2(a∈R).
因为12x2-ax>a2,
所以12x2-ax-a2>0,即(4x+a)(3x-a)>0.
令(4x+a)(3x-a)=0,解得x1=-,x2=.
①当a>0时,-< ,解集为{x|x < -或x> };
②当a=0时,x2>0,解集为{x|x∈R,且x≠0};
③当a<0时,-> ,解集为{x|x< 或x >-}.
综上所述,当a>0时,不等式的解集为{x|x<-或x> };
当a=0时,不等式的解集为{x|x∈R,且x≠0};
当a<0时,不等式的解集为{x|x< 或}.
考点
2
一元二次不等式的恒成立问题
角度一 形如f(x)≥0(f(x)≤0)(x∈R)确定参数的范围
所以实数a的取值范围是(-2,2].
当a-2=0,即a=2时,不等式为-4<0,对一切x∈R恒成立.
当a≠2时,则
即,
解得-2
(-2,2]
方法总结
一元二次不等式在R上恒成立的条件
不等式类型(a≠0) 恒成立条件
ax2+bx+c>0 a>0,Δ<0
ax2+bx+c≥0 a>0,Δ≤0
ax2+bx+c<0 a<0,Δ<0
ax2+bx+c≤0 a<0,Δ≤0
角度二 形如f(x)≥0(f(x)≤0)(x∈[a,b])确定参数的范围
[例3] 若不等式x2≥m+4x在[0,1]上恒成立,则实数m的取值范围是( )
A.m≤-3或m≥0 B.m≥-3
C.-3≤m≤0 D.m≤-3
因为不等式x2≥m+4x在[0,1]上恒成立,
所以只需m≤(x2-4x)min,x∈[0,1],
令f(x)=x2-4x=(x-2)2-4,x∈[0,1],
所以f(x)min=f(1)=-3,
所以m≤-3.
D
方法总结
(1)根据函数的单调性,求其最值,让最值大于等于或小于等于0,从而求出参数的范围.
(2)数形结合,利用二次函数在端点a,b处的取值特点确定不等式求参数的取值范围.
形如f(x)≥0(f(x)≤0)(x∈[a,b])恒成立问题的求解思路
角度三 给定参数范围的恒成立问题
[例4] 已知a∈[-1,1]时不等式x2+(a-4)x+4-2a>0恒成立,则x的取值范围为( )
A.(-∞,2)∪(3,+∞) B.(-∞,1)∪(2,+∞)
C.(-∞,1)∪(3,+∞) D.(1,3)
解不等式组得x<1或x>3.
把不等式的左端看成关于a的一次函数,记f(a)=(x-2)a+x2-4x+4,
则由f(a)>0对于任意的a∈[-1,1]恒成立,
得f(-1)=x2-5x+6>0,且f(1)=x2-3x+2>0即可,
C
方法总结
已知参数范围求函数自变量的范围的一般思路是更换主元法.把参数当作函数的自变量,得到一个新的函数,然后利用新函数求解.
跟踪训练
函数f(x)=x2+ax+3.
(1)若当x∈R时,f(x)≥a恒成立,求实数a的取值范围;
(2)若当x∈[-2,2]时,f(x)≥a恒成立,求实数a的取值范围;
(3)若当a∈[4,6]时,f(x)≥0恒成立,求实数x的取值范围.
函数f(x)=x2+ax+3.
(1)若当x∈R时,f(x)≥a恒成立,求实数a的取值范围;
所以实数a的取值范围是[-6,2].
当x∈R时,x2+ax+3-a≥0恒成立
Δ=a2-4(3-a)≤0
a2+4a-12≤0
-6≤a≤2
函数f(x)=x2+ax+3.
(2)若当x∈[-2,2]时,f(x)≥a恒成立,求实数a的取值范围;
当-<-2,即a>4时,g(x)min=g(-2)=7-3a≥0,解得a≤ ,舍去;
由题意可转化为x2+ax+3-a≥0在x∈[-2,2]上恒成立,
则(x2+ax+3-a)min≥0(x∈[-2,2]).
令g(x)=x2+ax+3-a,x∈[-2,2],
函数图象的对称轴方程为x=-.
当-2≤-≤2,即-4≤a≤4时,g(x)min=g(-)=--a+3≥0,
解得-6≤a≤2,所以-4≤a≤2;
当->2,即a<-4时,g(x)min=g(2)=7+a≥0,
解得a≥-7,
所以-7≤a<-4.
综上可得,满足条件的实数a的取值范围是[-7,2].
函数f(x)=x2+ax+3.
(3)若当a∈[4,6]时,f(x)≥0恒成立,求实数x的取值范围.
所以实数x的取值范围是
(-∞,-3-]∪[-3+,+∞).
令h(a)=xa+x2+3,
当a∈[4,6]时,h(a)≥0恒成立.
只需,即
解得x≤-3-或x≥-3+.
随堂训练
1.若关于x的不等式x2+2ax+1≥0在区间[0,+∞)上恒成立,则实数a的取值范围是________.
所以Δ=4a2-4≤0或,解得a≥-1.
法一
当x=0时,1≥0对任意的a∈R恒成立,
当x≠0时,因为不等式x2+2ax+1≥0在区间(0,+∞)上恒成立,
所以x2+2ax+1=0在R上无解或有两个相等的实根或x2+2ax+1=0有两个不等的实根且两根均小于0,
[-1,+∞)
随堂训练
1.若关于x的不等式x2+2ax+1≥0在区间[0,+∞)上恒成立,则实数a的取值范围是________.
法二
[-1,+∞)
因为x=0时,1≥0对任意的a∈R恒成立,
当x≠0时,不等式可化为-2a≤x+(x∈(0,+∞)),
由基本不等式得x+≥2,当且仅当x=时取等号,
所以易知-2a≤2,解得a≥-1.
综上,a≥-1.
2.若不等式ax2+5x-2>0的解集是.
(1)求实数a的值;
(2)求不等式ax2-5x+a2-1>0的解集.
(1)由题意知a<0,且方程ax2+5x-2=0的两个根为,2,代入方程解得a=-2.
(2)由(1)知不等式ax2-5x+a2-1>0,
即为-2x2-5x+3>0,即2x2+5x-3<0,解得-3
3.已知函数f(x)=ax2+bx+c(a>0,b,c∈R).
(1)若函数f(x)的最小值是f(-1)=0,且c=1,F(x)= 求F(2)+F(-2)的值;
因为f(x)的最小值是f(-1)=0,且c=1,
所以,得,
所以f(x)=x2+2x+1=(x+1)2,
因为F(x)= ,
所以F(2)+F(-2)=8.
3.已知函数f(x)=ax2+bx+c(a>0,b,c∈R).
(2)若a=1,c=0,且|f(x)|≤1在区间(0,1]上恒成立,试求b的取值范围.
由题知f(x)=x2+bx,原命题等价于-1≤x2+bx≤1在x∈(0,1]上恒成立,
即b≤-x且b≥--x在x∈(0,1]恒成立,
根据单调性可得-x的最小值为0,--x的最大值为-2,
所以-2≤b≤0.
4.(多选)若不等式ax2-bx+c>0的解集是(-1,2),则下列选项正确的是( )
A.b<0且c>0
B.a-b+c>0
C.a+b+c>0
D.不等式ax2+bx+c>0的解集是(-2,1)
对于D,因为对于方程ax2+bx+c=0,设其两根为x1,x2,所以x1+x2=-=-1,x1x2==-2,所以两根分别为-2和1.所以不等式ax2+bx+c>0的解集是(-2,1),所以D正确.
对于A,a<0,-1,2是方程ax2-bx+c=0的两个根,
所以-1+2=1=,-1×2=,所以b=a,c=-2a,所以b<0,c>0,所以A正确;
√
令f(x)=ax2-bx+c,对于B,由题意可知f(1)=a-b+c>0,所以B正确;
对于C,f(-1)=a+b+c=0,所以C错误;
√
×
√
ABD
5.若不等式x2-(a+1)x+a≤0的解集是[-4,3]的子集,则a的取值范围是( )
A.[-4,1] B.[-4,3]
C.[1,3] D.[-1,3]
原不等式为(x-a)(x-1)≤0,
当a<1时,不等式的解集为[a,1],此时只要a≥-4即可,即-4≤a<1;
当a=1时,不等式的解集为{x|x=1},此时符合要求;
当a>1时,不等式的解集为[1,a],此时只要a≤3即可,即1
B
本课小结
一元二次不等式解法是不等式中的重要内容,“三个二次”之间的联系的综合应用等问题是高考的热点.
