人教A版(2019)高中数学选择性必修第一册1.1.1_空间向量及其运算_课件(共26张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册1.1.1_空间向量及其运算_课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 769.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 22:08:35 | ||
图片预览






文档简介
(共26张PPT)
第一章 1.1.1空间向量及其运算
1.经历向量及其运算由平面向空间推广的过程,了解空间向量、向量的模、零向量、相反向量、相等向量等的概念.
2.会用平行四边形法则、三角形法则作出向量的和与差,了解向量加法的交换律和结合律.
问题导学
题型探究
当堂训练
学习目标
知识点一 空间向量的概念
思考 类比平面向量的概念,给出空间向量的概念.
答案 在空间,把具有大小和方向的量叫做空间向量.
问题导学
方向
大小
长度
模
长度
(2)几类特殊的空间向量
名称 定义及表示
零向量 规定长度为0的向量叫_______,记为0
单位向量 ______的向量叫单位向量
相反向量 与向量a长度_____而方向_____的向量,称为a的相反向量,记为-a
相等向量 方向_____且模_____的向量称为相等向量,_____且_____的有向线段表示同一向量或相等向量
零向量
模为1
相等
相反
相同
相等
同向
等长
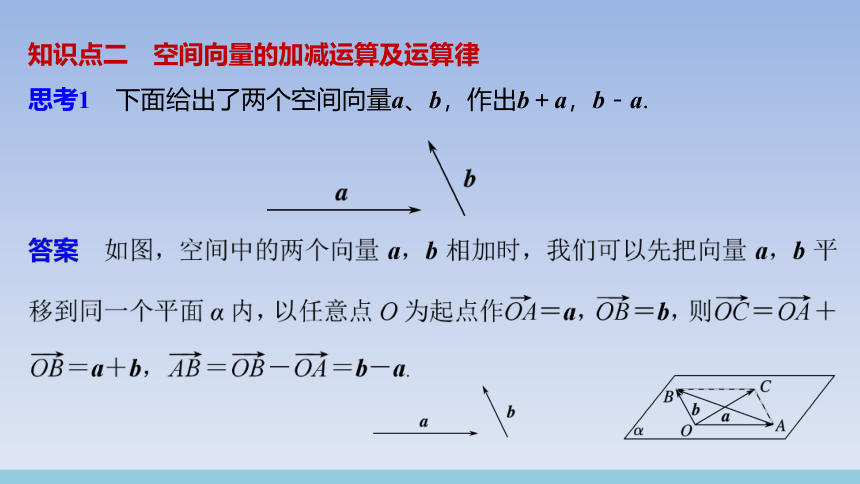
知识点二 空间向量的加减运算及运算律
思考1 下面给出了两个空间向量a、b,作出b+a,b-a.
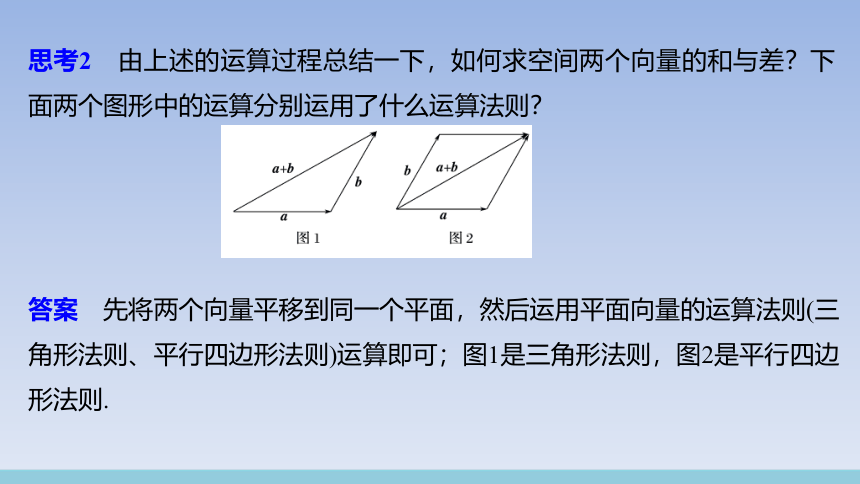
思考2 由上述的运算过程总结一下,如何求空间两个向量的和与差?下面两个图形中的运算分别运用了什么运算法则?
答案 先将两个向量平移到同一个平面,然后运用平面向量的运算法则(三角形法则、平行四边形法则)运算即可;图1是三角形法则,图2是平行四边形法则.
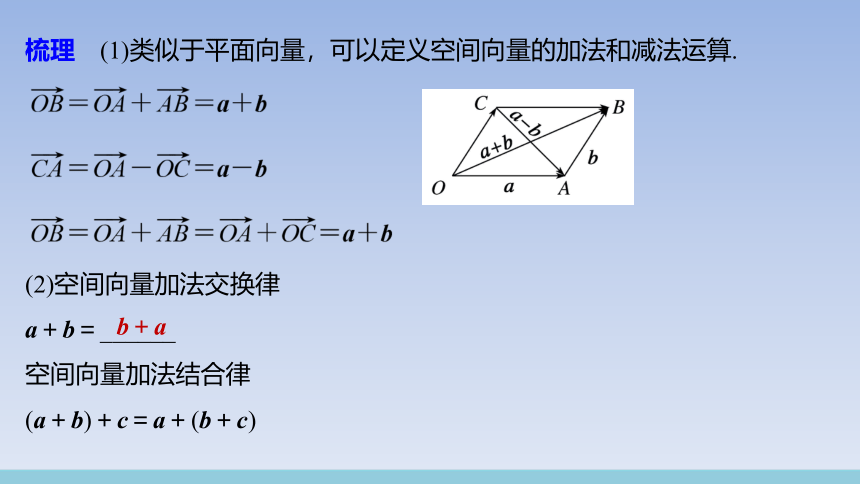
梳理 (1)类似于平面向量,可以定义空间向量的加法和减法运算.
(2)空间向量加法交换律
a+b=______
空间向量加法结合律
(a+b)+c=a+(b+c)
b+a
类型一 有关空间向量的概念的理解
题型探究
解析 两个空间向量相等,它们的起点、终点不一定相同,故①不正确;
若空间向量a,b满足|a|=|b|,则不一定能判断出a=b,故②不正确;
④显然正确;
空间中任意两个单位向量的模必相等,但这两个向量不一定相等,故⑤错误.故选C.
答案 C
在空间,平面向量、向量的模、相等向量的概念和平面向量完全一致,两向量相等的充要条件是两个向量的方向相同、模相等.两向量互为相反向量的充要条件是大小相等,方向相反.
反思与感悟
答案 B
解 ①假命题,有向线段是空间向量的一种表示形式,但不能把二者完全等同起来.
②假命题,不相等的两个空间向量的模也可以相等,只要它们的方向不相同即可.
③假命题,零向量的相反向量仍是零向量,但零向量与零向量是相等的.
类型二 空间向量的加减运算
例2 如图,已知长方体ABCD-A′B′C′D′,化简下列向量表达式,并在图中标出化简结果的向量.
根据向量相等的概念,向量运算时可以根据需要进行平移向量;化简向量表达式主要是利用平行四边形法则或三角形法则进行化简,在化简过程中遇到减法时可灵活应用相反向量转化成加法,也可以按减法法则进行运算,加减法之间可相互转化,另外化简的结果要在图中标注好.
反思与感悟
跟踪训练2 如图所示,已知平行六面体ABCDA1B1C1D1,M为A1C1与B1D1的交点,化简下列向量表达式.
1.下列命题中,假命题是( )
A.同平面向量一样,任意两个空间向量都不能比较大小
B.两个相等的向量,若起点相同,则终点也相同
C.只有零向量的模等于0
D.共线的单位向量都相等
D
当堂训练
解析 容易判断D是假命题,共线的单位向量是相等向量或相反向量.
1
2
3
4
5
1
2
3
4
5
C
1
2
3
4
5
解析 向量a,b互为相反向量,则a,b模相等、方向相反.故D正确.
D
3.向量a,b互为相反向量,已知|b|=3,则下列结论正确的是( )
A.a=b B.a+b为实数0
C.a与b方向相同 D.|a|=3
1
2
3
4
5
1
2
3
4
5
答案 4
1
2
3
4
5
0
规律与方法
(4)空间向量减法运算时,一定要抓住向量的起点与终点.
第一章 1.1.1空间向量及其运算
1.经历向量及其运算由平面向空间推广的过程,了解空间向量、向量的模、零向量、相反向量、相等向量等的概念.
2.会用平行四边形法则、三角形法则作出向量的和与差,了解向量加法的交换律和结合律.
问题导学
题型探究
当堂训练
学习目标
知识点一 空间向量的概念
思考 类比平面向量的概念,给出空间向量的概念.
答案 在空间,把具有大小和方向的量叫做空间向量.
问题导学
方向
大小
长度
模
长度
(2)几类特殊的空间向量
名称 定义及表示
零向量 规定长度为0的向量叫_______,记为0
单位向量 ______的向量叫单位向量
相反向量 与向量a长度_____而方向_____的向量,称为a的相反向量,记为-a
相等向量 方向_____且模_____的向量称为相等向量,_____且_____的有向线段表示同一向量或相等向量
零向量
模为1
相等
相反
相同
相等
同向
等长
知识点二 空间向量的加减运算及运算律
思考1 下面给出了两个空间向量a、b,作出b+a,b-a.
思考2 由上述的运算过程总结一下,如何求空间两个向量的和与差?下面两个图形中的运算分别运用了什么运算法则?
答案 先将两个向量平移到同一个平面,然后运用平面向量的运算法则(三角形法则、平行四边形法则)运算即可;图1是三角形法则,图2是平行四边形法则.
梳理 (1)类似于平面向量,可以定义空间向量的加法和减法运算.
(2)空间向量加法交换律
a+b=______
空间向量加法结合律
(a+b)+c=a+(b+c)
b+a
类型一 有关空间向量的概念的理解
题型探究
解析 两个空间向量相等,它们的起点、终点不一定相同,故①不正确;
若空间向量a,b满足|a|=|b|,则不一定能判断出a=b,故②不正确;
④显然正确;
空间中任意两个单位向量的模必相等,但这两个向量不一定相等,故⑤错误.故选C.
答案 C
在空间,平面向量、向量的模、相等向量的概念和平面向量完全一致,两向量相等的充要条件是两个向量的方向相同、模相等.两向量互为相反向量的充要条件是大小相等,方向相反.
反思与感悟
答案 B
解 ①假命题,有向线段是空间向量的一种表示形式,但不能把二者完全等同起来.
②假命题,不相等的两个空间向量的模也可以相等,只要它们的方向不相同即可.
③假命题,零向量的相反向量仍是零向量,但零向量与零向量是相等的.
类型二 空间向量的加减运算
例2 如图,已知长方体ABCD-A′B′C′D′,化简下列向量表达式,并在图中标出化简结果的向量.
根据向量相等的概念,向量运算时可以根据需要进行平移向量;化简向量表达式主要是利用平行四边形法则或三角形法则进行化简,在化简过程中遇到减法时可灵活应用相反向量转化成加法,也可以按减法法则进行运算,加减法之间可相互转化,另外化简的结果要在图中标注好.
反思与感悟
跟踪训练2 如图所示,已知平行六面体ABCDA1B1C1D1,M为A1C1与B1D1的交点,化简下列向量表达式.
1.下列命题中,假命题是( )
A.同平面向量一样,任意两个空间向量都不能比较大小
B.两个相等的向量,若起点相同,则终点也相同
C.只有零向量的模等于0
D.共线的单位向量都相等
D
当堂训练
解析 容易判断D是假命题,共线的单位向量是相等向量或相反向量.
1
2
3
4
5
1
2
3
4
5
C
1
2
3
4
5
解析 向量a,b互为相反向量,则a,b模相等、方向相反.故D正确.
D
3.向量a,b互为相反向量,已知|b|=3,则下列结论正确的是( )
A.a=b B.a+b为实数0
C.a与b方向相同 D.|a|=3
1
2
3
4
5
1
2
3
4
5
答案 4
1
2
3
4
5
0
规律与方法
(4)空间向量减法运算时,一定要抓住向量的起点与终点.
