人教A版(2019)高中数学选择性必修第一册《空间向量及其运算》知识探究课件(共21张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册《空间向量及其运算》知识探究课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
人教A版同步教材名师课件
空间向量及其运算
---知识探究
1.空位向量:在空间,具有大小和方向的量叫做空间向量.
2.长度或模:空间向量的大小.
3.表示方法
(1)几何表示法:空间向量用有向线段表示.
(2)字母表示法:用字母表示;若向量的起点是,终点是,也可记作:,其模记为或.
(3)坐标表示法:建立空间坐标系后,还可以用坐标表示空间向量.
4.常见的特殊向量
(1)零向量:长度为0的向量叫做零向量,记为0.
(2)单位向量:模为1的向量叫做单位向量.
探究点1 空间向量的相关概念
(3)相反向量:与向量长度相等而方向相反的向量,叫做的相反向量,记为.
(4)共线向量:如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量.
(5)方向向量:在直线上取非零向量,与向量平行的非零向量称为直线的方向向量.
(6)相等向量:方向相同且模相等的向量叫做相等向量.
探究点1 空间向量的相关概念
1.空间向量要紧紧抓住向量的两个要素,即大小和方向.
2.注意一些特殊向量的特性
(1)零向量不是没有方向,而是它的方向是任意的,且与任何向量都共线,这一点说明了共线向量不具备传递性.
(2)单位向量方向虽然不一定相同,但它们的长度都是1.
(3)两个向量模相等,不一定是相等向量;反之,若两个向量相等,则它们不仅模相等,方向也相同.若两个向量模相等,方向相反,则它们为相反向量.
要点辨析
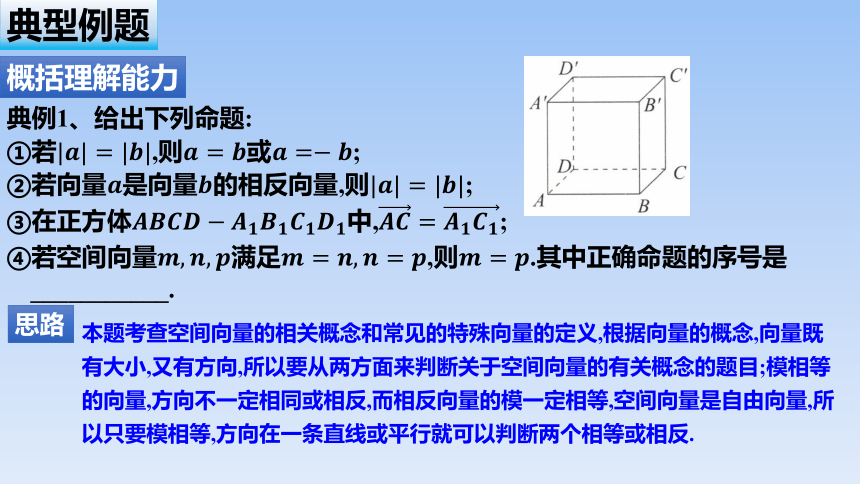
典例1、给出下列命题:
①若,则或;
②若向量是向量的相反向量,则;
③在正方体中,;
④若空间向量满足,则.其中正确命题的序号是___________.
思路
本题考查空间向量的相关概念和常见的特殊向量的定义,根据向量的概念,向量既有大小,又有方向,所以要从两方面来判断关于空间向量的有关概念的题目;模相等的向量,方向不一定相同或相反,而相反向量的模一定相等,空间向量是自由向量,所以只要模相等,方向在一条直线或平行就可以判断两个相等或相反.
概括理解能力
典型例题
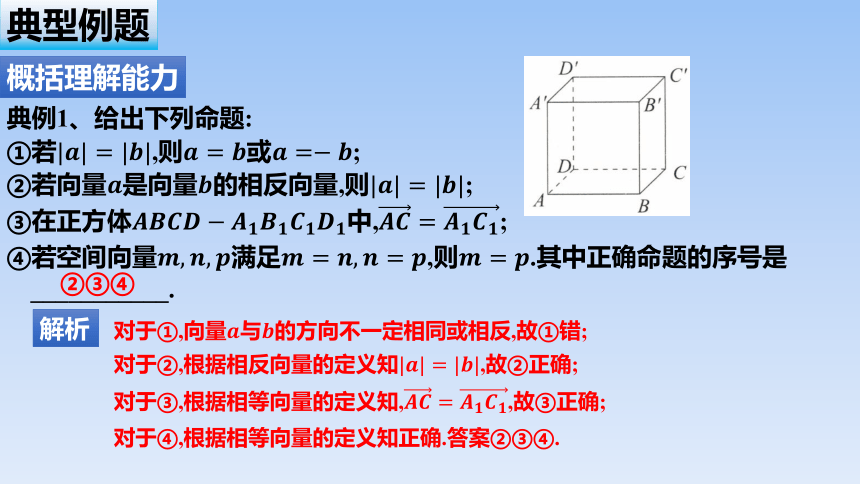
典例1、给出下列命题:
①若,则或;
②若向量是向量的相反向量,则;
③在正方体中,;
④若空间向量满足,则.其中正确命题的序号是___________.
概括理解能力
典型例题
解析
对于①,向量与的方向不一定相同或相反,故①错;
对于②,根据相反向量的定义知,故②正确;
对于③,根据相等向量的定义知,,故③正确;
对于④,根据相等向量的定义知正确.答案②③④.
②③④
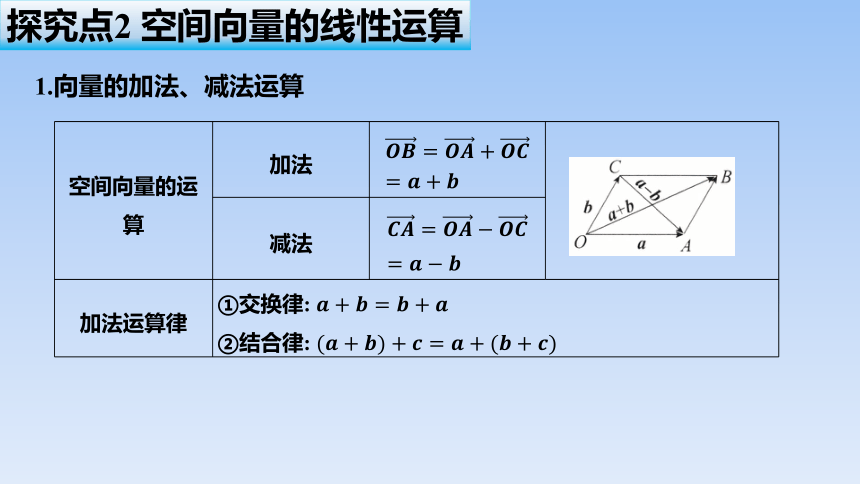
1.向量的加法、减法运算
探究点2 空间向量的线性运算
空间向量的运算 加法
减法
加法运算律 ①交换律: ②结合律:
探究点2 空间向量的线性运算
2.空间向量的数乘运算
(1)定义:实数与空间向量的乘积仍然是一个向量,称为向量的数乘运算.
当时,与向量方向相同;当时,与向量方向相反; 的长度是的长度的倍.
(2)运算律
①结合律:.
②分配律:.
1.空间向量加法、减法运算的两个技巧
(1)巧用相反向量:向量减法的三角形法则是解决空间向量加法、减法的关键,灵活运用相反向量可使向量首尾相接.
(2)巧用平移:利用三角形法则和平行四边形法则进行向量加、减法运算时,务必注意和向量、差向量的方向,必要时可采用空间向量的自由平移获得运算结果.
2.利用数乘运算进行向量表示的技巧
(1)数形结合:利用数乘运算解题时,要结合具体图形,利用三角形法则、平行四边形法则,将目标向量转化为已知向量.
(2)明确目标:在化简过程中要有目标意识,巧妙运用中点性质.
要点辨析
典例2、(1)如图所示,在正方体中,下列各式中运算结果为向量的有( )
①;②;
③;④.
A.1个 B.2个 C.3个 D.4个
思路
本题考查空间向量中,根据向量的三角形法则以及三角形中位线的性质,依次得出空间向量加法的运算结果.
分析计算能力
典型例题
典例2、(1)如图所示,在正方体中,下列各式中运算结果为向量的有( )
①;②;
③;④.
A.1个 B.2个 C.3个 D.4个
分析计算能力
典型例题
解析
(1)对于①,(;
对于②,;
对于③,;
对于④,.
D
典例2、(2)已知空间四边形,连接,,设,分别是,的中点,则等于( )
A. B.3 C.3 D.
分析计算能力
典型例题
解析
答案B
B
探究点3 空间向量的共线问题
共线向量定理:对于空间任意两个向量的充要条件是存在实数使.
证明空间三点共线的三种思路:对于空间三点可通过证明下列结论来证明三点共线.
(1)存在实数,使成立.
(2)对空间任一点,有.
(3)对空间任一点,有.
要点辨析
典例3、若非零空间向量不共线,则使与共线的的值为_______________.
思路
本题考查空间向量中,根据空间向量的共线向量定理,找出唯一的实数,计算得出值.
分析计算能力
典型例题
解析
若与共线,则,
.答案
探究点4 空间向量的共面问题
1.共面向量:平行于同一个平面的向量叫做共面向量.
2.共面向量定理:若两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对,使.
四点共面的结论:
(1)存在有序实数对,使得,
(2)空间一点在平面内的充要条件是存在有序实数组使得(其中).
(3)四点中任意两点的方向向量与另外两点的方向向量共线,如.
要点辨析
典例4、 [分析计算能力]已知向量不共面,且,试判断是否共面.
思路
本题考查空间向量中,根据空间向量的共面向量定理解决问题,首先设,然后用分别表示出,通过系数相等算出.
分析计算能力
典型例题
解析
解:设,即.
因为不共面,所以,
而此方程组无解,所以不能用表示,即不共面.
探究点5 空间向量的数量积运算
1.(1)夹角的定义
已知两个非零向量与,在空间任取一点,作,则叫做向量与的夹角,记作.
(2)范围:空间向量的夹角范围是.
2.(1)空间向量的数量积定义:已知两个非零向量,则叫做的数量积,记作,即.
(2)数量积的运算律
数乘向量与数量积的结合律
交换律
分配律
1.两个向量的数量积是数量,而不是向量,它可以是正数、负数或零.
2.向量数量积的运算不满足消去律、作商和乘法的结合律.
3.可利用数量积证明垂直,计算夹角,计算距离.
要点辨析
典例4、如图所示,在一个直二面角的棱上有两点,,,分别是这个二面角的两个面内垂直于的线段,且,,,则的长为__________.
思路
本题考查空间向量中,根据空间向量的数量积解决问题,首先,将用其他向量表示出来,然后利用模的算法计算的模.
分析计算能力
典型例题
解析
,
.
人教A版同步教材名师课件
空间向量及其运算
---知识探究
1.空位向量:在空间,具有大小和方向的量叫做空间向量.
2.长度或模:空间向量的大小.
3.表示方法
(1)几何表示法:空间向量用有向线段表示.
(2)字母表示法:用字母表示;若向量的起点是,终点是,也可记作:,其模记为或.
(3)坐标表示法:建立空间坐标系后,还可以用坐标表示空间向量.
4.常见的特殊向量
(1)零向量:长度为0的向量叫做零向量,记为0.
(2)单位向量:模为1的向量叫做单位向量.
探究点1 空间向量的相关概念
(3)相反向量:与向量长度相等而方向相反的向量,叫做的相反向量,记为.
(4)共线向量:如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量.
(5)方向向量:在直线上取非零向量,与向量平行的非零向量称为直线的方向向量.
(6)相等向量:方向相同且模相等的向量叫做相等向量.
探究点1 空间向量的相关概念
1.空间向量要紧紧抓住向量的两个要素,即大小和方向.
2.注意一些特殊向量的特性
(1)零向量不是没有方向,而是它的方向是任意的,且与任何向量都共线,这一点说明了共线向量不具备传递性.
(2)单位向量方向虽然不一定相同,但它们的长度都是1.
(3)两个向量模相等,不一定是相等向量;反之,若两个向量相等,则它们不仅模相等,方向也相同.若两个向量模相等,方向相反,则它们为相反向量.
要点辨析
典例1、给出下列命题:
①若,则或;
②若向量是向量的相反向量,则;
③在正方体中,;
④若空间向量满足,则.其中正确命题的序号是___________.
思路
本题考查空间向量的相关概念和常见的特殊向量的定义,根据向量的概念,向量既有大小,又有方向,所以要从两方面来判断关于空间向量的有关概念的题目;模相等的向量,方向不一定相同或相反,而相反向量的模一定相等,空间向量是自由向量,所以只要模相等,方向在一条直线或平行就可以判断两个相等或相反.
概括理解能力
典型例题
典例1、给出下列命题:
①若,则或;
②若向量是向量的相反向量,则;
③在正方体中,;
④若空间向量满足,则.其中正确命题的序号是___________.
概括理解能力
典型例题
解析
对于①,向量与的方向不一定相同或相反,故①错;
对于②,根据相反向量的定义知,故②正确;
对于③,根据相等向量的定义知,,故③正确;
对于④,根据相等向量的定义知正确.答案②③④.
②③④
1.向量的加法、减法运算
探究点2 空间向量的线性运算
空间向量的运算 加法
减法
加法运算律 ①交换律: ②结合律:
探究点2 空间向量的线性运算
2.空间向量的数乘运算
(1)定义:实数与空间向量的乘积仍然是一个向量,称为向量的数乘运算.
当时,与向量方向相同;当时,与向量方向相反; 的长度是的长度的倍.
(2)运算律
①结合律:.
②分配律:.
1.空间向量加法、减法运算的两个技巧
(1)巧用相反向量:向量减法的三角形法则是解决空间向量加法、减法的关键,灵活运用相反向量可使向量首尾相接.
(2)巧用平移:利用三角形法则和平行四边形法则进行向量加、减法运算时,务必注意和向量、差向量的方向,必要时可采用空间向量的自由平移获得运算结果.
2.利用数乘运算进行向量表示的技巧
(1)数形结合:利用数乘运算解题时,要结合具体图形,利用三角形法则、平行四边形法则,将目标向量转化为已知向量.
(2)明确目标:在化简过程中要有目标意识,巧妙运用中点性质.
要点辨析
典例2、(1)如图所示,在正方体中,下列各式中运算结果为向量的有( )
①;②;
③;④.
A.1个 B.2个 C.3个 D.4个
思路
本题考查空间向量中,根据向量的三角形法则以及三角形中位线的性质,依次得出空间向量加法的运算结果.
分析计算能力
典型例题
典例2、(1)如图所示,在正方体中,下列各式中运算结果为向量的有( )
①;②;
③;④.
A.1个 B.2个 C.3个 D.4个
分析计算能力
典型例题
解析
(1)对于①,(;
对于②,;
对于③,;
对于④,.
D
典例2、(2)已知空间四边形,连接,,设,分别是,的中点,则等于( )
A. B.3 C.3 D.
分析计算能力
典型例题
解析
答案B
B
探究点3 空间向量的共线问题
共线向量定理:对于空间任意两个向量的充要条件是存在实数使.
证明空间三点共线的三种思路:对于空间三点可通过证明下列结论来证明三点共线.
(1)存在实数,使成立.
(2)对空间任一点,有.
(3)对空间任一点,有.
要点辨析
典例3、若非零空间向量不共线,则使与共线的的值为_______________.
思路
本题考查空间向量中,根据空间向量的共线向量定理,找出唯一的实数,计算得出值.
分析计算能力
典型例题
解析
若与共线,则,
.答案
探究点4 空间向量的共面问题
1.共面向量:平行于同一个平面的向量叫做共面向量.
2.共面向量定理:若两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对,使.
四点共面的结论:
(1)存在有序实数对,使得,
(2)空间一点在平面内的充要条件是存在有序实数组使得(其中).
(3)四点中任意两点的方向向量与另外两点的方向向量共线,如.
要点辨析
典例4、 [分析计算能力]已知向量不共面,且,试判断是否共面.
思路
本题考查空间向量中,根据空间向量的共面向量定理解决问题,首先设,然后用分别表示出,通过系数相等算出.
分析计算能力
典型例题
解析
解:设,即.
因为不共面,所以,
而此方程组无解,所以不能用表示,即不共面.
探究点5 空间向量的数量积运算
1.(1)夹角的定义
已知两个非零向量与,在空间任取一点,作,则叫做向量与的夹角,记作.
(2)范围:空间向量的夹角范围是.
2.(1)空间向量的数量积定义:已知两个非零向量,则叫做的数量积,记作,即.
(2)数量积的运算律
数乘向量与数量积的结合律
交换律
分配律
1.两个向量的数量积是数量,而不是向量,它可以是正数、负数或零.
2.向量数量积的运算不满足消去律、作商和乘法的结合律.
3.可利用数量积证明垂直,计算夹角,计算距离.
要点辨析
典例4、如图所示,在一个直二面角的棱上有两点,,,分别是这个二面角的两个面内垂直于的线段,且,,,则的长为__________.
思路
本题考查空间向量中,根据空间向量的数量积解决问题,首先,将用其他向量表示出来,然后利用模的算法计算的模.
分析计算能力
典型例题
解析
,
.
