21.3 实际问题与一元二次方程 第1课时传播与面积类问题 课件(共27张PPT)
文档属性
| 名称 | 21.3 实际问题与一元二次方程 第1课时传播与面积类问题 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 21:32:50 | ||
图片预览







文档简介
(共27张PPT)
第二十一章 一元二次方程
第1课时 传播、面积类问题
21.3 实际问题与一元二次方程
学习目标
1.会分析传播问题和面积问题中的数量关系并会列一元二次方程.(重点)
2.正确分析传播和面积问题中的数量关系.(难点)
3.会找出实际问题中的相等关系并建模解决问题.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
同一元一次方程、二元一次方程(组)等一样,一元二次方程也可以作为反映某些实际问题中数
量关系的数学模型.本节继续讨论如何利用一元
二次方程解决实际问题.
类比可知:列一元二次方程解应用题的步骤?
①审题, ②设出未知数,
③找等量关系, ④列方程,
⑤解方程, ⑥验根,
⑦答.
讲授新知
贰
讲授新知
知识点1 传播问题与一元二次方程
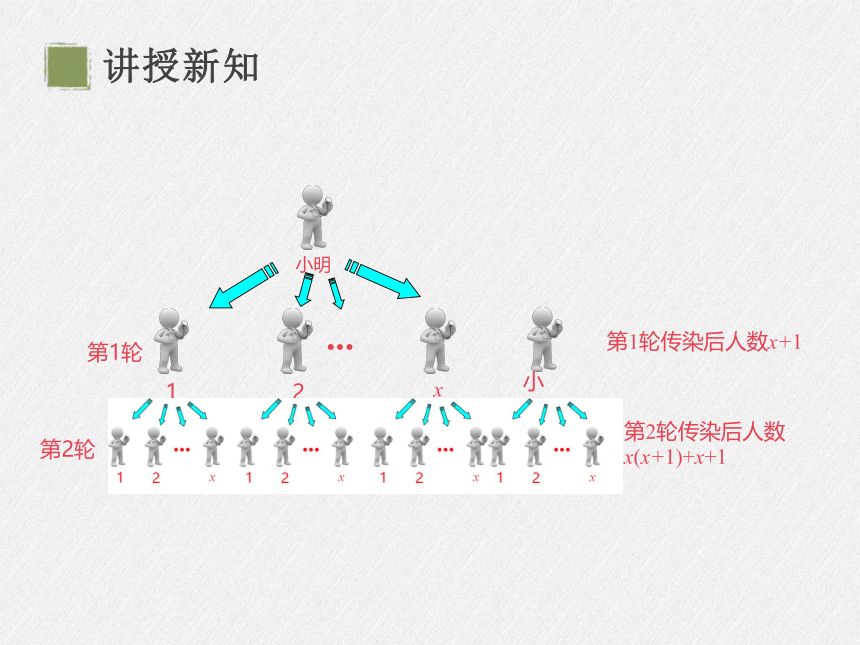
例1 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
分析:设每轮传染中平均一个人传染了x个人. 传染源记作小明,其传染示意图如下:
小明
第1轮
第1轮传染后人数x+1
第2轮传染后人数
x(x+1)+x+1
小明
1
2
x
第2轮
讲授新知
知识点
x1= , x2=
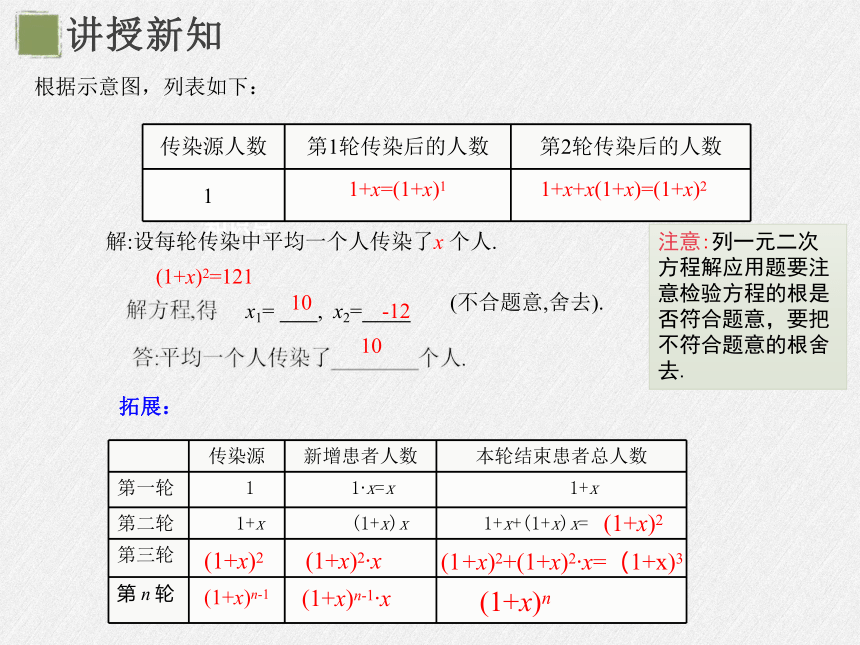
根据示意图,列表如下:
解方程,得
答:平均一个人传染了________个人.
10
-12
(不合题意,舍去).
10
解:设每轮传染中平均一个人传染了x 个人.
(1+x)2=121
传染源人数 第1轮传染后的人数 第2轮传染后的人数
1
1+x=(1+x)1
1+x+x(1+x)=(1+x)2
注意:列一元二次方程解应用题要注意检验方程的根是否符合题意,要把不符合题意的根舍去.
传染源 新增患者人数 本轮结束患者总人数
第一轮 1 1 x=x 1+x
第二轮 1+x (1+x)x 1+x+(1+x)x=
第三轮
第 n 轮
拓展:
(1+x)2
(1+x)2
(1+x)2 x
(1+x)2+(1+x)2 x=(1+x)3
(1+x)n-1
(1+x)n-1 x
(1+x)n
讲授新知
例2 某种电脑病毒传播速度非常快,如果一台电脑被感染,
经过两轮感染后就会有 100 台电脑被感染.请你用学过的知识
分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不
到有效控制,4 轮感染后,被感染的电脑会不会超过 7000 台?
解:设每轮感染中平均一台电脑会感染 x 台电脑,则
1+x+x(1+x)=100,即(1+x)2=100.
解得 x1=9,x2=-11(舍去).∴x=9.
4 轮感染后,被感染的电脑数为(1+x)4=104>7000.
答:每轮感染中平均每一台电脑会感染 9 台电脑,4 轮感染后,被感染的电脑会超过 7000 台.
范例应用
20
32
x
x
解:设道路的宽为x米
例3:如图,在一块宽为20m, 长为32m的矩形地面上修筑同样宽的两条道路,余下的部分种上草坪,要使草坪的面积为540㎡,求道路的宽为多少?
还有其他解法吗?
讲授新知
知识点2 面积问题与一元二次方程
20
32
x
x
解:设道路的宽为 x 米
20-x
32-x
(32-x)(20-x)=540
整理,得x2-52x+100=0
解得 x1=2,x2=50
当x=50时,32-x=-18,不合题意,舍去.
∴取x=2
答:道路的宽为2米.
方法二:
讲授新知
在宽为20m, 长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540㎡,求
这种方案下的道路的宽为多少?
解:设道路的宽为 x 米
(32-x)(20-x)=540
可列方程为
变式一
20
32
x
x
x
在宽为20m, 长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540m2,求这种种方案下的道路的宽为多少?
解:设道路的宽为 x 米
(32-2x)(20-x)=540
可列方程为
变式二
范例应用
20
32
x
x
x
x
20
32
2x
2x
32-2x
20-2x
在宽为20m, 长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540m2,求这种种方案下的道路的宽为多少?
解:设道路的宽为 x 米
(32-2x)(20-2x)=540
可列方程为
变式三
范例应用
在宽为20m, 长为32m的矩形地面上修筑四条道路,余下的部分种上草坪,如果横、纵小路的宽度比为3:2,且使小路所占面积是矩形面积的四分之一,求道路的宽为多少?
变式四
范例应用
小路所占面积是矩形面积的四分之一
剩余面积是矩形面积的四分之三
解:设横、竖小路的宽度分别为3x、 2x,
于是可列方程
(30-4x)(20-6x)= —×20×30
20㎝
30㎝
3x
2x
30-4x
20-6x
4
3
3x
2x
6x
4x
30-4x
20-6x
范例应用
当堂训练
叁
1.元旦将至,九年级一班全体学生互赠贺卡,共赠贺卡1980张,问九年级一班共有多少名学生?设九年级一班共有x名学生,那么所列方程为( )
A.x2=1980 B. x(x+1)=1980 C. x(x-1)=1980 D.x(x-1)=1980
2.有一根月季,它的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干、小分支的总数是73,设每个枝干长出x个小分支,根据题意可列方程为( )
A.1+x+x(1+x)=73 B.1+x+x2=73 C.1+x2 =73 D.(1+x)2=73
3.在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
D
B
当堂训练
B
当堂训练
4. 如图所示,某农场要建一个长方形的养鸡场,养鸡场的一边靠墙(墙长25m),另外三边用木栏围成,木栏长40m.则养鸡场的面积能达到180m2吗 如果能,请给出设计方案;如果不能,请说明理由.
解:设养鸡场的长为xm,根据题意得:
即 x2 - 40x + 360=0.
解方程,得 x1 = x2= (舍去),
答:鸡场的为( )m满足条件.
25m
180m2
解:设每天平均一个人传染了x人,
解得 x1=-4 (舍去),x2=2.
答:每天平均一个人传染了2人,这个地区一共将会有2187人患甲型流感.
1+x+x(1+x)=9,
即(1+x)2=9.
9(1+x)5=9(1+2)5=2187,
(1+x)7= (1+2)7=2187.
5.甲型流感病毒的传染性极强,某地因1人患了甲型流感没有及时隔离治疗,经过两天的传染后共有9人患了甲型流感,每天平均一个人传染了几人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型流感?
当堂训练
课堂小结
肆
列一元二次方程解应题
与列一元一次方程解决实际问题基本相同.不同的地方是要检验根的合理性.
传播问题
数量关系:
第一轮传播后的量=传播前的量× (1+传播速度)
第二轮传播后的量=第一轮传播后的量× (1+传播速度)=传播前的量× (1+传播速度)2
面积问题
常见几何图形面积是等量关系.
封面问题和小路宽带问题(用平移的思想)
步骤
类型
课堂小结
课后作业
基础题:1.课后习题P22 第 4,8,9题。
提高题:2.把今天所讲的4,5题在作业本上整理.
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第二十一章 一元二次方程
第1课时 传播、面积类问题
21.3 实际问题与一元二次方程
学习目标
1.会分析传播问题和面积问题中的数量关系并会列一元二次方程.(重点)
2.正确分析传播和面积问题中的数量关系.(难点)
3.会找出实际问题中的相等关系并建模解决问题.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
同一元一次方程、二元一次方程(组)等一样,一元二次方程也可以作为反映某些实际问题中数
量关系的数学模型.本节继续讨论如何利用一元
二次方程解决实际问题.
类比可知:列一元二次方程解应用题的步骤?
①审题, ②设出未知数,
③找等量关系, ④列方程,
⑤解方程, ⑥验根,
⑦答.
讲授新知
贰
讲授新知
知识点1 传播问题与一元二次方程
例1 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
分析:设每轮传染中平均一个人传染了x个人. 传染源记作小明,其传染示意图如下:
小明
第1轮
第1轮传染后人数x+1
第2轮传染后人数
x(x+1)+x+1
小明
1
2
x
第2轮
讲授新知
知识点
x1= , x2=
根据示意图,列表如下:
解方程,得
答:平均一个人传染了________个人.
10
-12
(不合题意,舍去).
10
解:设每轮传染中平均一个人传染了x 个人.
(1+x)2=121
传染源人数 第1轮传染后的人数 第2轮传染后的人数
1
1+x=(1+x)1
1+x+x(1+x)=(1+x)2
注意:列一元二次方程解应用题要注意检验方程的根是否符合题意,要把不符合题意的根舍去.
传染源 新增患者人数 本轮结束患者总人数
第一轮 1 1 x=x 1+x
第二轮 1+x (1+x)x 1+x+(1+x)x=
第三轮
第 n 轮
拓展:
(1+x)2
(1+x)2
(1+x)2 x
(1+x)2+(1+x)2 x=(1+x)3
(1+x)n-1
(1+x)n-1 x
(1+x)n
讲授新知
例2 某种电脑病毒传播速度非常快,如果一台电脑被感染,
经过两轮感染后就会有 100 台电脑被感染.请你用学过的知识
分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不
到有效控制,4 轮感染后,被感染的电脑会不会超过 7000 台?
解:设每轮感染中平均一台电脑会感染 x 台电脑,则
1+x+x(1+x)=100,即(1+x)2=100.
解得 x1=9,x2=-11(舍去).∴x=9.
4 轮感染后,被感染的电脑数为(1+x)4=104>7000.
答:每轮感染中平均每一台电脑会感染 9 台电脑,4 轮感染后,被感染的电脑会超过 7000 台.
范例应用
20
32
x
x
解:设道路的宽为x米
例3:如图,在一块宽为20m, 长为32m的矩形地面上修筑同样宽的两条道路,余下的部分种上草坪,要使草坪的面积为540㎡,求道路的宽为多少?
还有其他解法吗?
讲授新知
知识点2 面积问题与一元二次方程
20
32
x
x
解:设道路的宽为 x 米
20-x
32-x
(32-x)(20-x)=540
整理,得x2-52x+100=0
解得 x1=2,x2=50
当x=50时,32-x=-18,不合题意,舍去.
∴取x=2
答:道路的宽为2米.
方法二:
讲授新知
在宽为20m, 长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540㎡,求
这种方案下的道路的宽为多少?
解:设道路的宽为 x 米
(32-x)(20-x)=540
可列方程为
变式一
20
32
x
x
x
在宽为20m, 长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540m2,求这种种方案下的道路的宽为多少?
解:设道路的宽为 x 米
(32-2x)(20-x)=540
可列方程为
变式二
范例应用
20
32
x
x
x
x
20
32
2x
2x
32-2x
20-2x
在宽为20m, 长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540m2,求这种种方案下的道路的宽为多少?
解:设道路的宽为 x 米
(32-2x)(20-2x)=540
可列方程为
变式三
范例应用
在宽为20m, 长为32m的矩形地面上修筑四条道路,余下的部分种上草坪,如果横、纵小路的宽度比为3:2,且使小路所占面积是矩形面积的四分之一,求道路的宽为多少?
变式四
范例应用
小路所占面积是矩形面积的四分之一
剩余面积是矩形面积的四分之三
解:设横、竖小路的宽度分别为3x、 2x,
于是可列方程
(30-4x)(20-6x)= —×20×30
20㎝
30㎝
3x
2x
30-4x
20-6x
4
3
3x
2x
6x
4x
30-4x
20-6x
范例应用
当堂训练
叁
1.元旦将至,九年级一班全体学生互赠贺卡,共赠贺卡1980张,问九年级一班共有多少名学生?设九年级一班共有x名学生,那么所列方程为( )
A.x2=1980 B. x(x+1)=1980 C. x(x-1)=1980 D.x(x-1)=1980
2.有一根月季,它的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干、小分支的总数是73,设每个枝干长出x个小分支,根据题意可列方程为( )
A.1+x+x(1+x)=73 B.1+x+x2=73 C.1+x2 =73 D.(1+x)2=73
3.在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
D
B
当堂训练
B
当堂训练
4. 如图所示,某农场要建一个长方形的养鸡场,养鸡场的一边靠墙(墙长25m),另外三边用木栏围成,木栏长40m.则养鸡场的面积能达到180m2吗 如果能,请给出设计方案;如果不能,请说明理由.
解:设养鸡场的长为xm,根据题意得:
即 x2 - 40x + 360=0.
解方程,得 x1 = x2= (舍去),
答:鸡场的为( )m满足条件.
25m
180m2
解:设每天平均一个人传染了x人,
解得 x1=-4 (舍去),x2=2.
答:每天平均一个人传染了2人,这个地区一共将会有2187人患甲型流感.
1+x+x(1+x)=9,
即(1+x)2=9.
9(1+x)5=9(1+2)5=2187,
(1+x)7= (1+2)7=2187.
5.甲型流感病毒的传染性极强,某地因1人患了甲型流感没有及时隔离治疗,经过两天的传染后共有9人患了甲型流感,每天平均一个人传染了几人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型流感?
当堂训练
课堂小结
肆
列一元二次方程解应题
与列一元一次方程解决实际问题基本相同.不同的地方是要检验根的合理性.
传播问题
数量关系:
第一轮传播后的量=传播前的量× (1+传播速度)
第二轮传播后的量=第一轮传播后的量× (1+传播速度)=传播前的量× (1+传播速度)2
面积问题
常见几何图形面积是等量关系.
封面问题和小路宽带问题(用平移的思想)
步骤
类型
课堂小结
课后作业
基础题:1.课后习题P22 第 4,8,9题。
提高题:2.把今天所讲的4,5题在作业本上整理.
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
