人教A版(2019)高中数学选择性必修第一册《空间向量的数量积运算》名师课件(共28张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册《空间向量的数量积运算》名师课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 22:25:04 | ||
图片预览






文档简介
(共28张PPT)
平面向量数量积的定义
已知两个非零向量和,它们的夹角为 ,我们把数量 叫做与的数量积 (或内积),记作.
规定:零向量与任意向量的数量积为0.
复习引入
人教A版同步教材名师课件
空间向量的数量积运算
学习目标
学 习 目 标 核心素养
掌握空间向量数量积的定义及运算律 数学抽象
数学运算
利用空间向量的数量积解决夹角问题 数学抽象
数学运算
学习目标
学习目标:
1.掌握空间向量夹角的概念及表示方法
2.掌握空间向量的数量积的定义、性质、运算律及计算方法
3.掌握投影向量的概念
4.能用向量的数量积解决立体几何问题
学科核心素养:
1.通过学习空间向量的数量积运算,培养学生数学运算的核心素养.
2.借助投影向量概念的学习,培养学生直观想象和逻辑推理的核心素养.
3.借助利用空间向量数量积证明垂直关系、求夹角和距离运算,提升学生的逻辑推理和数学运算核心素养.
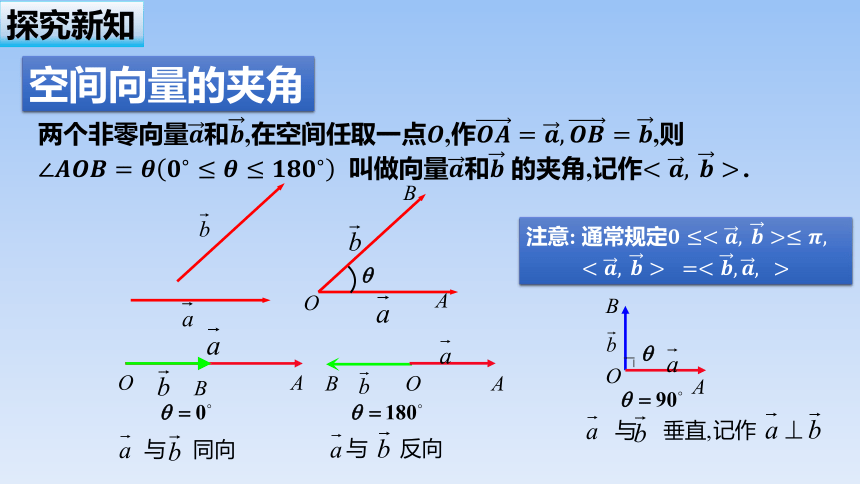
两个非零向量和,在空间任取一点,作,则 叫做向量和 的夹角,记作.
与 反向
O
A
B
O
A
与 同向
O
A
B
B
记作
与 垂直,
O
A
B
注意: 通常规定
空间向量的夹角
探究新知
空间向量数量积的定义:
已知两个非零向量和,则叫做与的数量积 (或内积),记作.
规定:零向量与任意向量的数量积为0.
探究新知
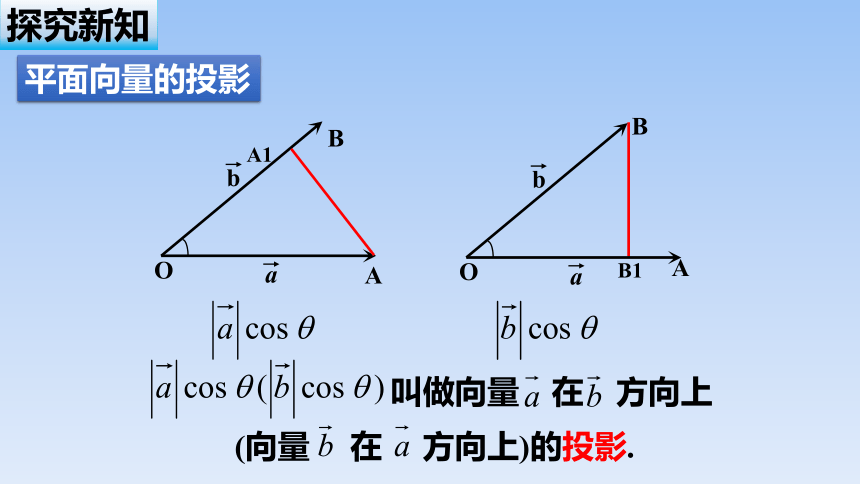
平面向量的投影
B1
O
A
B
b
a
A1
O
A
B
b
a
叫做向量 在 方向上(向量 在 方向上)的投影.
探究新知
向量在向量上的投影是数量,不是向量,什么时候为正,什么时候为负?
O
A
B
O
A
B
B
O
A
O
A
B
O
A
B
探究新知
探究新知
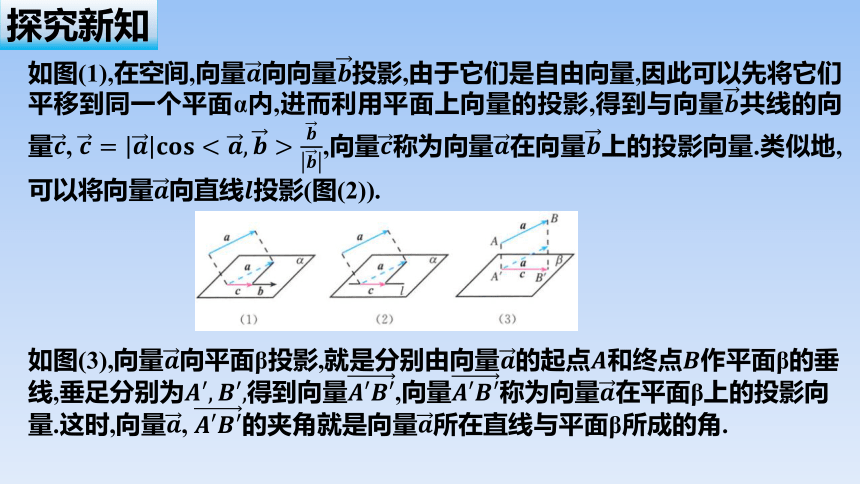
如图(1),在空间,向量向向量投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量共线的向量, ,向量称为向量在向量上的投影向量.类似地,可以将向量向直线投影(图(2)).
如图(3),向量向平面β投影,就是分别由向量的起点和终点作平面β的垂线,垂足分别为得到向量,向量称为向量在平面β上的投影向量.这时,向量, 的夹角就是向量所在直线与平面β所成的角.
探究新知
数乘向量与数量积的结合律
交换律
分配律
空间向量的数量积满足如下的运算律
思考2:对于向量,若等式·,能不能写成
(或)?为什么?
思考1:对于非零向量,若·= ·,那么=吗?
探究新知
思考3:对于非零向量,,(·)··(·)成立吗?为什么?
(·)·≠ ·(·)
不能,向量没有除法运算
·= ·=,如右图示
典例讲解
例1、已知长方体中,为侧面的中心,为的中点.
求下列向量的数量积:
.
如图所示,设
则| |=| |=2,| |=4, · = · = · =0.
(1) = ·(+ )=.
=
变式训练
典例讲解
例1、已知长方体中,为侧面的中心,为的中点.
计算
(1)首先将各向量分解成已知模和夹角的向量的组合形式.
在几何体中求空间向量数量积的步骤
(2)利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积.
(3)代入a·b=|a||b|cos求解.
方法归纳
1.(1)已知||=3,||=4,<>=120°,则(3-2)·(+2)=________.
(2)如图,已知正四面体OABC的棱长为1.求:
① ;② .
-61
变式训练
(1)(3-2)·(+2)
(2)在正四面体中, .
①
②
例2、如图所示,已知是边长为1的正△所在平面外一点,且分别是的中点,设.
(1)试用表示;
(2)求的值;
(3)求异面直线与所成角的余弦值.
典例讲解
(1)由题意,得,且三个向量两两夹角均为,故.
(2)由(1)知
例2、如图所示,已知是边长为1的正△所在平面外一点,且分别是的中点,设.
(1)试用表示;
(2)求的值;
(3)求异面直线与所成角的余弦值.
典例讲解
(3)由于,所以异面直线与所成角的余弦值为.
利用向量数量积求夹角问题的思路
(1)求两个向量的夹角有两种方法:
方法归纳
①结合图形,平移向量,利用空间向量的夹角定义来求,但要注意向量夹角的范围;
②先求,再利用公式,求cos ,最.
(2) 求两条异面直线所成的角,步骤如下:
①根据题设条件在所求的异面直线上取两个向量(即直线的方向向量);
②异面直线所成角的问题转化为向量夹角问题;
③利用数量积求余弦值或角的大小;
④异面直线所成的角为锐角或直角,利用向量数量积求夹角余弦值应将余弦值加上绝对值,进而求出角的大小.
利用向量数量积求夹角问题的思路
方法归纳
变式训练
2.(1)已知为单位向量,且,若,,则实数的值为( )
A.-6 B.6 C.3 D.-3
(2)如图,在正方体中,异面直线与所
成的角为 .
(3)如图所示,正四面体的每条棱长都等于,点
分别是的中点,求证:.
由题意可得,所以,所以,所以.
B
设正方体的棱长为1,则,
.
又,所以,
所以异面直线与所成的角为.
变式训练
2.(1)已知为单位向量,且,若,,则实数的值为( )
A.-6 B.6 C.3 D.-3
(2)如图,在正方体中,异面直线与所
成的角为 .
(3)如图所示,正四面体的每条棱长都等于,点
分别是的中点,求证:.
B
(3)
所以同理可证.
例3、正三棱柱(底面是正三角形的直三棱柱)ABC -A1B1C1的各棱长都为2,E、F分别是AB、A1C1的中点,求EF的长.
典例讲解
如图所示,设.由题意知,且.
求两点间的距离或线段的长度的方法
方法归纳
(1)将此线段用向量表示;
(2)用其他已知夹角和模的向量表示该向量;
(3)利用,计算出,即得所求距离.
素养提炼
1.空间向量数量积性质的应用
(1)a⊥b a·b=0,此结论用于证明空间中的垂直关系.
(2)|a|2=a2,此结论用于求空间中线段的长度.
(3)cos =,此结论用于求有关空间角的问题.
(4)|b|cos=,此结论用于求空间中的距离问题.
素养提炼
2.空间向量的数量积的三点注意
(1)数量积的符号由夹角的余弦值决定.
(2)当a≠0时,由a·b=0可得a⊥b或b=0.
(3)空间向量没有除法运算:即若a·b=k,则没有a=.
素养提炼
3.向量夹角与异面直线的关系
若两个向量a,b所在直线为异面直线,两异面直线所成的角为θ,则
(1)向量夹角的范围是0<<π,异面直线的夹角θ的范围是0<θ≤.
(2)当两向量的夹角为锐角时,θ= ;当两向量的夹角为时,两异面直线垂直;当两向量的夹角为钝角时,θ=π- .
通过学习,体会到我们可以利用向量数量积解决立体几何中的以下问题:
1、解决直线垂直、线面垂直;
2、求两点之间的距离或线段长度;
3、求两直线所成角的余弦值等等.
归纳小结
P8 练习:2、3、4
作 业
平面向量数量积的定义
已知两个非零向量和,它们的夹角为 ,我们把数量 叫做与的数量积 (或内积),记作.
规定:零向量与任意向量的数量积为0.
复习引入
人教A版同步教材名师课件
空间向量的数量积运算
学习目标
学 习 目 标 核心素养
掌握空间向量数量积的定义及运算律 数学抽象
数学运算
利用空间向量的数量积解决夹角问题 数学抽象
数学运算
学习目标
学习目标:
1.掌握空间向量夹角的概念及表示方法
2.掌握空间向量的数量积的定义、性质、运算律及计算方法
3.掌握投影向量的概念
4.能用向量的数量积解决立体几何问题
学科核心素养:
1.通过学习空间向量的数量积运算,培养学生数学运算的核心素养.
2.借助投影向量概念的学习,培养学生直观想象和逻辑推理的核心素养.
3.借助利用空间向量数量积证明垂直关系、求夹角和距离运算,提升学生的逻辑推理和数学运算核心素养.
两个非零向量和,在空间任取一点,作,则 叫做向量和 的夹角,记作.
与 反向
O
A
B
O
A
与 同向
O
A
B
B
记作
与 垂直,
O
A
B
注意: 通常规定
空间向量的夹角
探究新知
空间向量数量积的定义:
已知两个非零向量和,则叫做与的数量积 (或内积),记作.
规定:零向量与任意向量的数量积为0.
探究新知
平面向量的投影
B1
O
A
B
b
a
A1
O
A
B
b
a
叫做向量 在 方向上(向量 在 方向上)的投影.
探究新知
向量在向量上的投影是数量,不是向量,什么时候为正,什么时候为负?
O
A
B
O
A
B
B
O
A
O
A
B
O
A
B
探究新知
探究新知
如图(1),在空间,向量向向量投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量共线的向量, ,向量称为向量在向量上的投影向量.类似地,可以将向量向直线投影(图(2)).
如图(3),向量向平面β投影,就是分别由向量的起点和终点作平面β的垂线,垂足分别为得到向量,向量称为向量在平面β上的投影向量.这时,向量, 的夹角就是向量所在直线与平面β所成的角.
探究新知
数乘向量与数量积的结合律
交换律
分配律
空间向量的数量积满足如下的运算律
思考2:对于向量,若等式·,能不能写成
(或)?为什么?
思考1:对于非零向量,若·= ·,那么=吗?
探究新知
思考3:对于非零向量,,(·)··(·)成立吗?为什么?
(·)·≠ ·(·)
不能,向量没有除法运算
·= ·=,如右图示
典例讲解
例1、已知长方体中,为侧面的中心,为的中点.
求下列向量的数量积:
.
如图所示,设
则| |=| |=2,| |=4, · = · = · =0.
(1) = ·(+ )=.
=
变式训练
典例讲解
例1、已知长方体中,为侧面的中心,为的中点.
计算
(1)首先将各向量分解成已知模和夹角的向量的组合形式.
在几何体中求空间向量数量积的步骤
(2)利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积.
(3)代入a·b=|a||b|cos
方法归纳
1.(1)已知||=3,||=4,<>=120°,则(3-2)·(+2)=________.
(2)如图,已知正四面体OABC的棱长为1.求:
① ;② .
-61
变式训练
(1)(3-2)·(+2)
(2)在正四面体中, .
①
②
例2、如图所示,已知是边长为1的正△所在平面外一点,且分别是的中点,设.
(1)试用表示;
(2)求的值;
(3)求异面直线与所成角的余弦值.
典例讲解
(1)由题意,得,且三个向量两两夹角均为,故.
(2)由(1)知
例2、如图所示,已知是边长为1的正△所在平面外一点,且分别是的中点,设.
(1)试用表示;
(2)求的值;
(3)求异面直线与所成角的余弦值.
典例讲解
(3)由于,所以异面直线与所成角的余弦值为.
利用向量数量积求夹角问题的思路
(1)求两个向量的夹角有两种方法:
方法归纳
①结合图形,平移向量,利用空间向量的夹角定义来求,但要注意向量夹角的范围;
②先求,再利用公式,求cos ,最.
(2) 求两条异面直线所成的角,步骤如下:
①根据题设条件在所求的异面直线上取两个向量(即直线的方向向量);
②异面直线所成角的问题转化为向量夹角问题;
③利用数量积求余弦值或角的大小;
④异面直线所成的角为锐角或直角,利用向量数量积求夹角余弦值应将余弦值加上绝对值,进而求出角的大小.
利用向量数量积求夹角问题的思路
方法归纳
变式训练
2.(1)已知为单位向量,且,若,,则实数的值为( )
A.-6 B.6 C.3 D.-3
(2)如图,在正方体中,异面直线与所
成的角为 .
(3)如图所示,正四面体的每条棱长都等于,点
分别是的中点,求证:.
由题意可得,所以,所以,所以.
B
设正方体的棱长为1,则,
.
又,所以,
所以异面直线与所成的角为.
变式训练
2.(1)已知为单位向量,且,若,,则实数的值为( )
A.-6 B.6 C.3 D.-3
(2)如图,在正方体中,异面直线与所
成的角为 .
(3)如图所示,正四面体的每条棱长都等于,点
分别是的中点,求证:.
B
(3)
所以同理可证.
例3、正三棱柱(底面是正三角形的直三棱柱)ABC -A1B1C1的各棱长都为2,E、F分别是AB、A1C1的中点,求EF的长.
典例讲解
如图所示,设.由题意知,且.
求两点间的距离或线段的长度的方法
方法归纳
(1)将此线段用向量表示;
(2)用其他已知夹角和模的向量表示该向量;
(3)利用,计算出,即得所求距离.
素养提炼
1.空间向量数量积性质的应用
(1)a⊥b a·b=0,此结论用于证明空间中的垂直关系.
(2)|a|2=a2,此结论用于求空间中线段的长度.
(3)cos
(4)|b|cos
素养提炼
2.空间向量的数量积的三点注意
(1)数量积的符号由夹角的余弦值决定.
(2)当a≠0时,由a·b=0可得a⊥b或b=0.
(3)空间向量没有除法运算:即若a·b=k,则没有a=.
素养提炼
3.向量夹角与异面直线的关系
若两个向量a,b所在直线为异面直线,两异面直线所成的角为θ,则
(1)向量夹角的范围是0<
(2)当两向量的夹角为锐角时,θ=
通过学习,体会到我们可以利用向量数量积解决立体几何中的以下问题:
1、解决直线垂直、线面垂直;
2、求两点之间的距离或线段长度;
3、求两直线所成角的余弦值等等.
归纳小结
P8 练习:2、3、4
作 业
