人教A版(2019)高中数学选择性必修第一册 1.1空间向量及其运算、空间向量基本定理 练习(含解析)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 1.1空间向量及其运算、空间向量基本定理 练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1003.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 22:33:07 | ||
图片预览




文档简介
空间向量及其运算、空间向量基本定理
一、单选题
1.(2019·全国高二课时练习)已知,,是不共面的三个向量,则能构成一个基底的一组向量是( )
A.2,﹣,+2 B.2,﹣,+2
C.,2,﹣ D.,+,﹣
2.(2020·贵州省铜仁第一中学高二开学考试)如图所示,在平行六面体中,设,,,是的中点,试用,,表示( )
A. B. C. D.
3.(2020·山东省章丘四中高二月考)如图,在四面体中,是的中点,是的中点,则等于( )
A. B.
C. D.
4.(2020·河南省高二期末)如图在平行六面体中,为的中点,设,,,则( )
A. B. C. D.
5.(2020·广东省红岭中学高二期末) 与共线是直线AB∥CD的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.(2020·广东省红岭中学高二期末)为空间任意一点,三点不共线,若=,则四点
A.一定不共面 B.不一定共面
C.一定共面 D.无法判断
7.(2019·随州市第一中学高二期中)空间四点共面,但任意三点不共线,若为该平面外一点且,则实数的值为( )
A. B. C. D.
8.(2020·甘肃省高二期末)如图,空间四边形OABC中,,,,且,,则等于( )
A. B.
C. D.
9.(2020·广西壮族自治区高二期末)在平行六面体中,为与的交点.若,,,则下列向量中与相等的向量是( ).
A. B. C. D.
10.(2019·新疆维吾尔自治区阿克苏市实验中学高二月考)在平行六面体ABCD-EFGH中,若=x﹣2y+3z,,则x+y+z等于( )
A. B. C. D.1
二、多选题
11.(2019·山东省济南一中高二期中)已知平行六面体,则下列四式中其中正确的有( )
A. B.
C. D.
12.(2020·江苏省高二期末)如图,在正方体中,下列各式中运算的结果为的有( )
A. B.
C. D.
13.(2020·山东省高二期末)已知A,B,C三点不共线,O为平面ABC外的任一点,则“点M与点A,B,C共面”的充分条件的是( )
A. B.
C. D.
三、填空题
14.(2019·江苏省高二期末)直三棱柱中,若,则__________.
15.(2019·新疆维吾尔自治区阿克苏市实验中学高二月考)已知非零向量,,且=+,+,,则中一定共线的三点是________.
16.(2019·浙江省诸暨中学高二期中)已知三棱锥O-ABC,点D是BC中点,P是AD中点,设,则________;x=________.
17.(2019·江苏省高二期中)如图在正方体中,已知,,,为底面的的中心,为的重心,则______
四、解答题
18.(2018·全国高二课时练习)如图,在长方体ABCD-A1B1C1D1中,AB=3,AD=2,AA1=1,以长方体的八个顶点中的两点为起点和终点的向量中.
(1)单位向量共有多少个
(2)试写出模为的所有向量.
(3)试写出与相等的所有向量.
(4)试写出的相反向量.
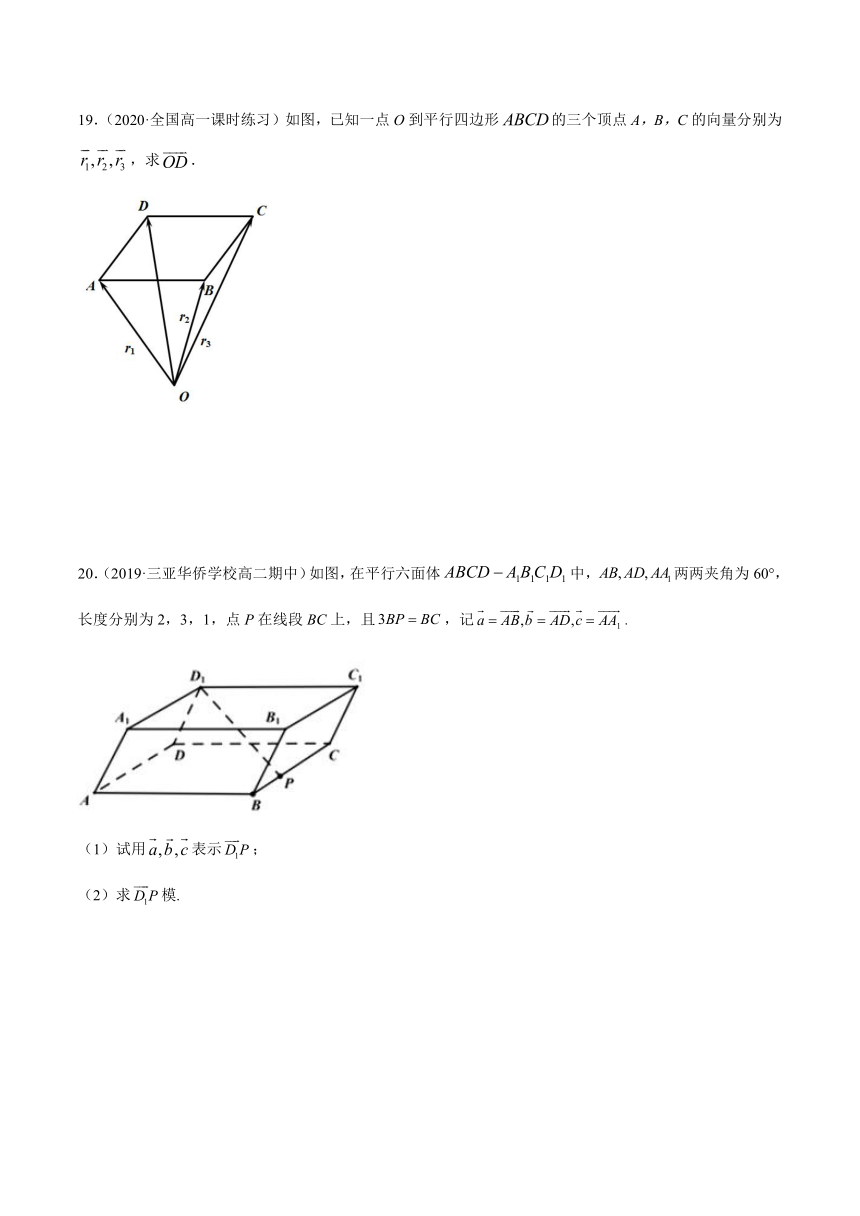
19.(2020·全国高一课时练习)如图,已知一点O到平行四边形的三个顶点A,B,C的向量分别为,求.
20.(2019·三亚华侨学校高二期中)如图,在平行六面体中,两两夹角为60°,长度分别为2,3,1,点P在线段BC上,且,记.
(1)试用表示;
(2)求模.
21.(2018·全国高二课时练习)在四棱锥P-ABCD中,ABCD为平行四边形,AC与BD交于O,G为BD上一点,BG=2GD,=,= ,= ,试用基底{,,}表示向量.
22.(2019·全国高一课时练习)设e1,e2是不共线的空间向量,已知=2e1+ke2,=e1+3e2,=2e1-e2.若A,B,D三点共线,求k的值.
23.(2018·全国高二课时练习)已知{e1,e2,e3}是空间的一个基底,=e1+2e2-e3,=-3e1+e2+2e3,=e1+e2-e3,试判断{}能否作为空间的一个基底 若能,试以此基底表示向量=2e1-e2+3e3;若不能,请说明理由.
空间向量及其运算、空间向量基本定理答案
一、单选题
1.(2019·全国高二课时练习)已知,,是不共面的三个向量,则能构成一个基底的一组向量是( )
A.2,﹣,+2 B.2,﹣,+2
C.,2,﹣ D.,+,﹣
【答案】C
【解析】
对于A,因为2=(﹣)+(+2),得2、﹣、+2三个向量共面,故它们不能构成一个基底,A不正确;
对于B,因为2=(﹣)+(+2),得2、﹣、+2三个向量共面,故它们不能构成一个基底,B不正确;
对于C,因为找不到实数λ、μ,使=λ 2+μ(﹣)成立,故、2、﹣三个向量不共面,
它们能构成一个基底,C正确;
对于D,因为=(+)﹣(﹣),得、+、﹣三个向量共面,故它们不能构成一个基底,D不正确
故选:C.
2.(2020·贵州省铜仁第一中学高二开学考试)如图所示,在平行六面体中,设,,,是的中点,试用,,表示( )
A. B. C. D.
【答案】A
【解析】
是的中点,
.
故选:A.
3.(2020·山东省章丘四中高二月考)如图,在四面体中,是的中点,是的中点,则等于( )
A. B.
C. D.
【答案】C
【解析】
在四面体中,是的中点,是的中点
故选:C.
4.(2020·河南省高二期末)如图在平行六面体中,为的中点,设,,,则( )
A. B. C. D.
【答案】A
【解析】
由题意结合平行六面体的性质可得
.
故选:A.
5.(2020·广东省红岭中学高二期末) 与共线是直线AB∥CD的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】B
【解析】
根据向量共线的定义,可知若与共线,则它们所在的直线可能平行,也可能重合;若AB∥CD,则与共线;根据充分条件和必要条件的概念,可知与共线是直线AB∥CD的必要不充分条件,
故选B
点睛:向量共线的定义:如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量 .
6.(2020·广东省红岭中学高二期末)为空间任意一点,三点不共线,若=,则四点
A.一定不共面 B.不一定共面
C.一定共面 D.无法判断
【答案】C
【解析】:点P在平面ABC内,O是平面ABC外的任意一点,则且.利用此推论可直接证明一定共面.
详解:因为=,且,所以四点共面.
7.(2019·随州市第一中学高二期中)空间四点共面,但任意三点不共线,若为该平面外一点且,则实数的值为( )
A. B. C. D.
【答案】A
【解析】因为空间四点共面,但任意三点不共线,对于该平面外一点都有,所以,解得.故选A
8.(2020·甘肃省高二期末)如图,空间四边形OABC中,,,,且,,则等于( )
A. B.
C. D.
【答案】C
【解析】
,,,,
,故选:C.
9.(2020·广西壮族自治区高二期末)在平行六面体中,为与的交点.若,,,则下列向量中与相等的向量是( ).
A. B. C. D.
【答案】B
【解析】
.故选B.
10.(2019·新疆维吾尔自治区阿克苏市实验中学高二月考)在平行六面体ABCD-EFGH中,若=x﹣2y+3z,,则x+y+z等于( )
A. B. C. D.1
【答案】C
【解析】
在平行六面体ABCD﹣EFGH中,=++,
∵=x﹣2y+3z,=,
∴x=1,﹣2y=1,3z=1,
∴,z=,∴x+y+z=,故选:C.
二、多选题
11.(2019·山东省济南一中高二期中)已知平行六面体,则下列四式中其中正确的有( )
A. B.
C. D.
【答案】ABC
【解析】
作出平行六面体的图像如图,可得,则A正确;,则B正确;C显然正确;,则D不正确.综上,正确的有ABC.
故选:ABC
12.(2020·江苏省高二期末)如图,在正方体中,下列各式中运算的结果为的有( )
A. B.
C. D.
【答案】BCD
【解析】
A.,故错误;B.,故正确;
C.,故正确;D.,故正确.
故选:BCD.
13.(2020·山东省高二期末)已知A,B,C三点不共线,O为平面ABC外的任一点,则“点M与点A,B,C共面”的充分条件的是( )
A. B.
C. D.
【答案】BD
【解析】
当时,可知点与点共面,所以,
所以,
所以,
不妨令,,,且此时,
因为,,,,
由上可知:BD满足要求.
故选:BD.
点睛:常见的证明空间中四点共面的方法有:(1)证明;(2)对于空间中任意一点,证明;(3) 对于空间中任意一点,证明.
三、填空题
14.(2019·江苏省高二期末)直三棱柱中,若,则__________.
【答案】
【解析】
直三棱柱中,若
故答案为
15.(2019·新疆维吾尔自治区阿克苏市实验中学高二月考)已知非零向量,,且=+,+,,则中一定共线的三点是________.
【答案】A,B,D
【解析】
由向量的加法原理:.
又共点B,故A,B,D三点共线.
故答案为:A,B,D
16.(2019·浙江省诸暨中学高二期中)已知三棱锥O-ABC,点D是BC中点,P是AD中点,设,则________;x=________.
【答案】1 ;
【解析】
如图,
,
所以,所以,.
故答案为:1;
17.(2019·江苏省高二期中)如图在正方体中,已知,,,为底面的的中心,为的重心,则______
【答案】
【解析】
在正方体中,,,,
为底面的的中心,为△的重心,
.
故答案为:.
四、解答题
18.(2018·全国高二课时练习)如图,在长方体ABCD-A1B1C1D1中,AB=3,AD=2,AA1=1,以长方体的八个顶点中的两点为起点和终点的向量中.
(1)单位向量共有多少个
(2)试写出模为的所有向量.
(3)试写出与相等的所有向量.
(4)试写出的相反向量.
【答案】(1)答案见解析;(2)答案见解析;(3)答案见解析;(4)答案见解析.
【解析】
分析:
(1)根据定义模为1的向量即为单位向量(2)在长方体中求出对角线长为,即可写出所求向量(3)根据大小相等,方向相同即为相等向量可写出(4)大小相等,方向相反的向量即为相反向量.
详解:
(1)模为1的向量有,共8个单位向量.
(2)由于这个长方体的左右两侧的对角线长均为,因此模为的向量为
.
(3)与向量相等的向量(除它自身之外)为.
(4)向量的相反向量为.
19.(2020·全国高一课时练习)如图,已知一点O到平行四边形的三个顶点A,B,C的向量分别为,求.
【答案】
【解析】
因为,,所以.
20.(2019·三亚华侨学校高二期中)如图,在平行六面体中,两两夹角为60°,长度分别为2,3,1,点P在线段BC上,且,记.
(1)试用表示;
(2)求模.
【答案】(1); (2).
【解析】
(1).
(2)因为AB,AD,两两夹角为60°,长度分别为2,3,1.
所以,
.
21.(2018·全国高二课时练习)在四棱锥P-ABCD中,ABCD为平行四边形,AC与BD交于O,G为BD上一点,BG=2GD,=,= ,= ,试用基底{,,}表示向量.
【答案】
【解析】
因为BG=2GD,所以.
又=a+c-2b,
所以=b+(a+c-2b)=a-b+c.
22.(2019·全国高一课时练习)设e1,e2是不共线的空间向量,已知=2e1+ke2,=e1+3e2,=2e1-e2.若A,B,D三点共线,求k的值.
【答案】k=-8.
【解析】
分析:A,B,D三点共线,故存在唯一实数,使得,再由已知条件表示出与,建立方程组可求出和值
详解:
由已知,有-=(2e1-e2)-(e1+3e2)=e1-4e2.
∵A,B,D三点共线,∴存在实数λ,使=λ,即2e1+ke2=λ(e1-4e2),∴2e1+ke2=λe1-4λe2.
∵e1,e2是不共线的空间向量,∴,解得.
23.(2018·全国高二课时练习)已知{e1,e2,e3}是空间的一个基底,且=e1+2e2-e3,=-3e1+e2+2e3,=e1+e2-e3,试判断{}能否作为空间的一个基底 若能,试以此基底表示向量=2e1-e2+3e3;若不能,请说明理由.
【答案】能,=17-5-30.
【解析】
能作为空间的一组基底.
假设共面,由向量共面的充要条件知存在实数x,y使=x+y成立
又因为是空间的一个基底,
所以不共面.
因此此方程组无解,
即不存在实数x,y使=x+y,
所以不共面.
故{}能作为空间的一个基底.
设=p+q+z,
则有
因为为空间的一个基底,
所以解得
故=17-5-30.
点睛:如果三个向量不共面,那么对于空间任意一个向量,存在一个唯一的有序实数组使.我们把叫做空间的一个基底,其中叫基向量.
一、单选题
1.(2019·全国高二课时练习)已知,,是不共面的三个向量,则能构成一个基底的一组向量是( )
A.2,﹣,+2 B.2,﹣,+2
C.,2,﹣ D.,+,﹣
2.(2020·贵州省铜仁第一中学高二开学考试)如图所示,在平行六面体中,设,,,是的中点,试用,,表示( )
A. B. C. D.
3.(2020·山东省章丘四中高二月考)如图,在四面体中,是的中点,是的中点,则等于( )
A. B.
C. D.
4.(2020·河南省高二期末)如图在平行六面体中,为的中点,设,,,则( )
A. B. C. D.
5.(2020·广东省红岭中学高二期末) 与共线是直线AB∥CD的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.(2020·广东省红岭中学高二期末)为空间任意一点,三点不共线,若=,则四点
A.一定不共面 B.不一定共面
C.一定共面 D.无法判断
7.(2019·随州市第一中学高二期中)空间四点共面,但任意三点不共线,若为该平面外一点且,则实数的值为( )
A. B. C. D.
8.(2020·甘肃省高二期末)如图,空间四边形OABC中,,,,且,,则等于( )
A. B.
C. D.
9.(2020·广西壮族自治区高二期末)在平行六面体中,为与的交点.若,,,则下列向量中与相等的向量是( ).
A. B. C. D.
10.(2019·新疆维吾尔自治区阿克苏市实验中学高二月考)在平行六面体ABCD-EFGH中,若=x﹣2y+3z,,则x+y+z等于( )
A. B. C. D.1
二、多选题
11.(2019·山东省济南一中高二期中)已知平行六面体,则下列四式中其中正确的有( )
A. B.
C. D.
12.(2020·江苏省高二期末)如图,在正方体中,下列各式中运算的结果为的有( )
A. B.
C. D.
13.(2020·山东省高二期末)已知A,B,C三点不共线,O为平面ABC外的任一点,则“点M与点A,B,C共面”的充分条件的是( )
A. B.
C. D.
三、填空题
14.(2019·江苏省高二期末)直三棱柱中,若,则__________.
15.(2019·新疆维吾尔自治区阿克苏市实验中学高二月考)已知非零向量,,且=+,+,,则中一定共线的三点是________.
16.(2019·浙江省诸暨中学高二期中)已知三棱锥O-ABC,点D是BC中点,P是AD中点,设,则________;x=________.
17.(2019·江苏省高二期中)如图在正方体中,已知,,,为底面的的中心,为的重心,则______
四、解答题
18.(2018·全国高二课时练习)如图,在长方体ABCD-A1B1C1D1中,AB=3,AD=2,AA1=1,以长方体的八个顶点中的两点为起点和终点的向量中.
(1)单位向量共有多少个
(2)试写出模为的所有向量.
(3)试写出与相等的所有向量.
(4)试写出的相反向量.
19.(2020·全国高一课时练习)如图,已知一点O到平行四边形的三个顶点A,B,C的向量分别为,求.
20.(2019·三亚华侨学校高二期中)如图,在平行六面体中,两两夹角为60°,长度分别为2,3,1,点P在线段BC上,且,记.
(1)试用表示;
(2)求模.
21.(2018·全国高二课时练习)在四棱锥P-ABCD中,ABCD为平行四边形,AC与BD交于O,G为BD上一点,BG=2GD,=,= ,= ,试用基底{,,}表示向量.
22.(2019·全国高一课时练习)设e1,e2是不共线的空间向量,已知=2e1+ke2,=e1+3e2,=2e1-e2.若A,B,D三点共线,求k的值.
23.(2018·全国高二课时练习)已知{e1,e2,e3}是空间的一个基底,=e1+2e2-e3,=-3e1+e2+2e3,=e1+e2-e3,试判断{}能否作为空间的一个基底 若能,试以此基底表示向量=2e1-e2+3e3;若不能,请说明理由.
空间向量及其运算、空间向量基本定理答案
一、单选题
1.(2019·全国高二课时练习)已知,,是不共面的三个向量,则能构成一个基底的一组向量是( )
A.2,﹣,+2 B.2,﹣,+2
C.,2,﹣ D.,+,﹣
【答案】C
【解析】
对于A,因为2=(﹣)+(+2),得2、﹣、+2三个向量共面,故它们不能构成一个基底,A不正确;
对于B,因为2=(﹣)+(+2),得2、﹣、+2三个向量共面,故它们不能构成一个基底,B不正确;
对于C,因为找不到实数λ、μ,使=λ 2+μ(﹣)成立,故、2、﹣三个向量不共面,
它们能构成一个基底,C正确;
对于D,因为=(+)﹣(﹣),得、+、﹣三个向量共面,故它们不能构成一个基底,D不正确
故选:C.
2.(2020·贵州省铜仁第一中学高二开学考试)如图所示,在平行六面体中,设,,,是的中点,试用,,表示( )
A. B. C. D.
【答案】A
【解析】
是的中点,
.
故选:A.
3.(2020·山东省章丘四中高二月考)如图,在四面体中,是的中点,是的中点,则等于( )
A. B.
C. D.
【答案】C
【解析】
在四面体中,是的中点,是的中点
故选:C.
4.(2020·河南省高二期末)如图在平行六面体中,为的中点,设,,,则( )
A. B. C. D.
【答案】A
【解析】
由题意结合平行六面体的性质可得
.
故选:A.
5.(2020·广东省红岭中学高二期末) 与共线是直线AB∥CD的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】B
【解析】
根据向量共线的定义,可知若与共线,则它们所在的直线可能平行,也可能重合;若AB∥CD,则与共线;根据充分条件和必要条件的概念,可知与共线是直线AB∥CD的必要不充分条件,
故选B
点睛:向量共线的定义:如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量 .
6.(2020·广东省红岭中学高二期末)为空间任意一点,三点不共线,若=,则四点
A.一定不共面 B.不一定共面
C.一定共面 D.无法判断
【答案】C
【解析】:点P在平面ABC内,O是平面ABC外的任意一点,则且.利用此推论可直接证明一定共面.
详解:因为=,且,所以四点共面.
7.(2019·随州市第一中学高二期中)空间四点共面,但任意三点不共线,若为该平面外一点且,则实数的值为( )
A. B. C. D.
【答案】A
【解析】因为空间四点共面,但任意三点不共线,对于该平面外一点都有,所以,解得.故选A
8.(2020·甘肃省高二期末)如图,空间四边形OABC中,,,,且,,则等于( )
A. B.
C. D.
【答案】C
【解析】
,,,,
,故选:C.
9.(2020·广西壮族自治区高二期末)在平行六面体中,为与的交点.若,,,则下列向量中与相等的向量是( ).
A. B. C. D.
【答案】B
【解析】
.故选B.
10.(2019·新疆维吾尔自治区阿克苏市实验中学高二月考)在平行六面体ABCD-EFGH中,若=x﹣2y+3z,,则x+y+z等于( )
A. B. C. D.1
【答案】C
【解析】
在平行六面体ABCD﹣EFGH中,=++,
∵=x﹣2y+3z,=,
∴x=1,﹣2y=1,3z=1,
∴,z=,∴x+y+z=,故选:C.
二、多选题
11.(2019·山东省济南一中高二期中)已知平行六面体,则下列四式中其中正确的有( )
A. B.
C. D.
【答案】ABC
【解析】
作出平行六面体的图像如图,可得,则A正确;,则B正确;C显然正确;,则D不正确.综上,正确的有ABC.
故选:ABC
12.(2020·江苏省高二期末)如图,在正方体中,下列各式中运算的结果为的有( )
A. B.
C. D.
【答案】BCD
【解析】
A.,故错误;B.,故正确;
C.,故正确;D.,故正确.
故选:BCD.
13.(2020·山东省高二期末)已知A,B,C三点不共线,O为平面ABC外的任一点,则“点M与点A,B,C共面”的充分条件的是( )
A. B.
C. D.
【答案】BD
【解析】
当时,可知点与点共面,所以,
所以,
所以,
不妨令,,,且此时,
因为,,,,
由上可知:BD满足要求.
故选:BD.
点睛:常见的证明空间中四点共面的方法有:(1)证明;(2)对于空间中任意一点,证明;(3) 对于空间中任意一点,证明.
三、填空题
14.(2019·江苏省高二期末)直三棱柱中,若,则__________.
【答案】
【解析】
直三棱柱中,若
故答案为
15.(2019·新疆维吾尔自治区阿克苏市实验中学高二月考)已知非零向量,,且=+,+,,则中一定共线的三点是________.
【答案】A,B,D
【解析】
由向量的加法原理:.
又共点B,故A,B,D三点共线.
故答案为:A,B,D
16.(2019·浙江省诸暨中学高二期中)已知三棱锥O-ABC,点D是BC中点,P是AD中点,设,则________;x=________.
【答案】1 ;
【解析】
如图,
,
所以,所以,.
故答案为:1;
17.(2019·江苏省高二期中)如图在正方体中,已知,,,为底面的的中心,为的重心,则______
【答案】
【解析】
在正方体中,,,,
为底面的的中心,为△的重心,
.
故答案为:.
四、解答题
18.(2018·全国高二课时练习)如图,在长方体ABCD-A1B1C1D1中,AB=3,AD=2,AA1=1,以长方体的八个顶点中的两点为起点和终点的向量中.
(1)单位向量共有多少个
(2)试写出模为的所有向量.
(3)试写出与相等的所有向量.
(4)试写出的相反向量.
【答案】(1)答案见解析;(2)答案见解析;(3)答案见解析;(4)答案见解析.
【解析】
分析:
(1)根据定义模为1的向量即为单位向量(2)在长方体中求出对角线长为,即可写出所求向量(3)根据大小相等,方向相同即为相等向量可写出(4)大小相等,方向相反的向量即为相反向量.
详解:
(1)模为1的向量有,共8个单位向量.
(2)由于这个长方体的左右两侧的对角线长均为,因此模为的向量为
.
(3)与向量相等的向量(除它自身之外)为.
(4)向量的相反向量为.
19.(2020·全国高一课时练习)如图,已知一点O到平行四边形的三个顶点A,B,C的向量分别为,求.
【答案】
【解析】
因为,,所以.
20.(2019·三亚华侨学校高二期中)如图,在平行六面体中,两两夹角为60°,长度分别为2,3,1,点P在线段BC上,且,记.
(1)试用表示;
(2)求模.
【答案】(1); (2).
【解析】
(1).
(2)因为AB,AD,两两夹角为60°,长度分别为2,3,1.
所以,
.
21.(2018·全国高二课时练习)在四棱锥P-ABCD中,ABCD为平行四边形,AC与BD交于O,G为BD上一点,BG=2GD,=,= ,= ,试用基底{,,}表示向量.
【答案】
【解析】
因为BG=2GD,所以.
又=a+c-2b,
所以=b+(a+c-2b)=a-b+c.
22.(2019·全国高一课时练习)设e1,e2是不共线的空间向量,已知=2e1+ke2,=e1+3e2,=2e1-e2.若A,B,D三点共线,求k的值.
【答案】k=-8.
【解析】
分析:A,B,D三点共线,故存在唯一实数,使得,再由已知条件表示出与,建立方程组可求出和值
详解:
由已知,有-=(2e1-e2)-(e1+3e2)=e1-4e2.
∵A,B,D三点共线,∴存在实数λ,使=λ,即2e1+ke2=λ(e1-4e2),∴2e1+ke2=λe1-4λe2.
∵e1,e2是不共线的空间向量,∴,解得.
23.(2018·全国高二课时练习)已知{e1,e2,e3}是空间的一个基底,且=e1+2e2-e3,=-3e1+e2+2e3,=e1+e2-e3,试判断{}能否作为空间的一个基底 若能,试以此基底表示向量=2e1-e2+3e3;若不能,请说明理由.
【答案】能,=17-5-30.
【解析】
能作为空间的一组基底.
假设共面,由向量共面的充要条件知存在实数x,y使=x+y成立
又因为是空间的一个基底,
所以不共面.
因此此方程组无解,
即不存在实数x,y使=x+y,
所以不共面.
故{}能作为空间的一个基底.
设=p+q+z,
则有
因为为空间的一个基底,
所以解得
故=17-5-30.
点睛:如果三个向量不共面,那么对于空间任意一个向量,存在一个唯一的有序实数组使.我们把叫做空间的一个基底,其中叫基向量.
