22.3实际问题与二次函数 第2课时 生活中的抛物线 课件(25张PPT)
文档属性
| 名称 | 22.3实际问题与二次函数 第2课时 生活中的抛物线 课件(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 16:25:14 | ||
图片预览






文档简介
(共25张PPT)
第二十二章 二次函数
22.3 实际应用与二次函数
第2课时 生活中的抛物线
学习目标
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.(重点)
2.利用二次函数解决拱桥及运动中的有关问题.(重、难点)
3.能运用二次函数的图象与性质进行决策.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
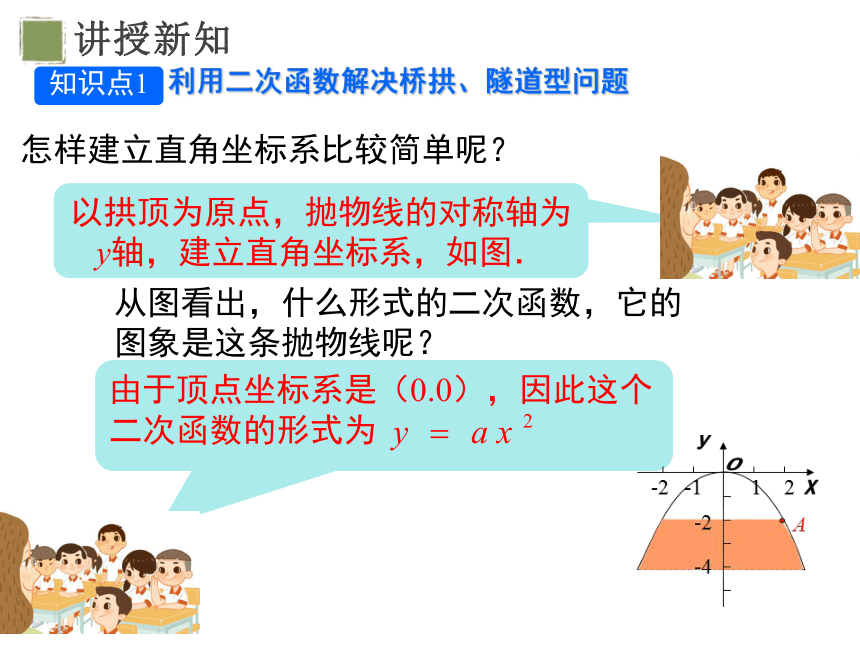
如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9米,水面宽是4米时,拱顶离水面2米.现在想了解水面宽度变化时,拱顶离水面的高度怎样变化.你能想出办法来吗?
问题
新课导入
讲授新知
贰
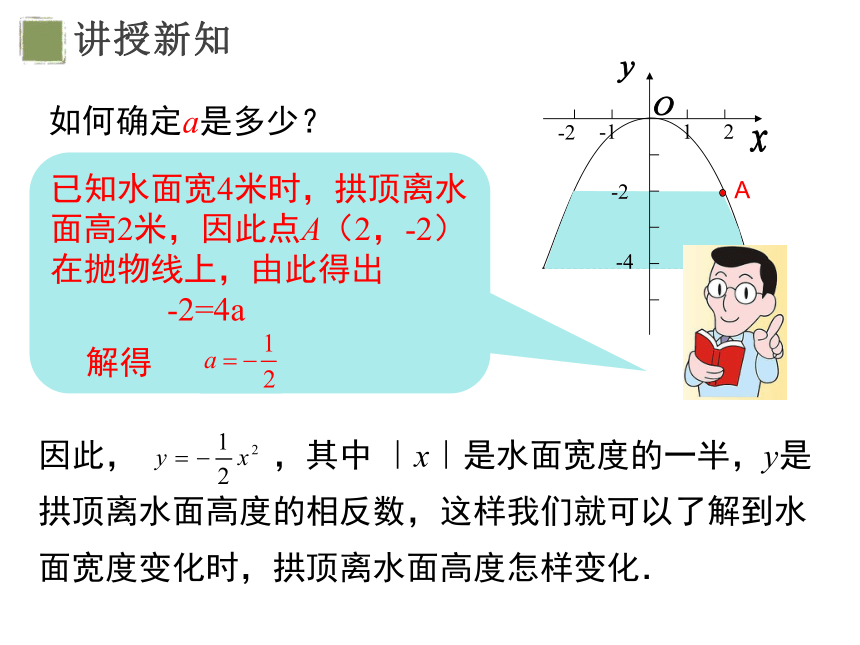
怎样建立直角坐标系比较简单呢?
以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系,如图.
从图看出,什么形式的二次函数,它的图象是这条抛物线呢?
由于顶点坐标系是(0.0),因此这个二次函数的形式为
讲授新知
利用二次函数解决桥拱、隧道型问题
知识点1
x
O
y
-2
-4
2
1
-2
-1
A
如何确定a是多少?
已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上,由此得出
-2=4a
因此, ,其中 |x|是水面宽度的一半,y是拱顶离水面高度的相反数,这样我们就可以了解到水面宽度变化时,拱顶离水面高度怎样变化.
解得
讲授新知
由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
水面宽3m时 从而
因此拱顶离水面高1.125m
现在你能求出水面宽3米时,拱顶离水面高多少米吗?
讲授新知
(1)根据题意建立适当的直角坐标系;
(2)把已知条件转化为点的坐标;
(3)合理设出函数解析式;
(4)利用待定系数法求出函数解析式;
(5)根据求得的解析式进一步分析、判断并进行有关的计算.
知识点2
利用二次函数解决运动中抛物线型问题
讲授新知
例2 在篮球赛中,姚小鸣跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米,他能把球投中吗?
3米
4米
4米
x
y
O
范例应用
3米
4米
4米
x
y
A
B
C
解:如图建立直角坐标系.则点A的坐标是(0, ),B点坐标是(4,4),C点坐标是(8,3).
因此可设抛物线的解析式是y=a(x-4)2+4 ①.
把点A(0, )代入①得
解得
所以抛物线的解析式是 .
当x=8时,则
所以此球不能投中.
判断此球能否准确投中的问题就是判断代表篮圈的点是否在抛物线上;
O
范例应用
若假设出手的角度和力度都不变,则如何才能使此球命中
(1)跳得高一点儿;
(2)向前平移一点儿.
3米
8米
4米
4米
x
y
O
范例应用
y
x
(8,3)
(4,4)
O 1 2 3 4 5 6 7 8 9 10
6
4
2
(1)跳得高一点儿;
范例应用
y
(8,3)
(4,4)
O 1 2 3 4 5 6 7 8 9 10
6
4
2
(7,3)
●
(2)向前平移一点儿.
x
范例应用
当堂训练
叁
1.足球被从地面上踢起,它距地面的高度h(m)可用公式h=
-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在 s后落地.
4
2.如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为 ,那么铅球运动过程中最高点离地面的距离为 米.
x
y
O
2
当堂训练
3.公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O点恰在水面中心,OA=1.25米,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下.为使水流较为漂亮,要求设计成水流在离OA距离为1米处达到距水面最大高度2.25米.如果不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流落不到池外?
O
A
1.25米
当堂训练
O
B
C
A
解:如图建立坐标系,设抛物线顶点
为B,水流落水与x轴交于C点.
由题意可知A( 0,1.25)、
B( 1,2.25 )、C(x0,0).
x
y
设抛物线为y=a(x-1)2+2.25 (a≠0),
点A坐标代入,得a= - 1;
当y= 0时, x1= - 0.5(舍去), x2=2.5
∴水池的半径至少要2.5米.
∴抛物线为y=-(x-1)2+2.25.
1.25
当堂训练
课堂小结
肆
转化
回归
(二次函数的图象和性质)
拱桥问题
运动中的抛物线问题
(实物中的抛物线形问题)
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
实际问题
数学模型
转化的关键
课堂小结
课后作业
基础题:1.课后整理今天所讲的两个例题.
提高题:2.请学有余力的同学做一下两类问题各两个。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第二十二章 二次函数
22.3 实际应用与二次函数
第2课时 生活中的抛物线
学习目标
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.(重点)
2.利用二次函数解决拱桥及运动中的有关问题.(重、难点)
3.能运用二次函数的图象与性质进行决策.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9米,水面宽是4米时,拱顶离水面2米.现在想了解水面宽度变化时,拱顶离水面的高度怎样变化.你能想出办法来吗?
问题
新课导入
讲授新知
贰
怎样建立直角坐标系比较简单呢?
以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系,如图.
从图看出,什么形式的二次函数,它的图象是这条抛物线呢?
由于顶点坐标系是(0.0),因此这个二次函数的形式为
讲授新知
利用二次函数解决桥拱、隧道型问题
知识点1
x
O
y
-2
-4
2
1
-2
-1
A
如何确定a是多少?
已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上,由此得出
-2=4a
因此, ,其中 |x|是水面宽度的一半,y是拱顶离水面高度的相反数,这样我们就可以了解到水面宽度变化时,拱顶离水面高度怎样变化.
解得
讲授新知
由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
水面宽3m时 从而
因此拱顶离水面高1.125m
现在你能求出水面宽3米时,拱顶离水面高多少米吗?
讲授新知
(1)根据题意建立适当的直角坐标系;
(2)把已知条件转化为点的坐标;
(3)合理设出函数解析式;
(4)利用待定系数法求出函数解析式;
(5)根据求得的解析式进一步分析、判断并进行有关的计算.
知识点2
利用二次函数解决运动中抛物线型问题
讲授新知
例2 在篮球赛中,姚小鸣跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米,他能把球投中吗?
3米
4米
4米
x
y
O
范例应用
3米
4米
4米
x
y
A
B
C
解:如图建立直角坐标系.则点A的坐标是(0, ),B点坐标是(4,4),C点坐标是(8,3).
因此可设抛物线的解析式是y=a(x-4)2+4 ①.
把点A(0, )代入①得
解得
所以抛物线的解析式是 .
当x=8时,则
所以此球不能投中.
判断此球能否准确投中的问题就是判断代表篮圈的点是否在抛物线上;
O
范例应用
若假设出手的角度和力度都不变,则如何才能使此球命中
(1)跳得高一点儿;
(2)向前平移一点儿.
3米
8米
4米
4米
x
y
O
范例应用
y
x
(8,3)
(4,4)
O 1 2 3 4 5 6 7 8 9 10
6
4
2
(1)跳得高一点儿;
范例应用
y
(8,3)
(4,4)
O 1 2 3 4 5 6 7 8 9 10
6
4
2
(7,3)
●
(2)向前平移一点儿.
x
范例应用
当堂训练
叁
1.足球被从地面上踢起,它距地面的高度h(m)可用公式h=
-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在 s后落地.
4
2.如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为 ,那么铅球运动过程中最高点离地面的距离为 米.
x
y
O
2
当堂训练
3.公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O点恰在水面中心,OA=1.25米,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下.为使水流较为漂亮,要求设计成水流在离OA距离为1米处达到距水面最大高度2.25米.如果不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流落不到池外?
O
A
1.25米
当堂训练
O
B
C
A
解:如图建立坐标系,设抛物线顶点
为B,水流落水与x轴交于C点.
由题意可知A( 0,1.25)、
B( 1,2.25 )、C(x0,0).
x
y
设抛物线为y=a(x-1)2+2.25 (a≠0),
点A坐标代入,得a= - 1;
当y= 0时, x1= - 0.5(舍去), x2=2.5
∴水池的半径至少要2.5米.
∴抛物线为y=-(x-1)2+2.25.
1.25
当堂训练
课堂小结
肆
转化
回归
(二次函数的图象和性质)
拱桥问题
运动中的抛物线问题
(实物中的抛物线形问题)
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
实际问题
数学模型
转化的关键
课堂小结
课后作业
基础题:1.课后整理今天所讲的两个例题.
提高题:2.请学有余力的同学做一下两类问题各两个。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
