人教A版(2019)高中数学选择性必修第一册课时作业:1.2空间向量基本定理(含解析)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册课时作业:1.2空间向量基本定理(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 553.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 22:19:34 | ||
图片预览


文档简介
1.2空间向量基本定理
1.已知是不共面的三个向量,则能构成空间的一个基底的一组向量是( )
A. B.
C. D.
2.已知是三个非零向量;为空间的一个基底,则是的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
3.在以下三个命题中,真命题的个数是( )
①若三个非零向量不能构成空间的一个基底,则共面;②若两个非零向量与任何一个向量都不能构成空间的一个基底,则共线;③若是两个不共线的向量,而(且),则构成空间的一个基底.
A.0 B.1 C.2 D.3
4.在空间四点中,若是空间的一个基底,则下列命题不正确的是( )
A.四点不共线 B.四点共面,但不共线
C.四点不共面 D.四点中任意三点不共线
5.已知四面体是的重心,是上点,且,若,则为( )
A. B. C. D.
6.已知四点互不重合且任意三点不共线,则下列式子中能使成为空间的一个基底的是( )
A. B.
C. D.
7.已知为空间的一个基底,若,,且,则分别为( )
A. B. C. D.
8.在正方体中,分别是的中点,以为基底,,则的值是( )
A. B.
C. D.
9.已知为空间不共面的四点,且向量,向量,则与不能构成空间基底的是( )
A. B. C. D.或
10.如图,在四面体中,为的重心,是上一点,,以为基底,则___________.
11.已知是空间五点,且任何三点不共线.若与均不能构成空间的一个基底,则下列结论:
①不能构成空间的一个基底;②不能构成空间的一个基底;③不能构成空间的一个基地;④能构成空间的一个基底.
其中正确的有_________个.
12.在平面六面体中,若,则_______.
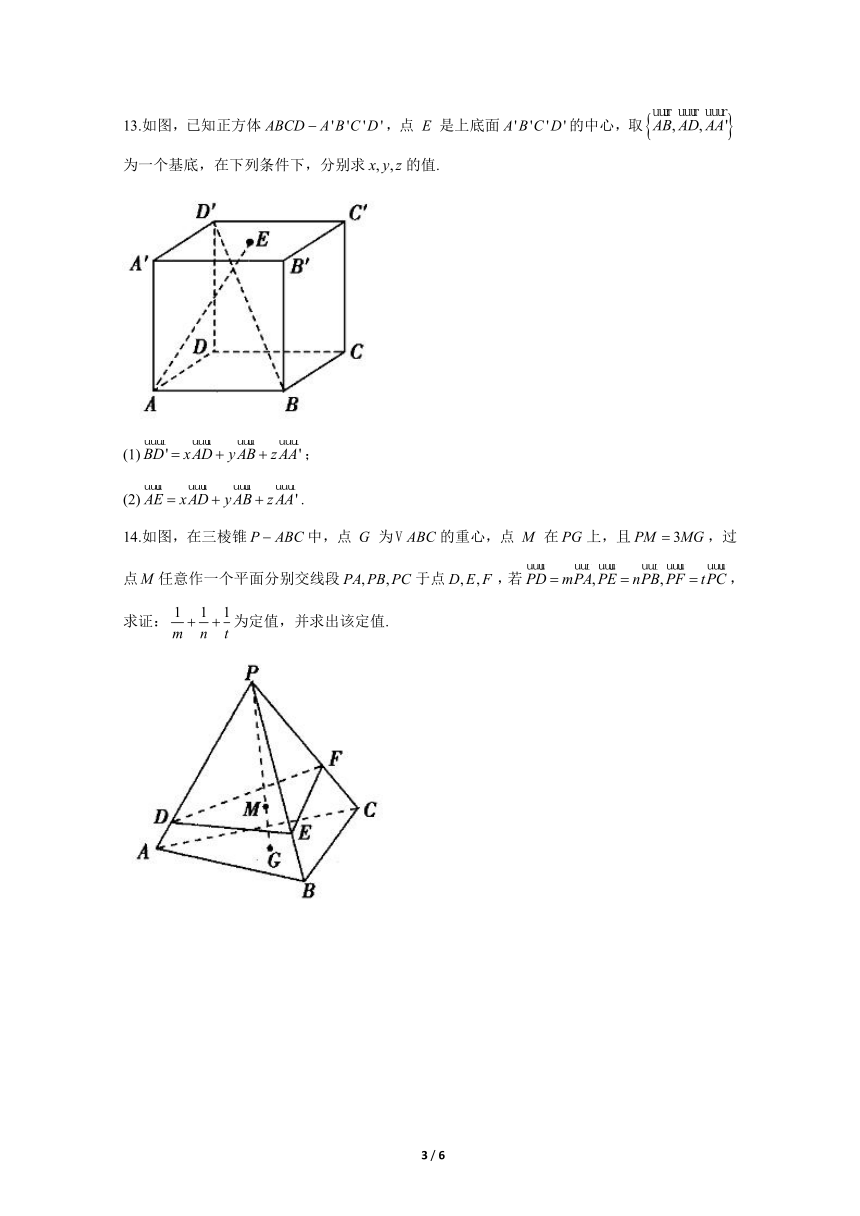
13.如图,已知正方体,点是上底面的中心,取为一个基底,在下列条件下,分别求的值.
(1);
(2).
14.如图,在三棱锥中,点为的重心,点在上,且,过点任意作一个平面分别交线段于点,若,求证:为定值,并求出该定值.
答案以及解析
1.答案:C
解析:对于选项A,有,则共面,不能作为基底;同理可判断选项中的向量共面.故选C.
2.答案:B
解析:三个不共面的向量才能作为空间的一个基底,故不能推出,但可以推出.故选B.
3.答案:C
解析:①正确,作为基底的向量必须不共面;②正确;③错误,不共线,当时,共面,故只有①②正确.
4.答案:B
解析:选项A对应的命题是正确的,若四点共线,则相连共面,构不成基底;选项B对应的命题是错误的,若四点共面,则共面,构不成基底;选项C对应的命题是正确的,若四点共面,则构不成基底;选项D对应的命题是正确的,若有三点共线,则这四个点共面,向量构不成基底.
5.答案:A
解析:如图所示,连接并延长,交于点,则点为的中点,,.,,故选A.
6.答案:C
解析:对于选项A,由四点共面,知共面;对于选项B,D,易知共面,故选C.
7.答案:A
解析:由题意知.
又,所以,解得.
8.答案:A
解析:,对比,可得.
9.答案:C
解析:∵,∴与共面,∴不能构成空间基底.
10.答案:
解析:连接交于点,连接,则
11.答案:3
解析:由题意知空间五点共面,故①②③正确,④错误.
12.答案:
解析:∵,又,∴,即,故.
13.答案:(1)因为,又,
所以.
(2)因为
又,所以.
14.答案:连接并延长交于点,由题意,可令为空间的一个基底,
.
连接.因为点共面,所以存在实数,使得,即,
所以.
由空间向量基本定理,知,
所以,为定值.
PAGE
4 / 6
1.已知是不共面的三个向量,则能构成空间的一个基底的一组向量是( )
A. B.
C. D.
2.已知是三个非零向量;为空间的一个基底,则是的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
3.在以下三个命题中,真命题的个数是( )
①若三个非零向量不能构成空间的一个基底,则共面;②若两个非零向量与任何一个向量都不能构成空间的一个基底,则共线;③若是两个不共线的向量,而(且),则构成空间的一个基底.
A.0 B.1 C.2 D.3
4.在空间四点中,若是空间的一个基底,则下列命题不正确的是( )
A.四点不共线 B.四点共面,但不共线
C.四点不共面 D.四点中任意三点不共线
5.已知四面体是的重心,是上点,且,若,则为( )
A. B. C. D.
6.已知四点互不重合且任意三点不共线,则下列式子中能使成为空间的一个基底的是( )
A. B.
C. D.
7.已知为空间的一个基底,若,,且,则分别为( )
A. B. C. D.
8.在正方体中,分别是的中点,以为基底,,则的值是( )
A. B.
C. D.
9.已知为空间不共面的四点,且向量,向量,则与不能构成空间基底的是( )
A. B. C. D.或
10.如图,在四面体中,为的重心,是上一点,,以为基底,则___________.
11.已知是空间五点,且任何三点不共线.若与均不能构成空间的一个基底,则下列结论:
①不能构成空间的一个基底;②不能构成空间的一个基底;③不能构成空间的一个基地;④能构成空间的一个基底.
其中正确的有_________个.
12.在平面六面体中,若,则_______.
13.如图,已知正方体,点是上底面的中心,取为一个基底,在下列条件下,分别求的值.
(1);
(2).
14.如图,在三棱锥中,点为的重心,点在上,且,过点任意作一个平面分别交线段于点,若,求证:为定值,并求出该定值.
答案以及解析
1.答案:C
解析:对于选项A,有,则共面,不能作为基底;同理可判断选项中的向量共面.故选C.
2.答案:B
解析:三个不共面的向量才能作为空间的一个基底,故不能推出,但可以推出.故选B.
3.答案:C
解析:①正确,作为基底的向量必须不共面;②正确;③错误,不共线,当时,共面,故只有①②正确.
4.答案:B
解析:选项A对应的命题是正确的,若四点共线,则相连共面,构不成基底;选项B对应的命题是错误的,若四点共面,则共面,构不成基底;选项C对应的命题是正确的,若四点共面,则构不成基底;选项D对应的命题是正确的,若有三点共线,则这四个点共面,向量构不成基底.
5.答案:A
解析:如图所示,连接并延长,交于点,则点为的中点,,.,,故选A.
6.答案:C
解析:对于选项A,由四点共面,知共面;对于选项B,D,易知共面,故选C.
7.答案:A
解析:由题意知.
又,所以,解得.
8.答案:A
解析:,对比,可得.
9.答案:C
解析:∵,∴与共面,∴不能构成空间基底.
10.答案:
解析:连接交于点,连接,则
11.答案:3
解析:由题意知空间五点共面,故①②③正确,④错误.
12.答案:
解析:∵,又,∴,即,故.
13.答案:(1)因为,又,
所以.
(2)因为
又,所以.
14.答案:连接并延长交于点,由题意,可令为空间的一个基底,
.
连接.因为点共面,所以存在实数,使得,即,
所以.
由空间向量基本定理,知,
所以,为定值.
PAGE
4 / 6
