人教版数学八年级上册第十一章 全等三角形复习 课件(共17张PPT)
文档属性
| 名称 | 人教版数学八年级上册第十一章 全等三角形复习 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 330.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 17:04:26 | ||
图片预览


文档简介
(共17张PPT)
第十二章 全等三角形
全等形
全等三角形
对应边相等,对应角相等
SSS、SAS、ASA、AAS、HL
解决问题
能完全重合的图形
能完全重合的三角形
性 质
判 定
A
B
D
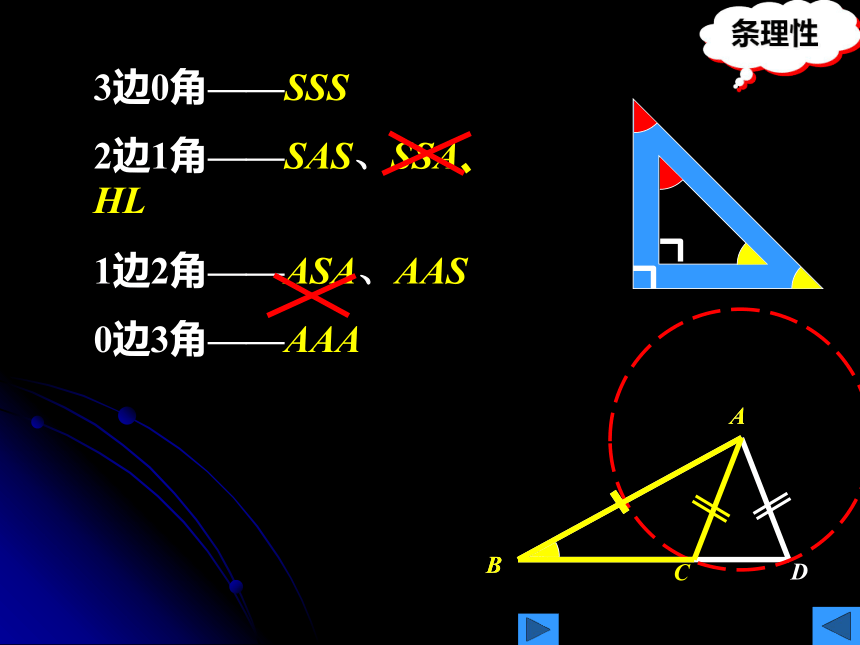
3边0角——SSS
2边1角——SAS、SSA、HL
1边2角——ASA、AAS
0边3角——AAA
条理性
C
A
B
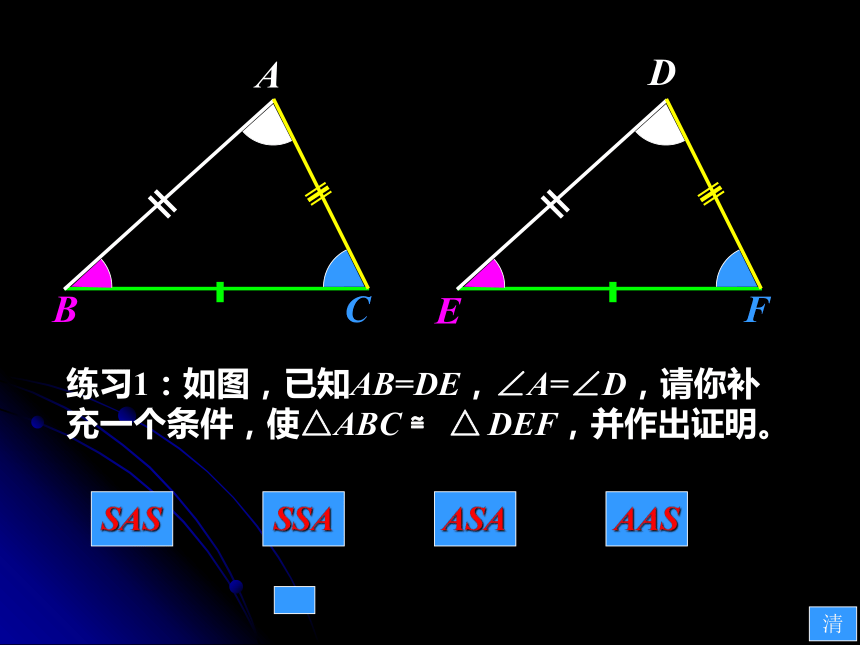
练习1:如图,已知AB=DE,∠A=∠D,请你补充一个条件,使△ABC ≌ △ DEF,并作出证明。
A
D
B
C
E
F
清
SAS
SSA
ASA
AAS
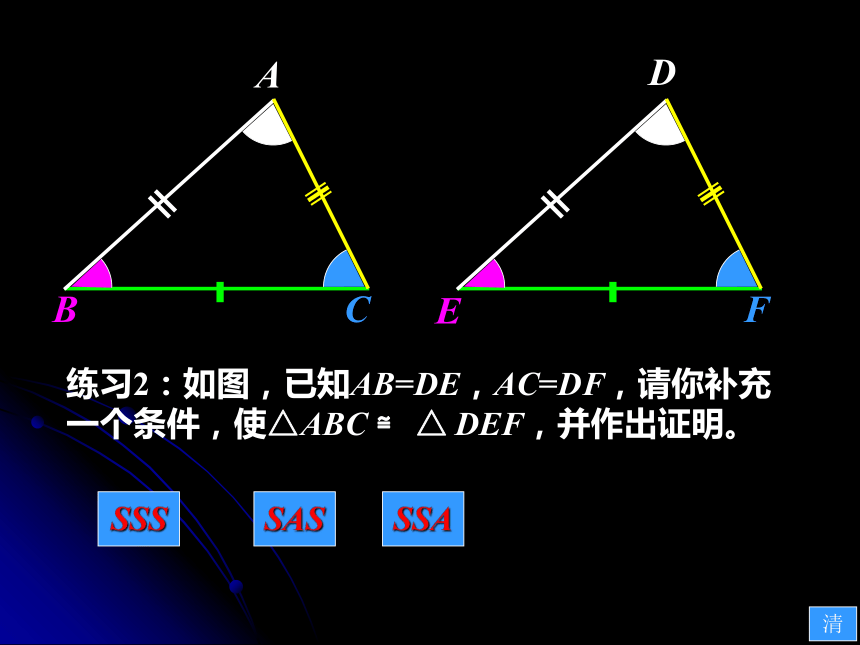
练习2:如图,已知AB=DE,AC=DF,请你补充一个条件,使△ABC ≌ △ DEF,并作出证明。
A
D
B
C
E
F
清
SSS
SAS
SSA
A
B
C
D
E
练习3:如图,已知AB=AC,AD=AE,要使△ABD≌△ACE,可以补充的条件是( )
A.∠B=∠C B.∠ADB=∠AE C
C.∠1=∠2 D.∠ADE=∠DED
2
1
清
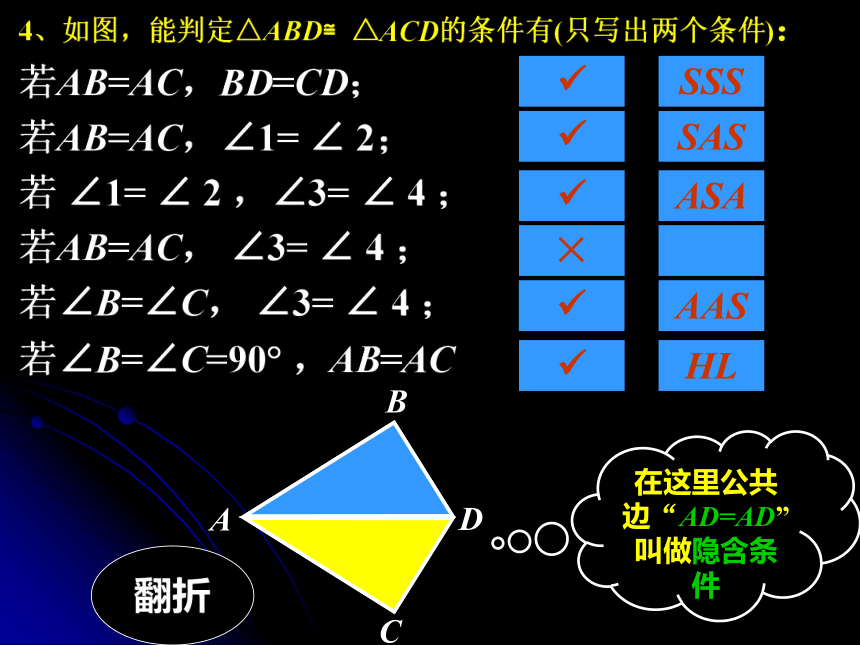
4、如图,能判定△ABD≌△ACD的条件有(只写出两个条件):
若AB=AC,BD=CD;
若AB=AC,∠1= ∠ 2;
若 ∠1= ∠ 2 ,∠3= ∠ 4 ;
若AB=AC, ∠3= ∠ 4 ;
若∠B=∠C, ∠3= ∠ 4 ;
若∠B=∠C=90 ,AB=AC
SSS
×
SAS
ASA
AAS
HL
A
B
C
D
2
1
4
3
在这里公共边“AD=AD”叫做隐含条件
翻折
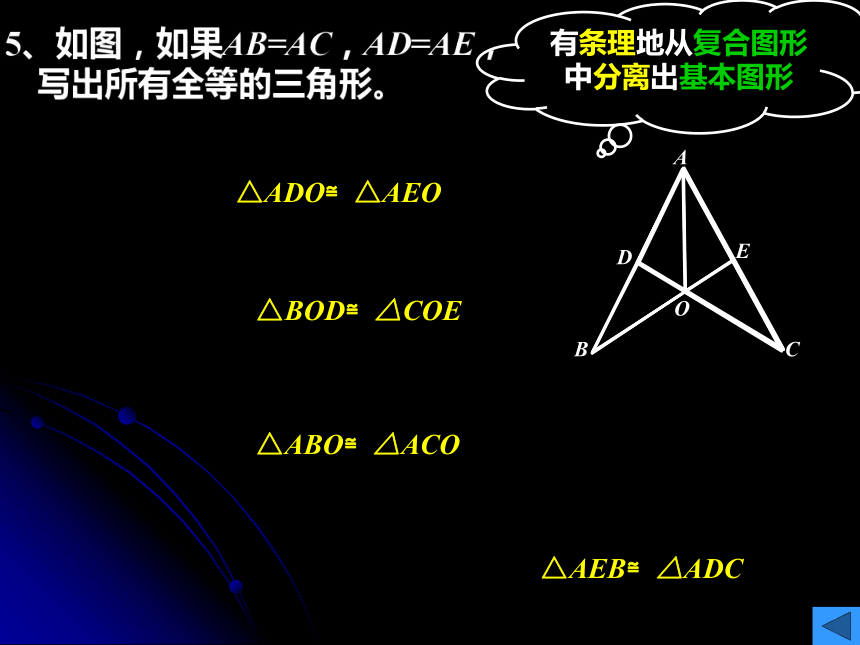
5、如图,如果AB=AC,AD=AE,写出所有全等的三角形。
A
D
E
B
C
O
△ADO≌△AEO
△BOD≌△COE
△ABO≌△ACO
△AEB≌△ADC
有条理地从复合图形中分离出基本图形
寻找三角形全等的隐含条件的方法总结
在证明三角形全等的问题中,题设往往只直接给出一个或两个条件(有时甚至连一个也没有。),其余的条件往往隐含在题设或图形之中,如何寻找这隐含的条件?现将几种常见的思路方法总结如下:
1、利用公共边相等。
2、利用公共角相等。
3、利用对顶角相等。
4、利用等边加(减)等(同)边,其和(差)相等。
5、利用等角加(减)等(同)边,其和(差)相等。
6、利用同角或等角的余(补)角相等。
7、利用垂直的定义得出直角相等。
8、利用由平行线得到的同位角、内错角相等。
A
B
C
D
E
F
6、如图,已知AB=DE,AC=DF,BE=CF。
求证:△ABC≌△DEF
证明:
∴BE+EC=CF+EC
即BC=EF
在△ABC 和△DEF中
∴△ABC≌△DEF(SSS)
在这里
“BC=EF”叫做间接条件,需要先证明;而“AB=DE”和“AC=DF”是
直接条件,不用先证明。
AB=DE
AC=DF
BE=CF
BC=EF
∵BE=CF
平移
A
B
C
D
E
F
7、如图,已知AB//DE,BC//EF,AF=CD。
求证:AB=DE
旋转
A
B
C
D
E
F
8、已知:如图,等边三角形ABC中,D、E、F分别是AB、BC、CD上的点,BE=CF=AD。
(1)求证:△ADF≌△BED≌△CFE。
(2)当点E在什么位置时,△DEF与△ADF全等,为什么?
动态几何
A
B
C
D
E
F
作业:如图,已知△ABC是等边三角形,D、E、F分别是三边上的点,且DE⊥BC,EF⊥AC,FD⊥AB。求证:△ADF≌△BED≌△CFE
全等变换
平移
旋转
翻折
(又叫轴对称变换)
全等的条件:
(1)直接条件和间接条件
(2)明显条件和隐藏条件
注意:
(1)数学中的条理性
(2)从复合图形中分离出独立图形
如图,△ABC和△ADE为等边三角形。则线段BE和CD有什么大小关系?它们的夹角为多少度?
A
B
C
D
E
如图,△ABC和△ADE为等边三角形。则线段BE和CD有什么大小关系?它们的夹角为多少度?
A
B
C
D
E
第十二章 全等三角形
全等形
全等三角形
对应边相等,对应角相等
SSS、SAS、ASA、AAS、HL
解决问题
能完全重合的图形
能完全重合的三角形
性 质
判 定
A
B
D
3边0角——SSS
2边1角——SAS、SSA、HL
1边2角——ASA、AAS
0边3角——AAA
条理性
C
A
B
练习1:如图,已知AB=DE,∠A=∠D,请你补充一个条件,使△ABC ≌ △ DEF,并作出证明。
A
D
B
C
E
F
清
SAS
SSA
ASA
AAS
练习2:如图,已知AB=DE,AC=DF,请你补充一个条件,使△ABC ≌ △ DEF,并作出证明。
A
D
B
C
E
F
清
SSS
SAS
SSA
A
B
C
D
E
练习3:如图,已知AB=AC,AD=AE,要使△ABD≌△ACE,可以补充的条件是( )
A.∠B=∠C B.∠ADB=∠AE C
C.∠1=∠2 D.∠ADE=∠DED
2
1
清
4、如图,能判定△ABD≌△ACD的条件有(只写出两个条件):
若AB=AC,BD=CD;
若AB=AC,∠1= ∠ 2;
若 ∠1= ∠ 2 ,∠3= ∠ 4 ;
若AB=AC, ∠3= ∠ 4 ;
若∠B=∠C, ∠3= ∠ 4 ;
若∠B=∠C=90 ,AB=AC
SSS
×
SAS
ASA
AAS
HL
A
B
C
D
2
1
4
3
在这里公共边“AD=AD”叫做隐含条件
翻折
5、如图,如果AB=AC,AD=AE,写出所有全等的三角形。
A
D
E
B
C
O
△ADO≌△AEO
△BOD≌△COE
△ABO≌△ACO
△AEB≌△ADC
有条理地从复合图形中分离出基本图形
寻找三角形全等的隐含条件的方法总结
在证明三角形全等的问题中,题设往往只直接给出一个或两个条件(有时甚至连一个也没有。),其余的条件往往隐含在题设或图形之中,如何寻找这隐含的条件?现将几种常见的思路方法总结如下:
1、利用公共边相等。
2、利用公共角相等。
3、利用对顶角相等。
4、利用等边加(减)等(同)边,其和(差)相等。
5、利用等角加(减)等(同)边,其和(差)相等。
6、利用同角或等角的余(补)角相等。
7、利用垂直的定义得出直角相等。
8、利用由平行线得到的同位角、内错角相等。
A
B
C
D
E
F
6、如图,已知AB=DE,AC=DF,BE=CF。
求证:△ABC≌△DEF
证明:
∴BE+EC=CF+EC
即BC=EF
在△ABC 和△DEF中
∴△ABC≌△DEF(SSS)
在这里
“BC=EF”叫做间接条件,需要先证明;而“AB=DE”和“AC=DF”是
直接条件,不用先证明。
AB=DE
AC=DF
BE=CF
BC=EF
∵BE=CF
平移
A
B
C
D
E
F
7、如图,已知AB//DE,BC//EF,AF=CD。
求证:AB=DE
旋转
A
B
C
D
E
F
8、已知:如图,等边三角形ABC中,D、E、F分别是AB、BC、CD上的点,BE=CF=AD。
(1)求证:△ADF≌△BED≌△CFE。
(2)当点E在什么位置时,△DEF与△ADF全等,为什么?
动态几何
A
B
C
D
E
F
作业:如图,已知△ABC是等边三角形,D、E、F分别是三边上的点,且DE⊥BC,EF⊥AC,FD⊥AB。求证:△ADF≌△BED≌△CFE
全等变换
平移
旋转
翻折
(又叫轴对称变换)
全等的条件:
(1)直接条件和间接条件
(2)明显条件和隐藏条件
注意:
(1)数学中的条理性
(2)从复合图形中分离出独立图形
如图,△ABC和△ADE为等边三角形。则线段BE和CD有什么大小关系?它们的夹角为多少度?
A
B
C
D
E
如图,△ABC和△ADE为等边三角形。则线段BE和CD有什么大小关系?它们的夹角为多少度?
A
B
C
D
E
