北师大版八年级上册数学 4.3.2一次函数的图像与性质 课件(共19张PPT)
文档属性
| 名称 | 北师大版八年级上册数学 4.3.2一次函数的图像与性质 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 701.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
一次函数的图象
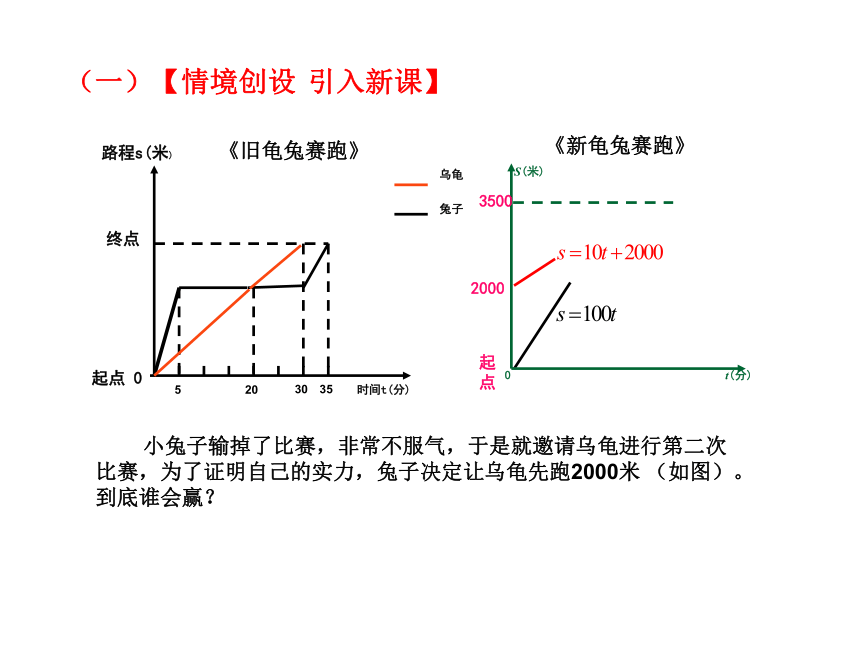
(一)【情境创设 引入新课】
小兔子输掉了比赛,非常不服气,于是就邀请乌龟进行第二次比赛,为了证明自己的实力,兔子决定让乌龟先跑2000米 (如图)。到底谁会赢?
《旧龟兔赛跑》
乌龟
兔子
时间t(分)
35
20
30
5
起点 0
终点
路程s(米)
t(分)
0
3500
S(米)
2000
起点
《新龟兔赛跑》
议一议:
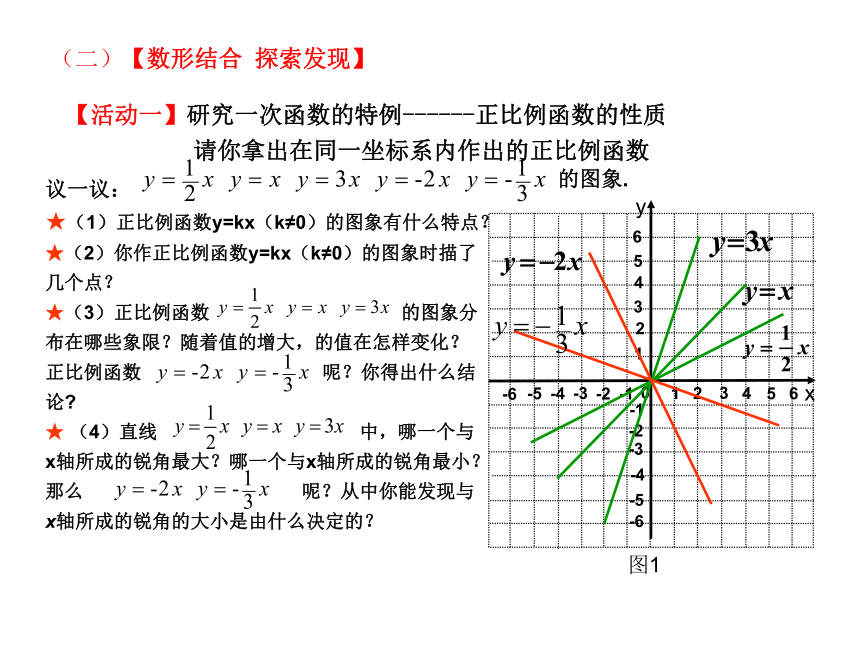
★(1)正比例函数y=kx(k≠0)的图象有什么特点?
★(2)你作正比例函数y=kx(k≠0)的图象时描了几个点?
★(3)正比例函数 的图象分布在哪些象限?随着值的增大,的值在怎样变化?正比例函数 呢?你得出什么结论
★ (4)直线 中,哪一个与x轴所成的锐角最大?哪一个与x轴所成的锐角最小?那么 呢?从中你能发现与x轴所成的锐角的大小是由什么决定的?
请你拿出在同一坐标系内作出的正比例函数
的图象.
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图1
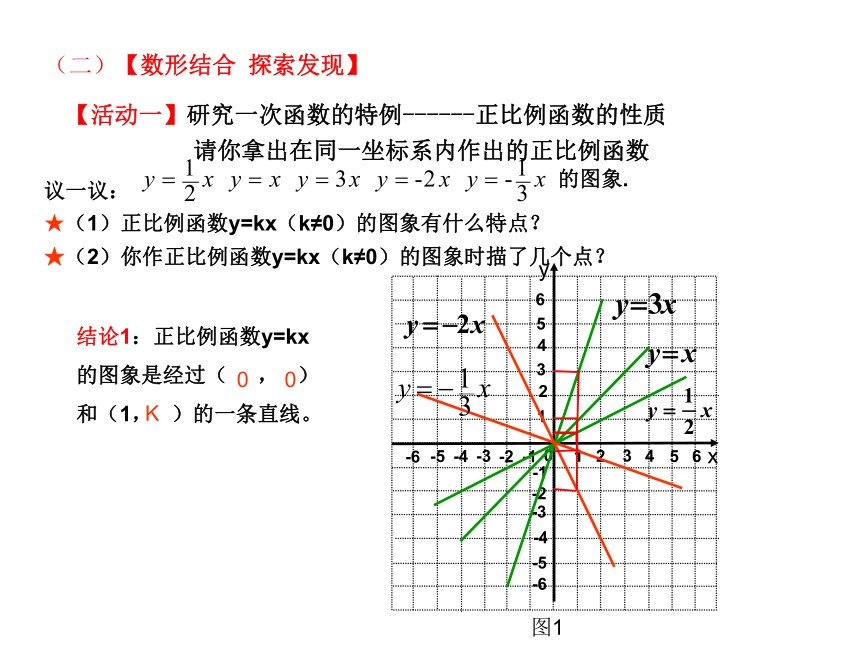
【活动一】研究一次函数的特例------正比例函数的性质
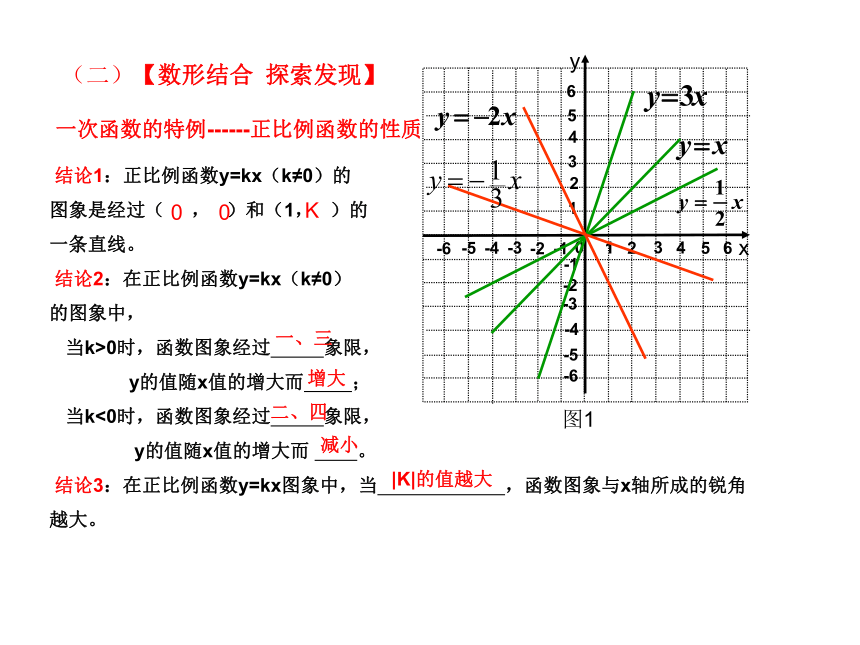
(二)【数形结合 探索发现】
议一议:
★(1)正比例函数y=kx(k≠0)的图象有什么特点?
★(2)你作正比例函数y=kx(k≠0)的图象时描了几个点?
请你拿出在同一坐标系内作出的正比例函数
的图象.
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图1
结论1:正比例函数y=kx的图象是经过( , )和(1, )的一条直线。
0 0
K
【活动一】研究一次函数的特例------正比例函数的性质
(二)【数形结合 探索发现】
议一议:
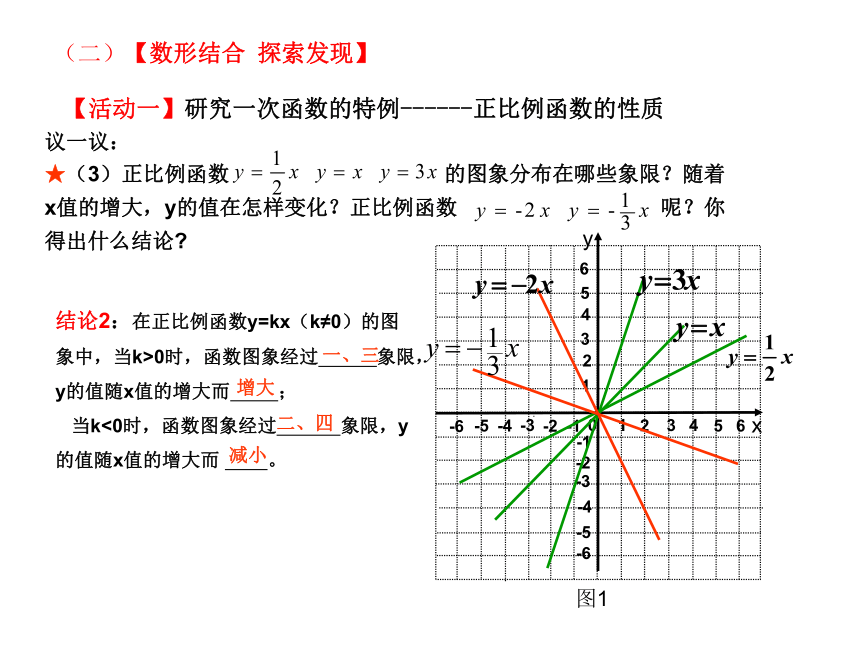
★(3)正比例函数 的图象分布在哪些象限?随着x值的增大,y的值在怎样变化?正比例函数 呢?你得出什么结论
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图1
结论2:在正比例函数y=kx(k≠0)的图象中,当k>0时,函数图象经过 象限,y的值随x值的增大而 ;
当k<0时,函数图象经过 象限,y的值随x值的增大而 。
一、三
增大
减小
二、四
【活动一】研究一次函数的特例------正比例函数的性质
(二)【数形结合 探索发现】
★ (4)直线 中,哪一个与x轴所成的锐角最大?哪一个与x轴所成的锐角最小?那么
呢?从中你能发现与x轴所成的锐角的大小是由什么决定的?
请你拿出在同一坐标系内作出的正比例函数
的图象.
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图1
【活动一】研究一次函数的特例------正比例函数的性质
结论3:在正比例函数y=kx(k≠0)图象中,当 ,函数图象与x轴所成的锐角越大。
|K|的值越大
(二)【数形结合 探索发现】
结论1:正比例函数y=kx(k≠0)的
图象是经过( , )和(1, )的
一条直线。
结论2:在正比例函数y=kx(k≠0)
的图象中,
当k>0时,函数图象经过 象限,
y的值随x值的增大而 ;
当k<0时,函数图象经过 象限,
y的值随x值的增大而 。
结论3:在正比例函数y=kx图象中,当 ,函数图象与x轴所成的锐角越大。
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图1
0 0
K
一、三
二、四
增大
减小
|K|的值越大
一次函数的特例------正比例函数的性质
(二)【数形结合 探索发现】
请你拿出在图2中做出的一次函数y=3x,y=3x+4,y=3x-6的图象
和在图3中作出的一次函数 的图象。
以及在图4中作出的一次函数y=2x+6, y= -x+6, y=5x的图象。
2、【活动二】研究一次函数的性质—— k、b对一次函数的影响。
y=3x
y=3x+4
y=3x-6
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图2
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图3
(二)【数形结合 探索发现】
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图2
★ (1)直线y=3x,y=3x+4,y=3x-6的位置关系如何?这三条直线是通过怎样
的变换而相互得到的?直线 的位置关系如何?你得出什么结论?
y=3x
y=3x+4
y=3x-6
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图3
2、【活动二】研究一次函数的性质—— k、b对一次函数的影响。
结论4:K相同,b不同的直线会平行.一次函数y=kx+b(k≠0)的图象是经过点(0,b)且平行于直线y=kx (k≠0)的一条直线。
(二)【数形结合 探索发现】
★ (2)观察图2、图3中的函数图象,它们分别分布在哪些象限?随着x值的变化,y的值在怎样变化?你得出什么结论?
2、【活动二】研究一次函数的性质—— k、b对一次函数的影响。
y=3x
y=3x+4
y=3x-6
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图2
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图3
(二)【数形结合 探索发现】
o
y
x
o
y
x
o
y
x
o
y
x
o
y
x
o
y
x
y=kx+b
(k>0 b=0)
(k<0 b=0)
(k>0 b>0)
(k>0 b<0)
(k<0 b>0)
(k<0 b<0)
y的值随x值
的增大而增大
y的值随x值
的增大而减小
经过一、三象限
经过一、二、三象限
经过一、三、四象限
经过二、四象限
经过一、二、四象限
经过二、三、四象限
归纳总结 知识升华--------- k、b对一次函数的影响。
b
b
b
b
一次函数y=kx+b(k≠0)的图象是经过点(0,b)且平行于直线y=kx (k≠0)的一条直线。
① k影响到直线的倾斜方向。|k|越大函数图象与x轴所成的锐角越大。 ② b影响直线与y轴的交点位置。直线Y=kx+b (k≠0)与y轴的交点坐标就是(0,b)③ K相同,b不同的直线会平行。
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图4
2、【活动二】研究一次函数的性质—— k、b对一次函数的影响。
★ (3)观察图4中直线Y=2x+6与y= -x+6、y=5x的位置关系如何?你得出什么结论?
★ (4)观察图4中 x从0开始逐渐增大时,y=2x+6和y=5x哪一个的值先达到20?这说明了什么
结论5: K不同,直线会相交.
y=5x
y=2x+6
y= -x+6
结论6:y=5x先到达20,这说明k值越大,y的变化量越大.
(二)【数形结合 探索发现】
3500
t(分)
S(米)
0
500
起点
1000
1500
2000
3000
60
2500
10
20
40
30
50
70
乌龟
兔子
《新龟兔赛跑》
首尾呼应 问题解决:兔子决定让乌龟先跑2000米 (如图)到底谁会赢?
(三)【师生共析 知识应用】
★1、说出下列函数图象所经过的象限,并说明?随着x值的变化,y的值在怎样变化.
(1)y=2x (2)y= -4x+3
★★★2、看图象,确定一次函数y=kx+b(k≠0) 中k,b的符号。
o
x
y
o
x
y
o
x
y
K>0 b>0
K<0 b>0
K<0 b<0
(四)【分层练习 整合提升】
★1.比一比,看谁画得快
一次函数的图象如图所示,你能画出函数 的图象吗?
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
y=x
y=x+4
y=x-5
★★2.判断下列各组直线的位置关系:
(A) 与 ;
(B) 与 .
★★3、.若一次函数y=kx+b中,
y随x的增大而减小,则( )
A.k<0,b<0 B.k<0,b>0
C.k<0,b≠0 D.k<0,b为任意数
D
思维拓展
★★★5、直线y=kx+b经过一、二、四象限,那么直线y=bx+k经过哪些象限?
o
y
x
b
K<0
o
y
x
经过一、三、四象限
K<0
经过一、二、四象限
y=bx+k
b>0
b>0
(五)【知识盛宴 星级评价】
一起来整理所学的知识吧……
本节课我一共摘取了 颗“★”,我认为我这一节课的表现(很棒、一般、 没发挥出来 、 还需努力)
我收获了……
一次函数的图象
(一)【情境创设 引入新课】
小兔子输掉了比赛,非常不服气,于是就邀请乌龟进行第二次比赛,为了证明自己的实力,兔子决定让乌龟先跑2000米 (如图)。到底谁会赢?
《旧龟兔赛跑》
乌龟
兔子
时间t(分)
35
20
30
5
起点 0
终点
路程s(米)
t(分)
0
3500
S(米)
2000
起点
《新龟兔赛跑》
议一议:
★(1)正比例函数y=kx(k≠0)的图象有什么特点?
★(2)你作正比例函数y=kx(k≠0)的图象时描了几个点?
★(3)正比例函数 的图象分布在哪些象限?随着值的增大,的值在怎样变化?正比例函数 呢?你得出什么结论
★ (4)直线 中,哪一个与x轴所成的锐角最大?哪一个与x轴所成的锐角最小?那么 呢?从中你能发现与x轴所成的锐角的大小是由什么决定的?
请你拿出在同一坐标系内作出的正比例函数
的图象.
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图1
【活动一】研究一次函数的特例------正比例函数的性质
(二)【数形结合 探索发现】
议一议:
★(1)正比例函数y=kx(k≠0)的图象有什么特点?
★(2)你作正比例函数y=kx(k≠0)的图象时描了几个点?
请你拿出在同一坐标系内作出的正比例函数
的图象.
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图1
结论1:正比例函数y=kx的图象是经过( , )和(1, )的一条直线。
0 0
K
【活动一】研究一次函数的特例------正比例函数的性质
(二)【数形结合 探索发现】
议一议:
★(3)正比例函数 的图象分布在哪些象限?随着x值的增大,y的值在怎样变化?正比例函数 呢?你得出什么结论
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图1
结论2:在正比例函数y=kx(k≠0)的图象中,当k>0时,函数图象经过 象限,y的值随x值的增大而 ;
当k<0时,函数图象经过 象限,y的值随x值的增大而 。
一、三
增大
减小
二、四
【活动一】研究一次函数的特例------正比例函数的性质
(二)【数形结合 探索发现】
★ (4)直线 中,哪一个与x轴所成的锐角最大?哪一个与x轴所成的锐角最小?那么
呢?从中你能发现与x轴所成的锐角的大小是由什么决定的?
请你拿出在同一坐标系内作出的正比例函数
的图象.
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图1
【活动一】研究一次函数的特例------正比例函数的性质
结论3:在正比例函数y=kx(k≠0)图象中,当 ,函数图象与x轴所成的锐角越大。
|K|的值越大
(二)【数形结合 探索发现】
结论1:正比例函数y=kx(k≠0)的
图象是经过( , )和(1, )的
一条直线。
结论2:在正比例函数y=kx(k≠0)
的图象中,
当k>0时,函数图象经过 象限,
y的值随x值的增大而 ;
当k<0时,函数图象经过 象限,
y的值随x值的增大而 。
结论3:在正比例函数y=kx图象中,当 ,函数图象与x轴所成的锐角越大。
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图1
0 0
K
一、三
二、四
增大
减小
|K|的值越大
一次函数的特例------正比例函数的性质
(二)【数形结合 探索发现】
请你拿出在图2中做出的一次函数y=3x,y=3x+4,y=3x-6的图象
和在图3中作出的一次函数 的图象。
以及在图4中作出的一次函数y=2x+6, y= -x+6, y=5x的图象。
2、【活动二】研究一次函数的性质—— k、b对一次函数的影响。
y=3x
y=3x+4
y=3x-6
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图2
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图3
(二)【数形结合 探索发现】
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图2
★ (1)直线y=3x,y=3x+4,y=3x-6的位置关系如何?这三条直线是通过怎样
的变换而相互得到的?直线 的位置关系如何?你得出什么结论?
y=3x
y=3x+4
y=3x-6
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图3
2、【活动二】研究一次函数的性质—— k、b对一次函数的影响。
结论4:K相同,b不同的直线会平行.一次函数y=kx+b(k≠0)的图象是经过点(0,b)且平行于直线y=kx (k≠0)的一条直线。
(二)【数形结合 探索发现】
★ (2)观察图2、图3中的函数图象,它们分别分布在哪些象限?随着x值的变化,y的值在怎样变化?你得出什么结论?
2、【活动二】研究一次函数的性质—— k、b对一次函数的影响。
y=3x
y=3x+4
y=3x-6
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图2
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图3
(二)【数形结合 探索发现】
o
y
x
o
y
x
o
y
x
o
y
x
o
y
x
o
y
x
y=kx+b
(k>0 b=0)
(k<0 b=0)
(k>0 b>0)
(k>0 b<0)
(k<0 b>0)
(k<0 b<0)
y的值随x值
的增大而增大
y的值随x值
的增大而减小
经过一、三象限
经过一、二、三象限
经过一、三、四象限
经过二、四象限
经过一、二、四象限
经过二、三、四象限
归纳总结 知识升华--------- k、b对一次函数的影响。
b
b
b
b
一次函数y=kx+b(k≠0)的图象是经过点(0,b)且平行于直线y=kx (k≠0)的一条直线。
① k影响到直线的倾斜方向。|k|越大函数图象与x轴所成的锐角越大。 ② b影响直线与y轴的交点位置。直线Y=kx+b (k≠0)与y轴的交点坐标就是(0,b)③ K相同,b不同的直线会平行。
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
图4
2、【活动二】研究一次函数的性质—— k、b对一次函数的影响。
★ (3)观察图4中直线Y=2x+6与y= -x+6、y=5x的位置关系如何?你得出什么结论?
★ (4)观察图4中 x从0开始逐渐增大时,y=2x+6和y=5x哪一个的值先达到20?这说明了什么
结论5: K不同,直线会相交.
y=5x
y=2x+6
y= -x+6
结论6:y=5x先到达20,这说明k值越大,y的变化量越大.
(二)【数形结合 探索发现】
3500
t(分)
S(米)
0
500
起点
1000
1500
2000
3000
60
2500
10
20
40
30
50
70
乌龟
兔子
《新龟兔赛跑》
首尾呼应 问题解决:兔子决定让乌龟先跑2000米 (如图)到底谁会赢?
(三)【师生共析 知识应用】
★1、说出下列函数图象所经过的象限,并说明?随着x值的变化,y的值在怎样变化.
(1)y=2x (2)y= -4x+3
★★★2、看图象,确定一次函数y=kx+b(k≠0) 中k,b的符号。
o
x
y
o
x
y
o
x
y
K>0 b>0
K<0 b>0
K<0 b<0
(四)【分层练习 整合提升】
★1.比一比,看谁画得快
一次函数的图象如图所示,你能画出函数 的图象吗?
1
2
3
4
5
6
-4
-3
-6
x
y
6
2
1
4
3
5
-1
-1
-6
-3
-2
-4
0
-2
-5
-5
y=x
y=x+4
y=x-5
★★2.判断下列各组直线的位置关系:
(A) 与 ;
(B) 与 .
★★3、.若一次函数y=kx+b中,
y随x的增大而减小,则( )
A.k<0,b<0 B.k<0,b>0
C.k<0,b≠0 D.k<0,b为任意数
D
思维拓展
★★★5、直线y=kx+b经过一、二、四象限,那么直线y=bx+k经过哪些象限?
o
y
x
b
K<0
o
y
x
经过一、三、四象限
K<0
经过一、二、四象限
y=bx+k
b>0
b>0
(五)【知识盛宴 星级评价】
一起来整理所学的知识吧……
本节课我一共摘取了 颗“★”,我认为我这一节课的表现(很棒、一般、 没发挥出来 、 还需努力)
我收获了……
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
