北师大版八年级上册数学 5.9二元一次方程组 回顾与思考 课件(共22张PPT)
文档属性
| 名称 | 北师大版八年级上册数学 5.9二元一次方程组 回顾与思考 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-14 18:31:35 | ||
图片预览






文档简介
(共22张PPT)
北师大 八年级《数学(上)》
第五章难点突破训练
典例分析
(1+35%)x
x – y = 8000
设小明家去年草莓的收入为x元,投资为y元.
– (1+10%)y
= 11800
我们家今年草莓收入多少钱呢?
老李 小明 翠花
老李,没关系,你看我们家去年只净赚8000元,今年却净赚11800元,增加投资值得.
翠花,我算了一下,今年我们家草莓的收入比去年增加了35%,不过投资也增加了10%.
解:设小明家去年草莓的收入为x元,投资为y元.
∴(1+35%)×12000=1.35×12000=16200(元).
解题示范
∴小明家今年草莓的收入为16200元.
(今年收入比去年增加了35%)
【技能要求】“做一题,会一类,通一法”
【习惯养成】解题后要及时反思,提炼方法,提高效率.
∴小明家今年草莓的收入为12000元.
收入–投资
去年净赚8000元
今年净赚11800元
等量关系:
解题反思
老李 小明 翠花
老李,没关系,你看我们家去年只净赚8000元,今年却净赚11800元,增加投资值得.
翠花,我算了一下,今年我们家草莓的收入比去年增加了35%,不过投资也增加了10%.
我们家今年草莓收入多少钱呢?
(1+35%)x
x – y = 8000
设小明家去年草莓的收入为x元,投资为y元.
– (1+10%)y
= 11800
去年净赚8000元
今年净赚11800元
“做一题,会一类,通一法”
转化
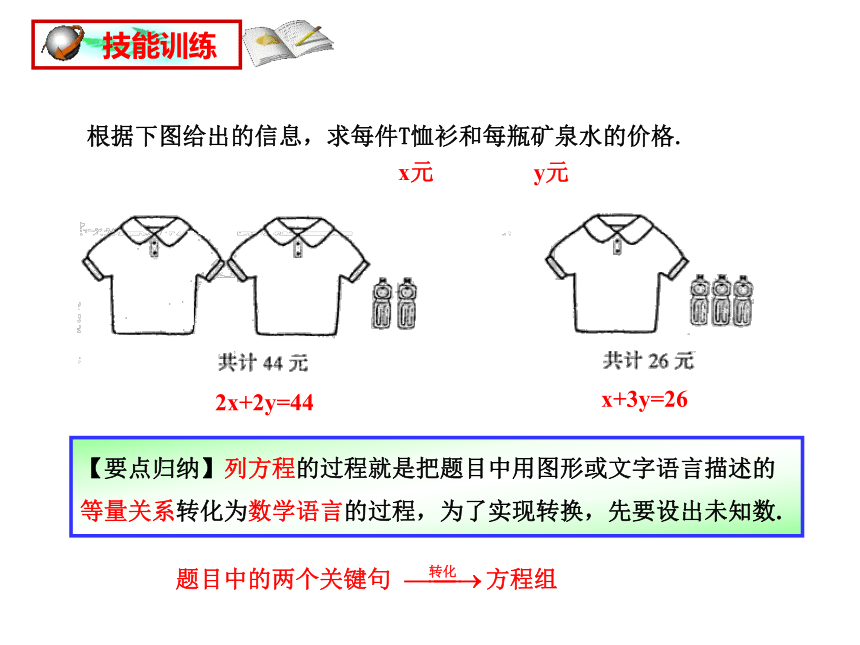
根据下图给出的信息,求每件T恤衫和每瓶矿泉水的价格.
x元
2x+2y=44
x+3y=26
【要点归纳】列方程的过程就是把题目中用图形或文字语言描述的等量关系转化为数学语言的过程,为了实现转换,先要设出未知数.
技能训练
y元
某校七年级⑴⑵两个班共102人去游览该景点,其中⑴班人数较少,不到50人,⑵班人数较多,有50多人.如果两班都以班级为单位分别购票,则一共应付1118元;如果两班联合起来作为一个团体购票,则可以节省不少钱.问两班各有多少名学生?联合起来购票能省多少钱?
(课本P134.18)某景点的门票价格规定如下表:
购票人数 1~50人 51~100人 100人以上
每人门票价 12元 10元 8元
x+ y=102
12x+ 10y=1118
设⑴班x人, ⑵班 y人
回归课本
合作交流
你能利用下面的方程组编几道二元一次方程组的应用题吗?
【方法点拨】注意说清题目中各个数据的实际意义
【创设情境】经济问题、行程问题、分配问题、……
【表达形式】文字、图形、表格
(可以更换数字或运算符号)
阿姨,我买1本笔记本和4支钢笔,共需多少钱?
我买1本笔记本和1支钢笔刚好6元.
刚好18元.
请聪明的你根据图中的对话内容,求出1本笔记本和1支钢笔各需要多少钱?
形式多样
老板
小丽
小亮
售货员
小组合作(定意义,创情境,选形式)
例2、
【2014.茂名.10】如图,设他们中有x个成人,y个儿童.根据图中的对话可得方程组( )
昨天,我们8个人去看电影,买门票花了195元.
每张成人票30元,每张儿童票15元.他们到底去了几个成人、几个儿童?
链接中考
两人搭档(换情境,变数字)
C
【2013.茂名.23⑴】在信宜市某“三华李”种植基地有A、B两个品种的树苗出售,已知A种比B种每株多2元,买1株A种树苗和2株B种树苗共需20元.
问A、B两种树苗每株分别是多少元?
链接中考
x元,y元
x + 2y = 20
x – y = 2
独立完成(换情境,变数字,改符号)
课堂小结
本节课你收获了什么?有什么困惑吗?
【知识提炼】
应用二元一次方程组解决实际问题的基本步骤是:(审)→设→列→解→(验)→答.
【能力提炼】
发现问题→提出问题→分析问题→解决问题→…
【思想提炼】
在水果店里,小李买了苹果5 kg,梨3 kg,老板少要2元,收了50元;老王买了苹果11 kg,梨5 kg,老板按九折收钱,收了90元,该店的苹果和梨的价格各是多少元?
等量关系:⑴5 kg苹果的价钱+3 kg梨的价钱﹣2元=50元;
⑵(11 kg苹果的价钱+5 kg梨的价钱)×0.9=90元.
解:设该店苹果每千克x元,梨每千克y元,
∴该店苹果的单价是每千克5元,梨的单价是每千克9元.
归纳反思
在某个周末,小明和同班同学随他们的父母一同到信宜石根山游玩.
下面是买门票时,小明与他爸爸的对话:
请问:他们一共去了成人和学生各多少人?哪种买票方式更省钱?
设他们共去了x个成人,y个学生,则
35x +35×0.5y = 350
x + y = 12
触类旁通
(图文并茂)
【返回】
开放思维
1、经济问题
⑴第一条方程中的x,y,6表示数量,第二条方程中的系数1,2表示价格,常数10表示费用.
例如,“x+y=6”可以表示为“买笔记本和笔共6份”;
“x+2y=10”可以表示为“买1本笔记本和2支笔共10元”.
例1、某天数学课上有6位同学表现非常积极,吴老师想买一些棒棒糖和钢笔奖励他们,但是口袋里只有10元钱.已知棒棒糖每支1元,钢笔每支2元. 如果每人只奖励一样,钱刚好够用.请问棒棒糖和钢笔各买多少?
⑵x,y表示价格,它们的系数表示数量,常数表示费用.
例如,“x+y=6”可以表示为“买1本笔记本和1支笔共6元”;
“x+2y=10”可以表示为“买1本笔记本和2支笔共10元”.
【编题步骤】创情境,
定意义,
选形式
解题感悟
【编题步骤】创情境,定意义,选形式
买1本笔记本和1支笔共6元,
买1本笔记本和2支笔共10元.
买1本笔记本和1支笔共6元,
买1本笔记本和2支笔共10元.
【解题步骤】找关系,列方程
买1本笔记本和1支笔共6元,
买1本笔记本和2支笔共10元.
í
ì
=
=
.
4
,
2
y
x
【2011.茂名.23⑴】某养鸡场计划购买甲、乙两种小鸡苗共2 000只进行饲养,已知甲种小鸡苗每只2元,乙种小鸡苗每只3元.若购买这批小鸡苗共用了4 500元,求甲、乙两种小鸡苗各购买了多少只?
链接中考4
x只,y只
2x +3y = 4500
x + y = 2000
(课本P134.15)某商场按定价销售某种商品时,每件可获利45元;按定价的八五折销售该商品8件与定价降低35元销售该商品12件所获利润相等.该商品的进价、定价分别是多少?
x元 , y元
y –x=45
8(0.85y–x)
12(y–35–x)
=
回归课本2
(课本P133.8) 某长方形的周长是44cm,若宽的3倍比长多6cm,则长方形的长和宽各是多少?
回归课本3
一个两位数字,个位数字比十位数字大5,如果把这两个数字的位置对换,那么所得的新数与原数的和是143,求这个两位数.
拓展提高1
北师大 八年级《数学(上)》
第五章难点突破训练
典例分析
(1+35%)x
x – y = 8000
设小明家去年草莓的收入为x元,投资为y元.
– (1+10%)y
= 11800
我们家今年草莓收入多少钱呢?
老李 小明 翠花
老李,没关系,你看我们家去年只净赚8000元,今年却净赚11800元,增加投资值得.
翠花,我算了一下,今年我们家草莓的收入比去年增加了35%,不过投资也增加了10%.
解:设小明家去年草莓的收入为x元,投资为y元.
∴(1+35%)×12000=1.35×12000=16200(元).
解题示范
∴小明家今年草莓的收入为16200元.
(今年收入比去年增加了35%)
【技能要求】“做一题,会一类,通一法”
【习惯养成】解题后要及时反思,提炼方法,提高效率.
∴小明家今年草莓的收入为12000元.
收入–投资
去年净赚8000元
今年净赚11800元
等量关系:
解题反思
老李 小明 翠花
老李,没关系,你看我们家去年只净赚8000元,今年却净赚11800元,增加投资值得.
翠花,我算了一下,今年我们家草莓的收入比去年增加了35%,不过投资也增加了10%.
我们家今年草莓收入多少钱呢?
(1+35%)x
x – y = 8000
设小明家去年草莓的收入为x元,投资为y元.
– (1+10%)y
= 11800
去年净赚8000元
今年净赚11800元
“做一题,会一类,通一法”
转化
根据下图给出的信息,求每件T恤衫和每瓶矿泉水的价格.
x元
2x+2y=44
x+3y=26
【要点归纳】列方程的过程就是把题目中用图形或文字语言描述的等量关系转化为数学语言的过程,为了实现转换,先要设出未知数.
技能训练
y元
某校七年级⑴⑵两个班共102人去游览该景点,其中⑴班人数较少,不到50人,⑵班人数较多,有50多人.如果两班都以班级为单位分别购票,则一共应付1118元;如果两班联合起来作为一个团体购票,则可以节省不少钱.问两班各有多少名学生?联合起来购票能省多少钱?
(课本P134.18)某景点的门票价格规定如下表:
购票人数 1~50人 51~100人 100人以上
每人门票价 12元 10元 8元
x+ y=102
12x+ 10y=1118
设⑴班x人, ⑵班 y人
回归课本
合作交流
你能利用下面的方程组编几道二元一次方程组的应用题吗?
【方法点拨】注意说清题目中各个数据的实际意义
【创设情境】经济问题、行程问题、分配问题、……
【表达形式】文字、图形、表格
(可以更换数字或运算符号)
阿姨,我买1本笔记本和4支钢笔,共需多少钱?
我买1本笔记本和1支钢笔刚好6元.
刚好18元.
请聪明的你根据图中的对话内容,求出1本笔记本和1支钢笔各需要多少钱?
形式多样
老板
小丽
小亮
售货员
小组合作(定意义,创情境,选形式)
例2、
【2014.茂名.10】如图,设他们中有x个成人,y个儿童.根据图中的对话可得方程组( )
昨天,我们8个人去看电影,买门票花了195元.
每张成人票30元,每张儿童票15元.他们到底去了几个成人、几个儿童?
链接中考
两人搭档(换情境,变数字)
C
【2013.茂名.23⑴】在信宜市某“三华李”种植基地有A、B两个品种的树苗出售,已知A种比B种每株多2元,买1株A种树苗和2株B种树苗共需20元.
问A、B两种树苗每株分别是多少元?
链接中考
x元,y元
x + 2y = 20
x – y = 2
独立完成(换情境,变数字,改符号)
课堂小结
本节课你收获了什么?有什么困惑吗?
【知识提炼】
应用二元一次方程组解决实际问题的基本步骤是:(审)→设→列→解→(验)→答.
【能力提炼】
发现问题→提出问题→分析问题→解决问题→…
【思想提炼】
在水果店里,小李买了苹果5 kg,梨3 kg,老板少要2元,收了50元;老王买了苹果11 kg,梨5 kg,老板按九折收钱,收了90元,该店的苹果和梨的价格各是多少元?
等量关系:⑴5 kg苹果的价钱+3 kg梨的价钱﹣2元=50元;
⑵(11 kg苹果的价钱+5 kg梨的价钱)×0.9=90元.
解:设该店苹果每千克x元,梨每千克y元,
∴该店苹果的单价是每千克5元,梨的单价是每千克9元.
归纳反思
在某个周末,小明和同班同学随他们的父母一同到信宜石根山游玩.
下面是买门票时,小明与他爸爸的对话:
请问:他们一共去了成人和学生各多少人?哪种买票方式更省钱?
设他们共去了x个成人,y个学生,则
35x +35×0.5y = 350
x + y = 12
触类旁通
(图文并茂)
【返回】
开放思维
1、经济问题
⑴第一条方程中的x,y,6表示数量,第二条方程中的系数1,2表示价格,常数10表示费用.
例如,“x+y=6”可以表示为“买笔记本和笔共6份”;
“x+2y=10”可以表示为“买1本笔记本和2支笔共10元”.
例1、某天数学课上有6位同学表现非常积极,吴老师想买一些棒棒糖和钢笔奖励他们,但是口袋里只有10元钱.已知棒棒糖每支1元,钢笔每支2元. 如果每人只奖励一样,钱刚好够用.请问棒棒糖和钢笔各买多少?
⑵x,y表示价格,它们的系数表示数量,常数表示费用.
例如,“x+y=6”可以表示为“买1本笔记本和1支笔共6元”;
“x+2y=10”可以表示为“买1本笔记本和2支笔共10元”.
【编题步骤】创情境,
定意义,
选形式
解题感悟
【编题步骤】创情境,定意义,选形式
买1本笔记本和1支笔共6元,
买1本笔记本和2支笔共10元.
买1本笔记本和1支笔共6元,
买1本笔记本和2支笔共10元.
【解题步骤】找关系,列方程
买1本笔记本和1支笔共6元,
买1本笔记本和2支笔共10元.
í
ì
=
=
.
4
,
2
y
x
【2011.茂名.23⑴】某养鸡场计划购买甲、乙两种小鸡苗共2 000只进行饲养,已知甲种小鸡苗每只2元,乙种小鸡苗每只3元.若购买这批小鸡苗共用了4 500元,求甲、乙两种小鸡苗各购买了多少只?
链接中考4
x只,y只
2x +3y = 4500
x + y = 2000
(课本P134.15)某商场按定价销售某种商品时,每件可获利45元;按定价的八五折销售该商品8件与定价降低35元销售该商品12件所获利润相等.该商品的进价、定价分别是多少?
x元 , y元
y –x=45
8(0.85y–x)
12(y–35–x)
=
回归课本2
(课本P133.8) 某长方形的周长是44cm,若宽的3倍比长多6cm,则长方形的长和宽各是多少?
回归课本3
一个两位数字,个位数字比十位数字大5,如果把这两个数字的位置对换,那么所得的新数与原数的和是143,求这个两位数.
拓展提高1
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
