4.3.2 角的比较与运算 课件(共39张PPT)
文档属性
| 名称 | 4.3.2 角的比较与运算 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 21:08:18 | ||
图片预览






文档简介
(共39张PPT)
第四章 图形初步认识
4.3.2 角的比较与运算
4.3 角
学习目标
学习目标
1.掌握角的大小的比较方法.
2.理解角平分线和角的和、差、倍、分的意义及数量关系,能够用几何语言进行相关表述,并能解答相关问题.
3.会进行涉及度、分、秒的角度的计算.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
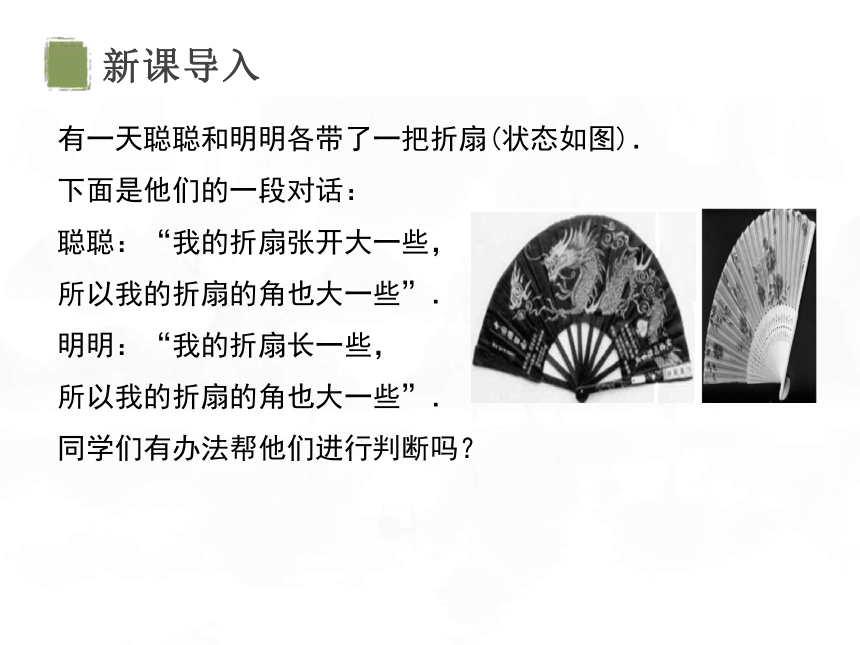
有一天聪聪和明明各带了一把折扇(状态如图).
下面是他们的一段对话:
聪聪:“我的折扇张开大一些,
所以我的折扇的角也大一些”.
明明:“我的折扇长一些,
所以我的折扇的角也大一些”.
同学们有办法帮他们进行判断吗?
讲授新知
贰
讲授新知
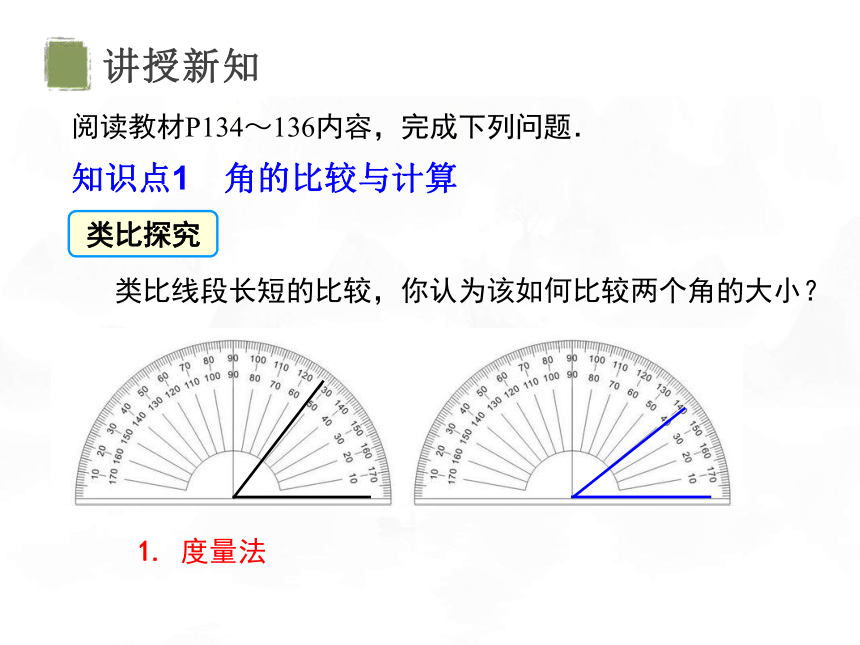
阅读教材P134~136内容,完成下列问题.
知识点1 角的比较与计算
类比线段长短的比较,你认为该如何比较两个角的大小?
1. 度量法
类比探究
讲授新知
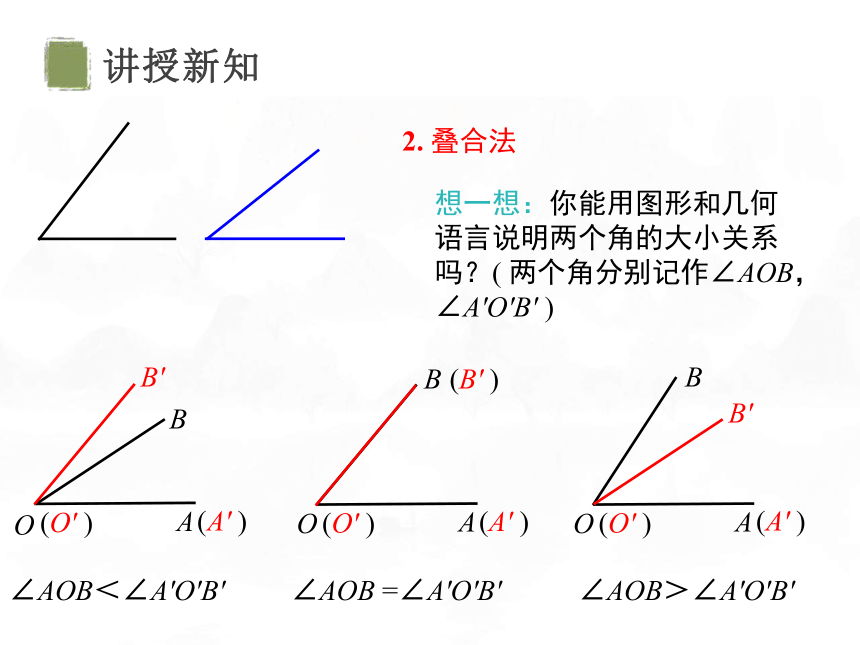
2. 叠合法
A
B
O
(O' )
B'
(A' )
A
B
O
A
B
O
想一想:你能用图形和几何语言说明两个角的大小关系吗?( 两个角分别记作∠AOB,∠A'O'B' )
(O' )
B'
(A' )
∠AOB<∠A'O'B'
∠AOB =∠A'O'B'
∠AOB>∠A'O'B'
(O' )
(B' )
(A' )
讲授新知
图中有几个角?它们之间有什么关系?
图中有3个角:∠AOC,∠AOB,∠BOC.
∠AOC 是∠AOB 与∠BOC的和,记作∠AOC = ∠AOB +∠BOC;
它们的关系:
∠AOB 是∠AOC与∠BOC的差,
记作∠AOB = ∠AOC-∠BOC;
类似地,∠AOC-∠AOB= .
观察与思考
∠BOC
A
B
O
C
讲授新知
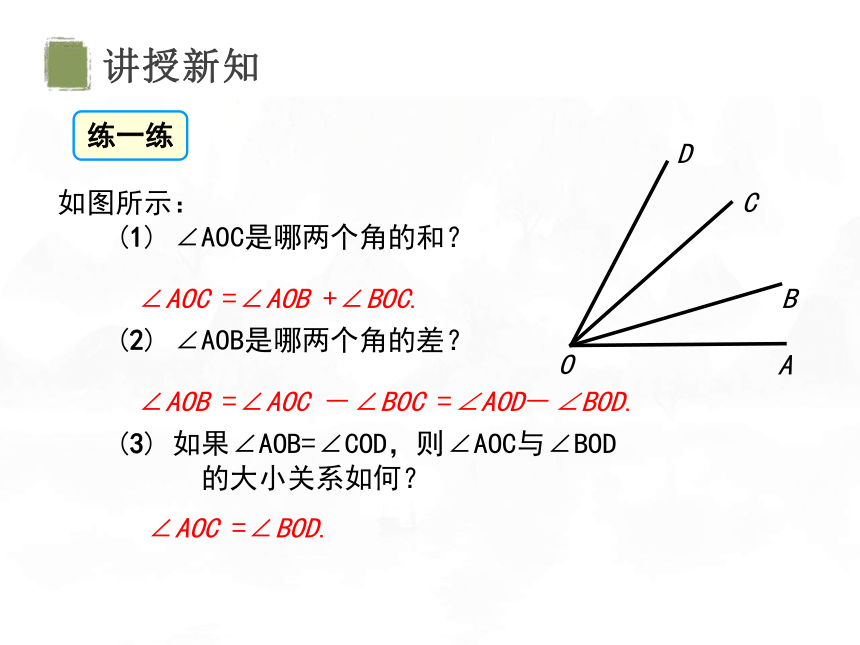
练一练
如图所示:
(1) ∠AOC是哪两个角的和?
(2) ∠AOB是哪两个角的差?
(3) 如果∠AOB=∠COD,则∠AOC与∠BOD
的大小关系如何?
B
A
O
C
D
∠AOC =∠AOB +∠BOC.
∠AOB =∠AOC -∠BOC =∠AOD-∠BOD.
∠AOC =∠BOD.
范例应用
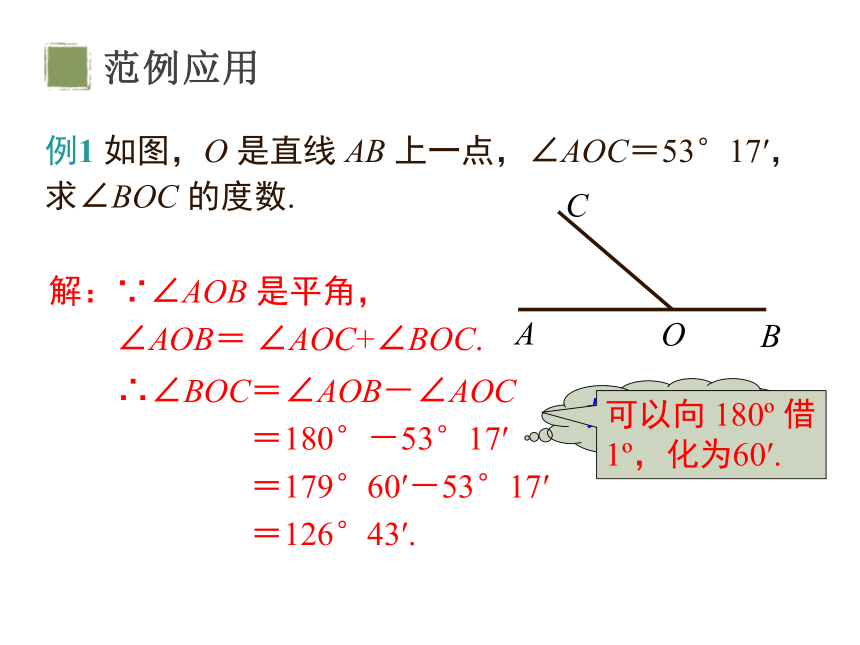
例1 如图,O 是直线 AB 上一点,∠AOC=53°17′,
求∠BOC 的度数.
解:∵∠AOB 是平角,
∠AOB= ∠AOC+∠BOC.
∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=179°60′-53°17′
=126°43′.
O
C
B
A
如何计算?
可以向 180 借
1 ,化为60′.
范例应用
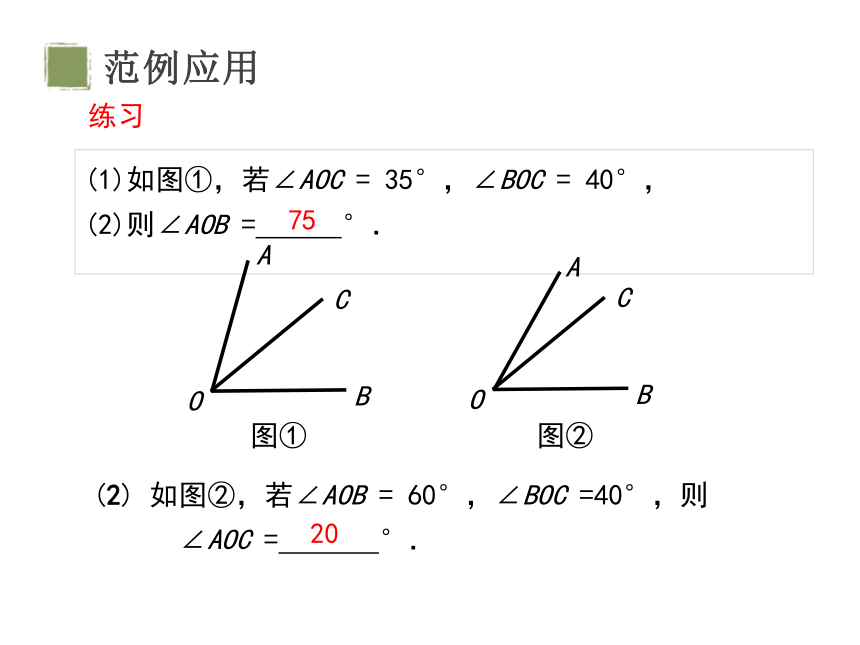
(2) 如图②,若∠AOB = 60°,∠BOC =40°,则
∠AOC = °.
如图①,若∠AOC = 35°,∠BOC = 40°,
则∠AOB = °.
75
20
A
B
O
C
A
B
O
C
图① 图②
练习
范例应用
(3) 若∠AOB =60°,∠AOC =30°,则∠BOC
= °.
90或30
O
B
A
C
C
提示:无图条件下要分情况讨论.
范例应用
如图,借助一副三角尺可以画出15°和75°的角,你还能画出哪些度数的角?
试一试:
75°
15°
范例应用
例2 把一个周角 7 等分,每一份是多少度的角 (精确到分)?
解:360°÷7 = 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.
有余数,可以把度的余数化成分后再除
范例应用
例3 计算:
(1)153°29′42″+26°40′32″;
(2)110°36′-90°37′28″;
(3)62°24′17″×4;
(4)102°43′21″÷3.
解:(1)原式=179°69′74″=180°10′14″;
(2)原式=109°95′60″-90°37′28″=19°58′32″;
范例应用
(3)原式=248°96′68″=249°37′8″;
(4)原式=102°42′81″÷3=34°14′27″.
方法总结:角度的运算规律为:(1)加减法时将同一单位进行加减,加法够60进1,减法不够减要借1当60;(2)乘法时将数与度、分、秒分别相乘,然后从小到大逢60进1;(3)除法时用度先除,把余数化为分,再加上原来的分,用这个数除以除数,把余数化成秒,再加上原来的秒,再用这个数除以除数,如果除不尽,就按题意要求,进行四舍五入.
讲授新课
知识点2 角的平分线
互动探究
B
A
O
C
动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
讲授新课
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
O
B
A
C
∵ OC是∠AOB 的角平分线,
∴ ∠AOC =∠BOC = ∠AOB,∠AOB =2∠BOC =2∠AOC.
范例应用
例4 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?
解:因为 OB 平分∠AOC,
∠AOC=80°,
O
A
B
C
D
E
所以
∠BOC= ∠AOC
= ×80°=40°.
范例应用
(2) 如果∠AOB=40°,∠DOE=30°,那么∠BOD
是多少度?
解:因为 OB 平分∠AOC,
所以 ∠BOC=∠AOB = 40°.
因为 OD 平分∠COE,
所以∠COD=∠DOE = 30°,
所以
∠BOD =∠BOC+∠COD = 40°+30°= 70°.
O
A
B
C
D
E
范例应用
(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB
是多少度?
解:因为 ∠COD=30°,
OD 平分∠COE,
所以 ∠COE=2∠COD=60°,
所以 ∠AOC=∠AOE-∠COE
=140°-60°= 80°.
又因为 OB 平分∠AOC,
O
A
B
C
D
E
所以
∠AOB= ∠AOC= ×80°= 40°.
范例应用
例5 如图,已知∠AOB=40°,自O点引射线OC,若∠AOC:∠COB=2:3.求OC与∠AOB的平分线所成的角的度数.
O
A
B
解:分以下两种情况:
设∠AOC=2x,∠COB=3x,
∵∠AOB=40°,∴2x+3x=40°,得x=8°,
∴∠AOC=2x=2×8°=16°.
∵OD平分∠AOB,∴∠AOD=20°,
∴∠COD=∠AOD-∠AOC=20°-16°=4°.
C
D
如图,OC在∠AOB内部,OD平分∠AOB,
范例应用
∴设∠AOC=2x,∠COB=3x,
∵∠AOB=40°,
∴3x-2x=40°,得x=40°,
∴∠AOC=2x=2×40°=80°,
∵OD平分∠AOB,∴∠AOD=20°,
∴∠COD=∠AOC+∠AOD=80°+20°=100°.
O
A
B
C
D
如图,OC在∠AOB外部,OD平分∠AOB,
∴OC与∠AOB的平分线所成的角的度数为4°或100°.
范例应用
方法总结:涉及到角度的计算时,除常规的和差倍分计算外,通常还需运用方程思想和分类讨论思想解决问题.
范例应用
1. 如图:OC是∠AOB的平分线,OD是∠BOC的平
分线,那么下列各式中正确的是 ( )
A
做一做
O
A
B
C
D
范例应用
2. 如图,OC是平角∠AOB的角平分线,∠COD=32°,
求∠AOD的度数.
答案:∠AOD=122°.
O
A
B
C
D
当堂训练
叁
当堂训练
1.如右图,已知∠AOB=∠COD,则( )
A.∠1>∠2 B.∠1=∠2
C.∠1<∠2 D.∠1与∠2的大小无法比较
B
2.如右图,OC是∠AOB的平分线,OD是∠BOC的平分线.若∠AOB=120°,则∠AOD的度数为( )
A.30° B.50° C.60° D.90°
D
当堂训练
3. 如图,OC为∠AOB内部的一条射线.若∠AOB=100°,∠1=25°,则∠2的度数为 .
75°
4. 如图,∠AOB=90°,OD、OE分别是∠BOC和∠AOC的平分线.若∠BOE=30°,则∠DOE的度数为 °.
45°
当堂训练
5.计算下列各题:
(1)98°45′36″+71°22′34″;
(2)52°37′-31°45′12″;
(3)13°24′15″×5;
(4)58°34′16″÷4.
解:(1)原式=170°8′10″.
(2)原式=20°51′48″.
(3)原式=67°1′15″.
(4)原式=14°38′34″.
当堂训练
6.如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1)求∠EOD的度数;
(2)若∠BOC=90°,求∠AOE的度数.
解:(1)∵∠AOB=120°,OD平分∠BOC,OE平分∠AOC,
∴∠EOD=∠DOC+∠EOC= (∠BOC+∠AOC )= ∠AOB= ×120°=60°.
当堂训练
(2)∵∠AOB=120°,∠BOC=90°,
∴∠AOC=120°-90°=30°.
∵OE平分∠AOC,
∴∠AOE= ∠AOC= ×30°=15°.
课堂小结
肆
课堂小结
壹
角的比较
度量法
叠合法
角的运算
加与减
乘与除
角的和差倍分关系
角的计算
课后作业
基础题:1.课后习题 第 4,5,6题。
提高题:2.课后习题 第 14,15题。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第四章 图形初步认识
4.3.2 角的比较与运算
4.3 角
学习目标
学习目标
1.掌握角的大小的比较方法.
2.理解角平分线和角的和、差、倍、分的意义及数量关系,能够用几何语言进行相关表述,并能解答相关问题.
3.会进行涉及度、分、秒的角度的计算.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
有一天聪聪和明明各带了一把折扇(状态如图).
下面是他们的一段对话:
聪聪:“我的折扇张开大一些,
所以我的折扇的角也大一些”.
明明:“我的折扇长一些,
所以我的折扇的角也大一些”.
同学们有办法帮他们进行判断吗?
讲授新知
贰
讲授新知
阅读教材P134~136内容,完成下列问题.
知识点1 角的比较与计算
类比线段长短的比较,你认为该如何比较两个角的大小?
1. 度量法
类比探究
讲授新知
2. 叠合法
A
B
O
(O' )
B'
(A' )
A
B
O
A
B
O
想一想:你能用图形和几何语言说明两个角的大小关系吗?( 两个角分别记作∠AOB,∠A'O'B' )
(O' )
B'
(A' )
∠AOB<∠A'O'B'
∠AOB =∠A'O'B'
∠AOB>∠A'O'B'
(O' )
(B' )
(A' )
讲授新知
图中有几个角?它们之间有什么关系?
图中有3个角:∠AOC,∠AOB,∠BOC.
∠AOC 是∠AOB 与∠BOC的和,记作∠AOC = ∠AOB +∠BOC;
它们的关系:
∠AOB 是∠AOC与∠BOC的差,
记作∠AOB = ∠AOC-∠BOC;
类似地,∠AOC-∠AOB= .
观察与思考
∠BOC
A
B
O
C
讲授新知
练一练
如图所示:
(1) ∠AOC是哪两个角的和?
(2) ∠AOB是哪两个角的差?
(3) 如果∠AOB=∠COD,则∠AOC与∠BOD
的大小关系如何?
B
A
O
C
D
∠AOC =∠AOB +∠BOC.
∠AOB =∠AOC -∠BOC =∠AOD-∠BOD.
∠AOC =∠BOD.
范例应用
例1 如图,O 是直线 AB 上一点,∠AOC=53°17′,
求∠BOC 的度数.
解:∵∠AOB 是平角,
∠AOB= ∠AOC+∠BOC.
∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=179°60′-53°17′
=126°43′.
O
C
B
A
如何计算?
可以向 180 借
1 ,化为60′.
范例应用
(2) 如图②,若∠AOB = 60°,∠BOC =40°,则
∠AOC = °.
如图①,若∠AOC = 35°,∠BOC = 40°,
则∠AOB = °.
75
20
A
B
O
C
A
B
O
C
图① 图②
练习
范例应用
(3) 若∠AOB =60°,∠AOC =30°,则∠BOC
= °.
90或30
O
B
A
C
C
提示:无图条件下要分情况讨论.
范例应用
如图,借助一副三角尺可以画出15°和75°的角,你还能画出哪些度数的角?
试一试:
75°
15°
范例应用
例2 把一个周角 7 等分,每一份是多少度的角 (精确到分)?
解:360°÷7 = 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.
有余数,可以把度的余数化成分后再除
范例应用
例3 计算:
(1)153°29′42″+26°40′32″;
(2)110°36′-90°37′28″;
(3)62°24′17″×4;
(4)102°43′21″÷3.
解:(1)原式=179°69′74″=180°10′14″;
(2)原式=109°95′60″-90°37′28″=19°58′32″;
范例应用
(3)原式=248°96′68″=249°37′8″;
(4)原式=102°42′81″÷3=34°14′27″.
方法总结:角度的运算规律为:(1)加减法时将同一单位进行加减,加法够60进1,减法不够减要借1当60;(2)乘法时将数与度、分、秒分别相乘,然后从小到大逢60进1;(3)除法时用度先除,把余数化为分,再加上原来的分,用这个数除以除数,把余数化成秒,再加上原来的秒,再用这个数除以除数,如果除不尽,就按题意要求,进行四舍五入.
讲授新课
知识点2 角的平分线
互动探究
B
A
O
C
动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
讲授新课
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
O
B
A
C
∵ OC是∠AOB 的角平分线,
∴ ∠AOC =∠BOC = ∠AOB,∠AOB =2∠BOC =2∠AOC.
范例应用
例4 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?
解:因为 OB 平分∠AOC,
∠AOC=80°,
O
A
B
C
D
E
所以
∠BOC= ∠AOC
= ×80°=40°.
范例应用
(2) 如果∠AOB=40°,∠DOE=30°,那么∠BOD
是多少度?
解:因为 OB 平分∠AOC,
所以 ∠BOC=∠AOB = 40°.
因为 OD 平分∠COE,
所以∠COD=∠DOE = 30°,
所以
∠BOD =∠BOC+∠COD = 40°+30°= 70°.
O
A
B
C
D
E
范例应用
(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB
是多少度?
解:因为 ∠COD=30°,
OD 平分∠COE,
所以 ∠COE=2∠COD=60°,
所以 ∠AOC=∠AOE-∠COE
=140°-60°= 80°.
又因为 OB 平分∠AOC,
O
A
B
C
D
E
所以
∠AOB= ∠AOC= ×80°= 40°.
范例应用
例5 如图,已知∠AOB=40°,自O点引射线OC,若∠AOC:∠COB=2:3.求OC与∠AOB的平分线所成的角的度数.
O
A
B
解:分以下两种情况:
设∠AOC=2x,∠COB=3x,
∵∠AOB=40°,∴2x+3x=40°,得x=8°,
∴∠AOC=2x=2×8°=16°.
∵OD平分∠AOB,∴∠AOD=20°,
∴∠COD=∠AOD-∠AOC=20°-16°=4°.
C
D
如图,OC在∠AOB内部,OD平分∠AOB,
范例应用
∴设∠AOC=2x,∠COB=3x,
∵∠AOB=40°,
∴3x-2x=40°,得x=40°,
∴∠AOC=2x=2×40°=80°,
∵OD平分∠AOB,∴∠AOD=20°,
∴∠COD=∠AOC+∠AOD=80°+20°=100°.
O
A
B
C
D
如图,OC在∠AOB外部,OD平分∠AOB,
∴OC与∠AOB的平分线所成的角的度数为4°或100°.
范例应用
方法总结:涉及到角度的计算时,除常规的和差倍分计算外,通常还需运用方程思想和分类讨论思想解决问题.
范例应用
1. 如图:OC是∠AOB的平分线,OD是∠BOC的平
分线,那么下列各式中正确的是 ( )
A
做一做
O
A
B
C
D
范例应用
2. 如图,OC是平角∠AOB的角平分线,∠COD=32°,
求∠AOD的度数.
答案:∠AOD=122°.
O
A
B
C
D
当堂训练
叁
当堂训练
1.如右图,已知∠AOB=∠COD,则( )
A.∠1>∠2 B.∠1=∠2
C.∠1<∠2 D.∠1与∠2的大小无法比较
B
2.如右图,OC是∠AOB的平分线,OD是∠BOC的平分线.若∠AOB=120°,则∠AOD的度数为( )
A.30° B.50° C.60° D.90°
D
当堂训练
3. 如图,OC为∠AOB内部的一条射线.若∠AOB=100°,∠1=25°,则∠2的度数为 .
75°
4. 如图,∠AOB=90°,OD、OE分别是∠BOC和∠AOC的平分线.若∠BOE=30°,则∠DOE的度数为 °.
45°
当堂训练
5.计算下列各题:
(1)98°45′36″+71°22′34″;
(2)52°37′-31°45′12″;
(3)13°24′15″×5;
(4)58°34′16″÷4.
解:(1)原式=170°8′10″.
(2)原式=20°51′48″.
(3)原式=67°1′15″.
(4)原式=14°38′34″.
当堂训练
6.如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1)求∠EOD的度数;
(2)若∠BOC=90°,求∠AOE的度数.
解:(1)∵∠AOB=120°,OD平分∠BOC,OE平分∠AOC,
∴∠EOD=∠DOC+∠EOC= (∠BOC+∠AOC )= ∠AOB= ×120°=60°.
当堂训练
(2)∵∠AOB=120°,∠BOC=90°,
∴∠AOC=120°-90°=30°.
∵OE平分∠AOC,
∴∠AOE= ∠AOC= ×30°=15°.
课堂小结
肆
课堂小结
壹
角的比较
度量法
叠合法
角的运算
加与减
乘与除
角的和差倍分关系
角的计算
课后作业
基础题:1.课后习题 第 4,5,6题。
提高题:2.课后习题 第 14,15题。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
