3.1.1 一元一次方程 课件(37张PPT)
文档属性
| 名称 | 3.1.1 一元一次方程 课件(37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 00:00:00 | ||
图片预览








文档简介
(共37张PPT)
第三章 一元一次方程
3.1.1 一元一次方程
3.1 从算式到方程
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
鸡兔同笼问题:
今有雉兔同笼,上有三十五头,下有九十四足,
问雉兔各几何?
你有哪些方法解决这道经典有趣的数学题?
新课导入
温故知新
小学我们已经学过简易方程,你能判断出下列各式哪些是方程吗?
(1)5x+3y-6x=37( ) (2)4x-7( )
(3)5x≥3( ) (4)6x +x-2=0( )
(5)1+2=3( ) (6) -m=11( )
含有未知数的等式叫做方程.
√
√
√
×
×
×
讲授新知
贰
讲授新知
阅读教材P78~80内容,完成下列问题.
知识点1 方程及一元一次方程的概念
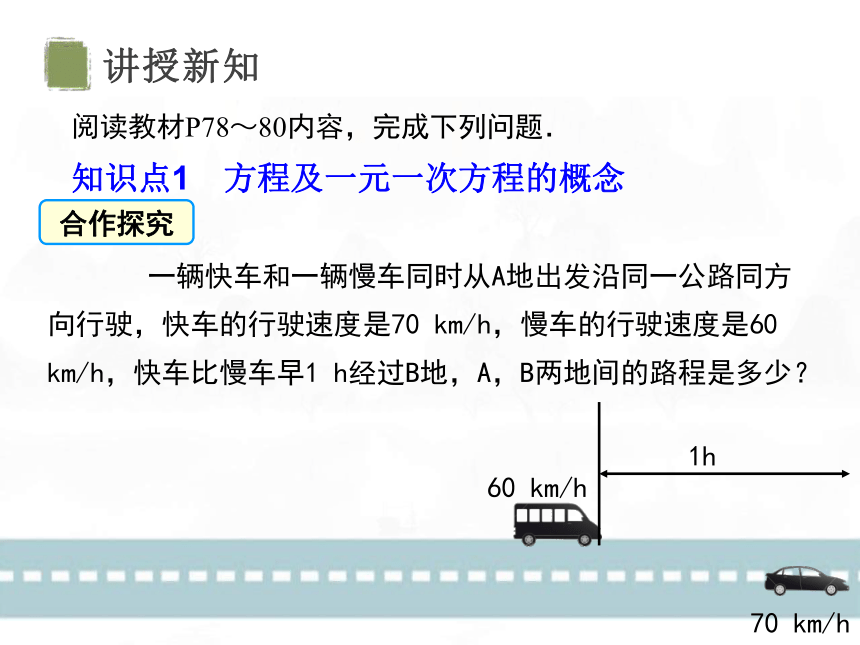
一辆快车和一辆慢车同时从A地出发沿同一公路同方向行驶,快车的行驶速度是70 km/h,慢车的行驶速度是60 km/h,快车比慢车早1 h经过B地,A,B两地间的路程是多少?
合作探究
1h
60 km/h
70 km/h
讲授新知
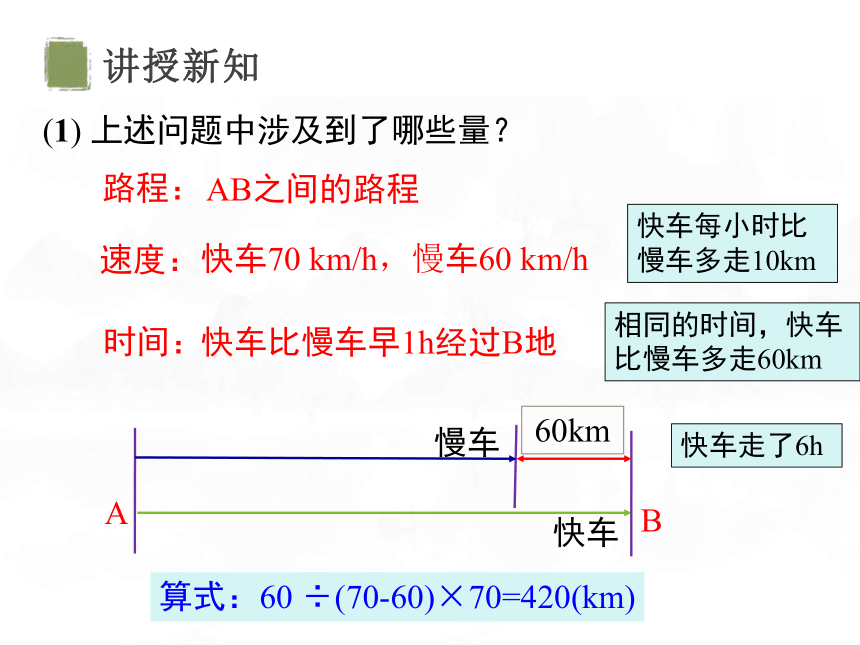
(1) 上述问题中涉及到了哪些量?
快车70 km/h,慢车60 km/h
快车比慢车早1h经过B地
AB之间的路程
速度:
时间:
路程:
A
B
快车
慢车
1h
快车每小时比慢车多走10km
60km
相同的时间,快车比慢车多走60km
快车走了6h
算式:60 ÷(70-60)×70=420(km)
讲授新知
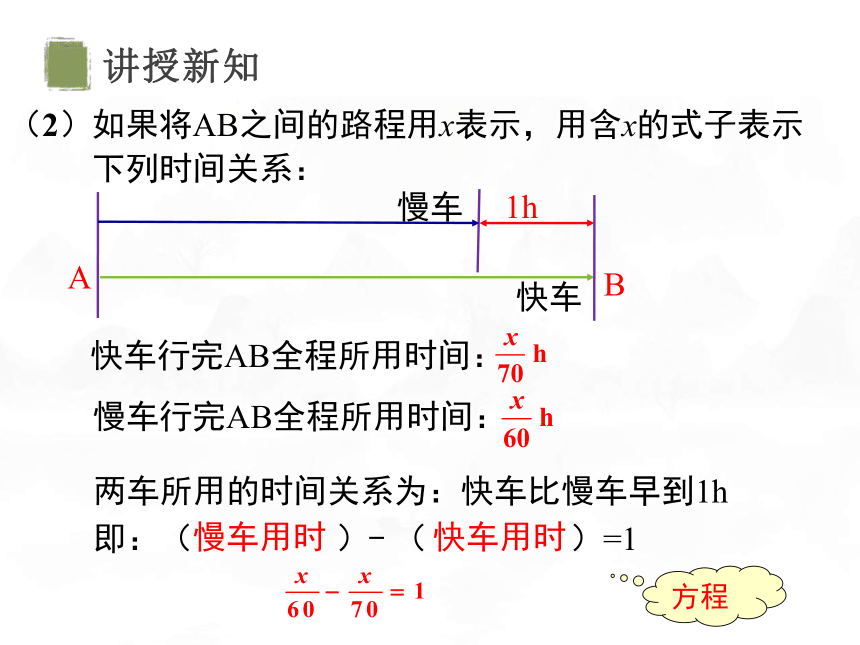
(2)如果将AB之间的路程用x表示,用含x的式子表示
下列时间关系:
快车行完AB全程所用时间:
慢车行完AB全程所用时间:
两车所用的时间关系为:快车比慢车早到1h
即:( )- ( )=1
慢车用时
快车用时
方程
A
B
快车
慢车
1h
讲授新知
(3)如果用y表示快车行完AB的总时间,你能从
快车与慢车的路程关系中找到等量关系,从
而列出方程吗?
方 程: 70 y =60(y+1)
等量关系:快车y小时路程=慢车(y+1)小时路程
A
B
快车
慢车
1h
讲授新知
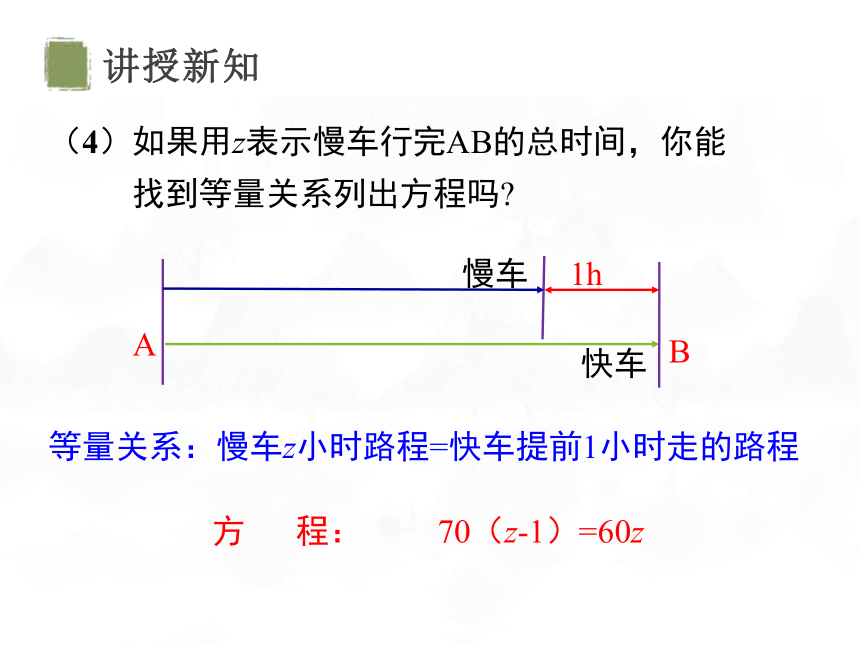
(4)如果用z表示慢车行完AB的总时间,你能
找到等量关系列出方程吗
方 程: 70(z-1)=60z
等量关系:慢车z小时路程=快车提前1小时走的路程
A
B
快车
慢车
1h
讲授新知
比较:列算式和列方程
从算式到方程是数学的进步!
列算式:列出的算式表示解题的计算过程, 只能用已知数.对于较复杂的问题,列算式比较困难.
列方程:方程是根据题中的等量关系列出的等式. 既可用已知数,又可用未知数,解决问题比较方便.
讲授新知
观察下列方程,它们有什么共同点?
70 y=60(y+1)
70(z-1)=60z
问题1 每个方程中,各含有几个未知数?
问题2 说一说每个方程中未知数的次数.
问题3 等号两边的式子有什么共同点?
1个
1次
都是整式
讲授新知
知识要点
这样的方程叫做一元一次方程.
等号两边都是整式,
(一次)
只含有一个未知数,
(一元)
未知数的次数都是1,
一元一次方程
范例应用
例1 下列方程中是一元一次方程的有( )
A.x+3=y+2 B.1-3(1-2x)=-2(5-3x)
C.x-1= D. -2=2y-7
【方法归纳】判断一元一次方程需满足三个条件:(1)只含有一个未知数;(2)未知数的次数是1;(3)是整式方程.
D
范例应用
下列哪些是一元一次方程?
(1) ; (2) ;
(3) ;(4) ;
(5) ; (6) ;
(7) .
√
√
练一练
范例应用
例2 方程(m+1)x|m|+1=0是关于x的一元一次方程,则( )
A.m=±1 B.m=1
C.m=-1 D.m≠-1
B
【方法归纳】一元一次方程中求字母的值,需谨记两个条件:①未知数的次数为1;②未知数的系数不为0.
解析:由一元一次方程的概念,一元一次方程必须满足未知数的次数为1且系数不等于0,所以 ,解得m=1.故选B.
范例应用
【练习】
若关于x的方程 是一元一次方程,
则n的值为 .
2或-2
讲授新课
知识点2 根据实际问题列方程
例3 根据下列问题,设未知数并列出方程:
(1)用一根长24 cm的铁丝围成一个正方形,正方形的边长是多少?
解:设正方形的边长为x cm.
等量关系:正方形边长×4=周长,
列方程:4x=24.
讲授新课
(2)一台计算机已使用1700 h,预计每月再使用150h,经过多少月这台计算机的使用时间达到规定的检修时间2450h?
解:设x月后这台计算机的使用时间达到2450 h.
等量关系:已用时间+再用时间=检修时间,
列方程:1700+150x=2450.
讲授新课
(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?
解:设这个学校的学生人数为x,那么女生人数为0.52x,男生人数为(1-0.52)x.等量关系:女生人数-男生人数=80,
列方程:0.52x-(1-052)x=80.
【方法归纳】解题的关键是正确理解题意,设出未知数,找到题目当中的等量关系,列方程.
讲授新课
【练习】
某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“6·1”儿童节举行文具优惠售卖活动,铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.求卖出铅笔的支数.
解:设卖出铅笔x支,则卖出圆珠笔(60-x)支.
等量关系:x支铅笔的售价1.2×0.8x,(60-x)支圆珠笔的售价=2×0.9(60-x),
列方程:
讲授新课
知识点3 方程的解
对于方程4x=24,容易知道 x=6可以使等式成立, 对于方程 170+15x=245,你知道x等于什么时,等式成立吗?我们来试一试.
x 1 2 3 4 5 6 …
…
我们知道当x=5时,170+15x的值是245,所以方程 170+15x = 245中的未知数的值应是5.
185
200
215
230
245
260
170+15x
讲授新课
使方程左右两边相等的未知数的值叫方程的解.求方程解的过程叫做解方程.
x=420是 方程的解吗
知识要点
方程的解
范例应用
例4 x=1000和x=2000中哪一个是方程 0.52x-(1-0.52)x
=80的解?
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,
右边=80,左边≠右边,所以x=1000不是此方程的解.
当x=2000时,
方程左边= 0.52×2000-(1-0.52)×2000=1040-960=80,
右边=80,左边=右边,所以x=2000是此方程的解.
范例应用
1. 将数值代入方程左边进行计算,
2. 将数值代入方程右边进行计算,
判断一个数值是不是方程的解的步骤:
方法归纳
范例应用
练一练
检验 x = 3是不是方程 2x-3 = 5x-15的解.
解:把 x =3分别代入方程的左边和右边,得
当x = 4,5,6时呢
左边=2×3-3=3,
右边=5×3-15=0.
∵左边≠右边,
∴ x =3不是方程的解.
当堂训练
叁
当堂训练
1.下列方程中,解是x=-5的是( )
A.x-2=7 B.2x-6=-4
C.2+3x=-13 D.x-1=16
2.若x=1是方程ax+3x=2的解,则a的值是( )
A.-1 B.5 C.1 D.-5
3.某校学生种植一批树苗,若每人种10棵,则剩下6棵树苗未种;若每人种12棵,则缺6棵树苗.若设参与种树的有x人,则可列方程为( )
A.10x-6=12x+6 B.10x+6=12x-6
C.10x+6=12x+6 D.10x-6=12x-6
B
A
C
当堂训练
4.下列方程: ; ; ; ;
.其中是方程的是 ,是一元一次方程的是 .(填序号)
①②③④⑤
②③
5.若方程(|m|-2)x2-(m+2)x-6=0是关于x的一元一次方程.
(1)求m的值;
(2)判断x=3,x=- ,x= 是不是方程的解.
当堂训练
解:(1)因为方程(|m|-2)x2-(m+2)x-6=0是关于x的一元一次方程,
所以|m|-2=0,则m=±2.又因为m+2≠0,即m≠-2,所以m=2.
(2)由(1)知原方程为-4x-6=0.当x=- 时,-4x-6=0;
当x=3或x= 时,-4x-6≠0,故x=- 是方程的解,x=3,x= 不是方程的解.
课堂小结
肆
课堂小结
壹
一元一次方程
定义
只含有一个未知数,未知数的次数是1,等号两边都是整式
方程的解
解方程就是求出使方程中等号两边相等的未知数的值
课后作业
基础题:1.课后习题 第 1,2,3题。
提高题:2.课后习题 第 6,9,10题。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第三章 一元一次方程
3.1.1 一元一次方程
3.1 从算式到方程
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
鸡兔同笼问题:
今有雉兔同笼,上有三十五头,下有九十四足,
问雉兔各几何?
你有哪些方法解决这道经典有趣的数学题?
新课导入
温故知新
小学我们已经学过简易方程,你能判断出下列各式哪些是方程吗?
(1)5x+3y-6x=37( ) (2)4x-7( )
(3)5x≥3( ) (4)6x +x-2=0( )
(5)1+2=3( ) (6) -m=11( )
含有未知数的等式叫做方程.
√
√
√
×
×
×
讲授新知
贰
讲授新知
阅读教材P78~80内容,完成下列问题.
知识点1 方程及一元一次方程的概念
一辆快车和一辆慢车同时从A地出发沿同一公路同方向行驶,快车的行驶速度是70 km/h,慢车的行驶速度是60 km/h,快车比慢车早1 h经过B地,A,B两地间的路程是多少?
合作探究
1h
60 km/h
70 km/h
讲授新知
(1) 上述问题中涉及到了哪些量?
快车70 km/h,慢车60 km/h
快车比慢车早1h经过B地
AB之间的路程
速度:
时间:
路程:
A
B
快车
慢车
1h
快车每小时比慢车多走10km
60km
相同的时间,快车比慢车多走60km
快车走了6h
算式:60 ÷(70-60)×70=420(km)
讲授新知
(2)如果将AB之间的路程用x表示,用含x的式子表示
下列时间关系:
快车行完AB全程所用时间:
慢车行完AB全程所用时间:
两车所用的时间关系为:快车比慢车早到1h
即:( )- ( )=1
慢车用时
快车用时
方程
A
B
快车
慢车
1h
讲授新知
(3)如果用y表示快车行完AB的总时间,你能从
快车与慢车的路程关系中找到等量关系,从
而列出方程吗?
方 程: 70 y =60(y+1)
等量关系:快车y小时路程=慢车(y+1)小时路程
A
B
快车
慢车
1h
讲授新知
(4)如果用z表示慢车行完AB的总时间,你能
找到等量关系列出方程吗
方 程: 70(z-1)=60z
等量关系:慢车z小时路程=快车提前1小时走的路程
A
B
快车
慢车
1h
讲授新知
比较:列算式和列方程
从算式到方程是数学的进步!
列算式:列出的算式表示解题的计算过程, 只能用已知数.对于较复杂的问题,列算式比较困难.
列方程:方程是根据题中的等量关系列出的等式. 既可用已知数,又可用未知数,解决问题比较方便.
讲授新知
观察下列方程,它们有什么共同点?
70 y=60(y+1)
70(z-1)=60z
问题1 每个方程中,各含有几个未知数?
问题2 说一说每个方程中未知数的次数.
问题3 等号两边的式子有什么共同点?
1个
1次
都是整式
讲授新知
知识要点
这样的方程叫做一元一次方程.
等号两边都是整式,
(一次)
只含有一个未知数,
(一元)
未知数的次数都是1,
一元一次方程
范例应用
例1 下列方程中是一元一次方程的有( )
A.x+3=y+2 B.1-3(1-2x)=-2(5-3x)
C.x-1= D. -2=2y-7
【方法归纳】判断一元一次方程需满足三个条件:(1)只含有一个未知数;(2)未知数的次数是1;(3)是整式方程.
D
范例应用
下列哪些是一元一次方程?
(1) ; (2) ;
(3) ;(4) ;
(5) ; (6) ;
(7) .
√
√
练一练
范例应用
例2 方程(m+1)x|m|+1=0是关于x的一元一次方程,则( )
A.m=±1 B.m=1
C.m=-1 D.m≠-1
B
【方法归纳】一元一次方程中求字母的值,需谨记两个条件:①未知数的次数为1;②未知数的系数不为0.
解析:由一元一次方程的概念,一元一次方程必须满足未知数的次数为1且系数不等于0,所以 ,解得m=1.故选B.
范例应用
【练习】
若关于x的方程 是一元一次方程,
则n的值为 .
2或-2
讲授新课
知识点2 根据实际问题列方程
例3 根据下列问题,设未知数并列出方程:
(1)用一根长24 cm的铁丝围成一个正方形,正方形的边长是多少?
解:设正方形的边长为x cm.
等量关系:正方形边长×4=周长,
列方程:4x=24.
讲授新课
(2)一台计算机已使用1700 h,预计每月再使用150h,经过多少月这台计算机的使用时间达到规定的检修时间2450h?
解:设x月后这台计算机的使用时间达到2450 h.
等量关系:已用时间+再用时间=检修时间,
列方程:1700+150x=2450.
讲授新课
(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?
解:设这个学校的学生人数为x,那么女生人数为0.52x,男生人数为(1-0.52)x.等量关系:女生人数-男生人数=80,
列方程:0.52x-(1-052)x=80.
【方法归纳】解题的关键是正确理解题意,设出未知数,找到题目当中的等量关系,列方程.
讲授新课
【练习】
某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“6·1”儿童节举行文具优惠售卖活动,铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.求卖出铅笔的支数.
解:设卖出铅笔x支,则卖出圆珠笔(60-x)支.
等量关系:x支铅笔的售价1.2×0.8x,(60-x)支圆珠笔的售价=2×0.9(60-x),
列方程:
讲授新课
知识点3 方程的解
对于方程4x=24,容易知道 x=6可以使等式成立, 对于方程 170+15x=245,你知道x等于什么时,等式成立吗?我们来试一试.
x 1 2 3 4 5 6 …
…
我们知道当x=5时,170+15x的值是245,所以方程 170+15x = 245中的未知数的值应是5.
185
200
215
230
245
260
170+15x
讲授新课
使方程左右两边相等的未知数的值叫方程的解.求方程解的过程叫做解方程.
x=420是 方程的解吗
知识要点
方程的解
范例应用
例4 x=1000和x=2000中哪一个是方程 0.52x-(1-0.52)x
=80的解?
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,
右边=80,左边≠右边,所以x=1000不是此方程的解.
当x=2000时,
方程左边= 0.52×2000-(1-0.52)×2000=1040-960=80,
右边=80,左边=右边,所以x=2000是此方程的解.
范例应用
1. 将数值代入方程左边进行计算,
2. 将数值代入方程右边进行计算,
判断一个数值是不是方程的解的步骤:
方法归纳
范例应用
练一练
检验 x = 3是不是方程 2x-3 = 5x-15的解.
解:把 x =3分别代入方程的左边和右边,得
当x = 4,5,6时呢
左边=2×3-3=3,
右边=5×3-15=0.
∵左边≠右边,
∴ x =3不是方程的解.
当堂训练
叁
当堂训练
1.下列方程中,解是x=-5的是( )
A.x-2=7 B.2x-6=-4
C.2+3x=-13 D.x-1=16
2.若x=1是方程ax+3x=2的解,则a的值是( )
A.-1 B.5 C.1 D.-5
3.某校学生种植一批树苗,若每人种10棵,则剩下6棵树苗未种;若每人种12棵,则缺6棵树苗.若设参与种树的有x人,则可列方程为( )
A.10x-6=12x+6 B.10x+6=12x-6
C.10x+6=12x+6 D.10x-6=12x-6
B
A
C
当堂训练
4.下列方程: ; ; ; ;
.其中是方程的是 ,是一元一次方程的是 .(填序号)
①②③④⑤
②③
5.若方程(|m|-2)x2-(m+2)x-6=0是关于x的一元一次方程.
(1)求m的值;
(2)判断x=3,x=- ,x= 是不是方程的解.
当堂训练
解:(1)因为方程(|m|-2)x2-(m+2)x-6=0是关于x的一元一次方程,
所以|m|-2=0,则m=±2.又因为m+2≠0,即m≠-2,所以m=2.
(2)由(1)知原方程为-4x-6=0.当x=- 时,-4x-6=0;
当x=3或x= 时,-4x-6≠0,故x=- 是方程的解,x=3,x= 不是方程的解.
课堂小结
肆
课堂小结
壹
一元一次方程
定义
只含有一个未知数,未知数的次数是1,等号两边都是整式
方程的解
解方程就是求出使方程中等号两边相等的未知数的值
课后作业
基础题:1.课后习题 第 1,2,3题。
提高题:2.课后习题 第 6,9,10题。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
