3.1.2 从算式到方程 第2课时 等式的性质 课件(共37张PPT)
文档属性
| 名称 | 3.1.2 从算式到方程 第2课时 等式的性质 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 21:06:47 | ||
图片预览











文档简介
(共37张PPT)
3.1.2 等式的性质
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
对比天平与等式,你有什么发现?
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡.
等号
等式的左边
等式的右边
情境引入
讲授新知
贰
讲授新知
阅读教材P81~82内容,完成下列问题.
知识点1 等式的性质
观察天平有什么特性?
天平两边同时加入相同质量的砝码
天平仍然平衡
天平两边同时拿去相同质量的砝码
天平仍然平衡
讲授新知
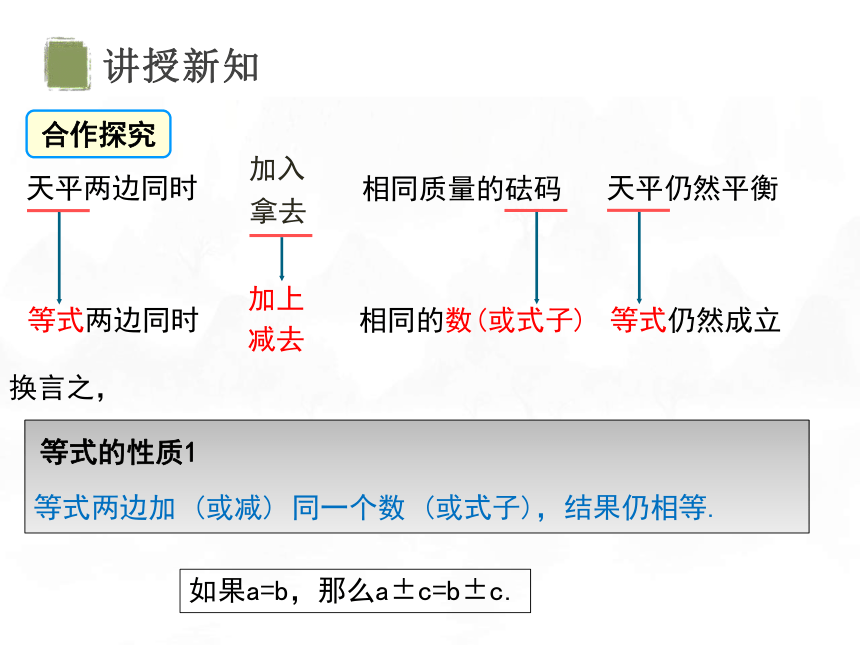
天平两边同时
天平仍然平衡
加入
拿去
相同质量的砝码
相同的数(或式子)
等式两边同时
加上
减去
等式仍然成立
换言之,
等式两边加 (或减) 同一个数 (或式子),结果仍相等.
如果a=b,那么a±c=b±c.
合作探究
等式的性质1
讲授新知
由天平看等式的性质2
讲授新知
讲授新知
讲授新知
讲授新知
讲授新知
讲授新知
讲授新知
讲授新知
讲授新知
讲授新知
讲授新知
你能发现什么规律?
讲授新知
等式两边乘同一个数,或除以同一个不为0的数,结
果仍相等.
等式的性质2
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
范例应用
(2) 怎样从等式 3+x=1 得到等式 x =-2
(3) 怎样从等式 4x=12 得到等式 x =3
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘 .
依据等式的性质2两边同时除以 或同乘100.
例1 (1) 怎样从等式 x-5= y-5 得到等式 x = y
依据等式的性质1两边同时加5.
(4) 怎样从等式 得到等式 a = b
范例应用
例2 已知mx=my,下列结论错误的是 ( )
A. x=y B. a+mx=a+my
C. mx-y=my-y D. amx=amy
分析:A、等式的两边都除以m,根据等式性质2,m≠0,而A选项没有说明,故A错误;B、符合等式的性质1,正确.C、符合等式的性质1,正确.D、符合等式的性质1,正确.故选A.
A
【方法归纳】本题主要考查等式的基本性质.在等式的两边同时加上或减去同一个数或字母,等式仍成立,这里的数或字母没有条件限制,但是在等式的两边同时乘以或除以同一个数或字母时,这里的数或字母必须不为0.
范例应用
(2) 从 a+2=b+2 能不能得到 a=b,为什么
(3) 从-3a=-3b 能不能得到 a=b,为什么
(4) 从 3ac=4a 能不能得到 3c=4,为什么
(1) 从 x = y 能不能得到 ,为什么
能,根据等式的性质2,两边同时除以9
能,根据等式的性质1,两边同时加上2
能,根据等式的性质2,两边同时除以-3
不能,a可能为0
练习
讲授新课
知识点2 利用等式的性质解方程
例3 利用等式的性质解下列方程:
(1)x+6=17;
解:方程两边同时减6,
得 x=9.
(2)-3x=15;
解:方程两边同时除以-3,
得x=-5.
讲授新课
(3)2x-1=-3;
解:方程两边同时加1,
得2x=-2,
方程两边同时除以2,
得x=-1.
解:方程两边同时减1,得
x=-3,
方程两边同时乘-3,
得x=9.
讲授新课
练习
(1) x+6 = 17 ;
(2) -3x = 15 ;
(4)
(3) 2x-1 = -3 ;
解:(1)两边同时减去6,得x=11.
(2)两边同时除以-3,得x=-5.
(3)两边同时加上1,得2x=-2.
两边同时除以2,得x=-1.
(4)两边同时加上-1,得
两边同时乘以-3,得x=9.
当堂训练
叁
当堂训练
1.若a=b,m是任意有理数,则下列等式不一定成立的是( )
A.a+m=b+m B.a-m=b-m
C.am=bm D.
2.将3x-7=2x变形正确的是( )
A.3x+2x=7 B.3x-2x=-7
C.3x+2x=-7 D.3x-2x=7
D
D
当堂训练
3.下列方程的变形,符合等式性质的是( )
A.由2x-3=7得2x=7-3
B.由2x-3=x-1得2x-x=-1-3
C.由-3x=5得x=5+3
D.由-x=1得x=-4
D
当堂训练
4.用适当的数或整式填空,使所得的式子仍是等式,并注明根据.
(1)如果x+2=3,那么x=3+ ,根据是 ;
(2)如果4x=3x-7,那么4x- =-7,根据是 ;
(3)如果-2x=6,那么x= ,根据是 .
(-2)
等式的性质1
等式的性质1
3x
-3
等式的性质2
当堂训练
5. 应用等式的性质解下列方程并检验:
(1) x+3= 6; (2) 0.2x =4;
(3) -2x+4=0; (4)
解: (1) x =3; (2) x =20;
(4)x =-4.
课堂小结
肆
课堂小结
等式的
基本性质
基本性质1
基本性质2
应用
如果a=b,那么a±c=b±c.
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
运用等式的性质把方程“化归”为最简的形式 x = a
课后作业
基础题:1.课后习题 第 4题。
提高题:2.课后习题 第 11题。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.1.2 等式的性质
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
对比天平与等式,你有什么发现?
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡.
等号
等式的左边
等式的右边
情境引入
讲授新知
贰
讲授新知
阅读教材P81~82内容,完成下列问题.
知识点1 等式的性质
观察天平有什么特性?
天平两边同时加入相同质量的砝码
天平仍然平衡
天平两边同时拿去相同质量的砝码
天平仍然平衡
讲授新知
天平两边同时
天平仍然平衡
加入
拿去
相同质量的砝码
相同的数(或式子)
等式两边同时
加上
减去
等式仍然成立
换言之,
等式两边加 (或减) 同一个数 (或式子),结果仍相等.
如果a=b,那么a±c=b±c.
合作探究
等式的性质1
讲授新知
由天平看等式的性质2
讲授新知
讲授新知
讲授新知
讲授新知
讲授新知
讲授新知
讲授新知
讲授新知
讲授新知
讲授新知
讲授新知
你能发现什么规律?
讲授新知
等式两边乘同一个数,或除以同一个不为0的数,结
果仍相等.
等式的性质2
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
范例应用
(2) 怎样从等式 3+x=1 得到等式 x =-2
(3) 怎样从等式 4x=12 得到等式 x =3
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘 .
依据等式的性质2两边同时除以 或同乘100.
例1 (1) 怎样从等式 x-5= y-5 得到等式 x = y
依据等式的性质1两边同时加5.
(4) 怎样从等式 得到等式 a = b
范例应用
例2 已知mx=my,下列结论错误的是 ( )
A. x=y B. a+mx=a+my
C. mx-y=my-y D. amx=amy
分析:A、等式的两边都除以m,根据等式性质2,m≠0,而A选项没有说明,故A错误;B、符合等式的性质1,正确.C、符合等式的性质1,正确.D、符合等式的性质1,正确.故选A.
A
【方法归纳】本题主要考查等式的基本性质.在等式的两边同时加上或减去同一个数或字母,等式仍成立,这里的数或字母没有条件限制,但是在等式的两边同时乘以或除以同一个数或字母时,这里的数或字母必须不为0.
范例应用
(2) 从 a+2=b+2 能不能得到 a=b,为什么
(3) 从-3a=-3b 能不能得到 a=b,为什么
(4) 从 3ac=4a 能不能得到 3c=4,为什么
(1) 从 x = y 能不能得到 ,为什么
能,根据等式的性质2,两边同时除以9
能,根据等式的性质1,两边同时加上2
能,根据等式的性质2,两边同时除以-3
不能,a可能为0
练习
讲授新课
知识点2 利用等式的性质解方程
例3 利用等式的性质解下列方程:
(1)x+6=17;
解:方程两边同时减6,
得 x=9.
(2)-3x=15;
解:方程两边同时除以-3,
得x=-5.
讲授新课
(3)2x-1=-3;
解:方程两边同时加1,
得2x=-2,
方程两边同时除以2,
得x=-1.
解:方程两边同时减1,得
x=-3,
方程两边同时乘-3,
得x=9.
讲授新课
练习
(1) x+6 = 17 ;
(2) -3x = 15 ;
(4)
(3) 2x-1 = -3 ;
解:(1)两边同时减去6,得x=11.
(2)两边同时除以-3,得x=-5.
(3)两边同时加上1,得2x=-2.
两边同时除以2,得x=-1.
(4)两边同时加上-1,得
两边同时乘以-3,得x=9.
当堂训练
叁
当堂训练
1.若a=b,m是任意有理数,则下列等式不一定成立的是( )
A.a+m=b+m B.a-m=b-m
C.am=bm D.
2.将3x-7=2x变形正确的是( )
A.3x+2x=7 B.3x-2x=-7
C.3x+2x=-7 D.3x-2x=7
D
D
当堂训练
3.下列方程的变形,符合等式性质的是( )
A.由2x-3=7得2x=7-3
B.由2x-3=x-1得2x-x=-1-3
C.由-3x=5得x=5+3
D.由-x=1得x=-4
D
当堂训练
4.用适当的数或整式填空,使所得的式子仍是等式,并注明根据.
(1)如果x+2=3,那么x=3+ ,根据是 ;
(2)如果4x=3x-7,那么4x- =-7,根据是 ;
(3)如果-2x=6,那么x= ,根据是 .
(-2)
等式的性质1
等式的性质1
3x
-3
等式的性质2
当堂训练
5. 应用等式的性质解下列方程并检验:
(1) x+3= 6; (2) 0.2x =4;
(3) -2x+4=0; (4)
解: (1) x =3; (2) x =20;
(4)x =-4.
课堂小结
肆
课堂小结
等式的
基本性质
基本性质1
基本性质2
应用
如果a=b,那么a±c=b±c.
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
运用等式的性质把方程“化归”为最简的形式 x = a
课后作业
基础题:1.课后习题 第 4题。
提高题:2.课后习题 第 11题。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
