3.4 第1课时 配套、工程问题 课件(共34张PPT)
文档属性
| 名称 | 3.4 第1课时 配套、工程问题 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 21:40:09 | ||
图片预览










文档简介
(共34张PPT)
第三章 一元一次方程
第1课时 配套、工程问题
3.4 实际问题与一元一次方程
学习目标
学习目标
1.以“探究”的形式讨论如何用一元一次方程解决实际问题;
2.体会一元一次方程与实际生活的密切联系,加强数学建模思想的应用意识;
3.培养运用一元一次方程分析和解决实际问题的能力.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
前面我们学习了一元一次方程的解法,本节课,我们将讨论一元一次方程的应用. 生活中,有很多需要进行配套的问题,如课桌和凳子、螺钉和螺母、电扇叶片和电机等,大家能举出生活中配套问题的例子吗?
讲授新知
贰
讲授新知
阅读教材P100~101内容,完成下列问题.
知识点1 产品配套问题
填一填:
某厂欲制作一些方桌和椅子,1张方桌与4把椅子刚好配成一套,为了使桌椅刚好配套,商家应制作椅子的数量是桌子数量的 倍. 方桌与椅子的数量之比是 .
4
1:4
范例应用
例1 某车间有22名工人,每人每天可以生产1 200个螺钉或2000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
想一想:本题需要我们解决的问题是什么?
题目中哪些信息能解决人员安排的问题?
螺母和螺钉的数量关系如何?
如果设x名工人生产螺母,怎样列方程?
范例应用
列表分析:
产品类型 生产人数 单人产量 总产量
螺钉 x 1200
螺母 2000
×
=
1200 x
人数和为22人
22-x
螺母总产量是螺钉的2倍
×
=
2000(22-x)
等量关系:螺母总量=螺钉总量×2
范例应用
解:设应安排 x 名工人生产螺钉,(22-x)名工人生
产螺母.
依题意,得
2000(22-x)=2×1200x .
解方程,得 x=10.
所以 22-x=12.
答:应安排10名工人生产螺钉,12名工人生产
螺母.
还有别的方法吗?
范例应用
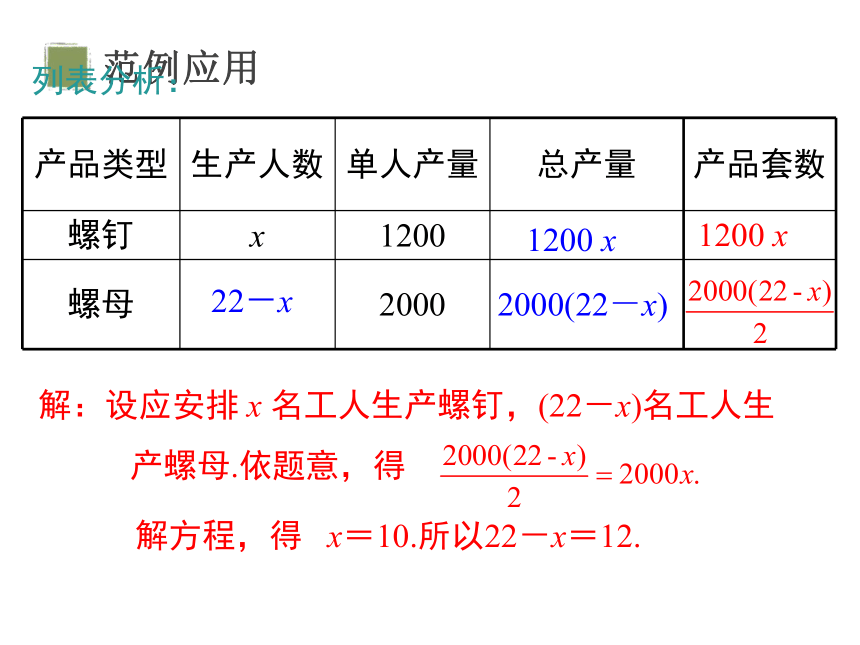
列表分析:
产品类型 生产人数 单人产量 总产量 产品套数
螺钉 x 1200
螺母 2000
1200 x
22-x
2000(22-x)
1200 x
解:设应安排 x 名工人生产螺钉,(22-x)名工人生
产螺母.依题意,得
解方程,得 x=10.所以22-x=12.
范例应用
【方法归纳】
生产调配问题通常从调配后各量之间的倍、分关系寻找相等关系,建立方程.解决配套问题的思路:
1.利用配套问题中物品之间具有的数量关系作为列方程的依据;
2.利用配套问题中的套数不变作为列方程的依据.
范例应用
【练习】
某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼.制作1块大月饼要用0.05 kg面粉,1块小月饼要用0.02 kg面粉.现共有面粉4500 kg,问制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
解:设用x kg面粉制作大月饼,则用(4500-x) kg面粉制作小月饼.
根据题意得 ,
解得x=2500,则4500-2500=2000(kg).
答:用2500 kg面粉制作大月饼,2000 kg面粉制作小月饼,才能生产最多的盒装月饼.
讲授新课
知识点2 工程问题
填一填
1.一件工作,甲独做需要6天完成,乙独做需要5天完成.
(1)若把工作总量设为1,则甲的工作效率(甲一天完成的工作量)是 ,乙的工作效率是 .
(2)甲做x天完成的工作量是 ,乙做x天完成的工作量是 ,甲乙合做x天完成的工作量是 .
讲授新课
议一议
工程问题中,涉及哪些量?它们之间有什么数量关系?
(1)工程问题中,涉及的量有工作量、 ;
(2)请写出这些量之间存在的数量关系:
.
工作效率、工作时间
工作量=工作效率×工作时间
范例应用
如果把总工作量设为1,则人均效率 (一个人 1 h 完
成的工作量) 为 ,
x人先做 4h 完成的工作量为 ,
增加 2 人后再做 8h 完成的工作量为 ,
这两
个工作量之和等于 .
例2 整理一批图书,由一个人做要 40 h 完成. 现计划由一部分人先做 4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应先安排多少人工作?
分析:在工程问题中:工作量=人均效率×人数×时
间;工作总量=各部分工作量之和.
总工作量
如果设先安排 x人做4 h,你能列出方程吗?
范例应用
人均效率 人数 时间 工作量
前一部分工作 x 4
后一部分工作 x+2 8
×
×
=
工作量之和等于总工作量1
×
=
×
范例应用
解:设先安排 x 人做4 h,根据题意得等量关系:
可列方程
解方程,得
4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 小时.
前部分工作总量+后部分工作总量=总工作量1
范例应用
例4 加工某种工件,甲单独作要20天完成,乙只要10天就能完成任务,现在要求二人在12天内完成任务.问乙需工作几天后甲再继续加工才可正好按期完成任务?
效率 时间 工作量
甲
乙
x
12-x
范例应用
解:设乙需工作x天后甲再继续加工才可正好按期完成任务,则甲做了(12-x)天.
依题意,得
解得 x=8.
答:乙需工作8天后甲再继续加工才可正好按期完成任务.
范例应用
想一想:若要求二人在8天内完成任务,乙先加工几天后,甲加入合作加工,恰好能如期完成任务?
效率 时间 工作量
甲
乙
8
x
范例应用
解:设甲加工x天,两人如期完成任务,则在甲加入之前,乙先工作了(8-x)天.
依题意,得
解得x=4,则8-x=4.
答:乙需加工4天后,甲加入合作加工才可正好按期完成任务.
范例应用
【方法归纳】
解决工程问题的基本思路:
1. 三个基本量:工作量、工作效率、工作时间.它们之间的关系是:工作量=工作效率×工作时间.
2.相等关系:工作总量=各部分工作量之和.(1) 按工作时间,工作总量=各时间段的工作量之和;(2) 按工作者,工作总量=各工作者的工作量之和.
3.通常在没有具体数值的情况下,把工作总量看作1.
当堂训练
叁
当堂训练
1.41人参加运土劳动,有30根扁担,安排多少人抬,多少人挑,可使扁担和人数相配不多不少?若设有x人挑土,则可列方程是( )
A.2-(30-)=41 B.+(41-)=30
C.+ =30 D.30-=41-
2.一项工程甲独做20天可以完成,乙独做30天可以完成.现在两个人合做,但是乙中途因事离开几天,从开工后14天把这项工作做完,则乙中途离开了( )
A.10天 B.9天 C.7天 D.5天
C
D
当堂训练
3.在某大型活动中,志愿者们手上、脖子上的丝巾非常美丽.车间70名工人承接了制作丝巾的任务,已知每人每天平均生产手上的丝巾1800条或者脖子上的丝巾1200条,一条脖子上的丝巾要配两条手上的丝巾.为了使每天生产的丝巾刚好配套,应分配多少名工人生产脖子上的丝巾,多少名工人生产手上的丝巾?
解:设应分配x名工人生产脖子上的丝巾,
分配(70-x)名工人生产手上的丝巾.
由题意得1800(70-x)=2×1200x,
解得x=30,则70-x=70-30=40.
答:应分配30名工人生产脖子上的丝巾,40名工人生产手上的丝巾.
当堂训练
4. 一件工作,甲单独做20小时完成,乙单独做12小时
完成,现在先由甲单独做4小时,剩下的部分由甲、
乙合做. 剩下的部分需要几小时完成?
解:设剩下的部分需要x小时完成,根据题意得:
解得x = 6.
答:剩下的部分需要6小时完成.
当堂训练
5. 一个道路工程,甲队单独施工9天完成,乙队单独
做24天完成.现在甲乙两队共同施工3天,因甲另
有任务,剩下的工程由乙队完成,问乙队还需几
天才能完成?
解:设乙队还需x天才能完成,由题意得:
解得 x = 13.
答:乙队还需13天才能完成.
课堂小结
肆
课堂小结
用一元一次方程解决实际问题的基本过程如下:
实际问题
设未知数,列方程
一元一次方程
实际问题的答案
解方程
一元一次方程的解
(x=a)
检验
课后作业
基础题:1.课后习题 第 2,5题。
提高题:2.课后习题 第 9,12题。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第三章 一元一次方程
第1课时 配套、工程问题
3.4 实际问题与一元一次方程
学习目标
学习目标
1.以“探究”的形式讨论如何用一元一次方程解决实际问题;
2.体会一元一次方程与实际生活的密切联系,加强数学建模思想的应用意识;
3.培养运用一元一次方程分析和解决实际问题的能力.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
前面我们学习了一元一次方程的解法,本节课,我们将讨论一元一次方程的应用. 生活中,有很多需要进行配套的问题,如课桌和凳子、螺钉和螺母、电扇叶片和电机等,大家能举出生活中配套问题的例子吗?
讲授新知
贰
讲授新知
阅读教材P100~101内容,完成下列问题.
知识点1 产品配套问题
填一填:
某厂欲制作一些方桌和椅子,1张方桌与4把椅子刚好配成一套,为了使桌椅刚好配套,商家应制作椅子的数量是桌子数量的 倍. 方桌与椅子的数量之比是 .
4
1:4
范例应用
例1 某车间有22名工人,每人每天可以生产1 200个螺钉或2000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
想一想:本题需要我们解决的问题是什么?
题目中哪些信息能解决人员安排的问题?
螺母和螺钉的数量关系如何?
如果设x名工人生产螺母,怎样列方程?
范例应用
列表分析:
产品类型 生产人数 单人产量 总产量
螺钉 x 1200
螺母 2000
×
=
1200 x
人数和为22人
22-x
螺母总产量是螺钉的2倍
×
=
2000(22-x)
等量关系:螺母总量=螺钉总量×2
范例应用
解:设应安排 x 名工人生产螺钉,(22-x)名工人生
产螺母.
依题意,得
2000(22-x)=2×1200x .
解方程,得 x=10.
所以 22-x=12.
答:应安排10名工人生产螺钉,12名工人生产
螺母.
还有别的方法吗?
范例应用
列表分析:
产品类型 生产人数 单人产量 总产量 产品套数
螺钉 x 1200
螺母 2000
1200 x
22-x
2000(22-x)
1200 x
解:设应安排 x 名工人生产螺钉,(22-x)名工人生
产螺母.依题意,得
解方程,得 x=10.所以22-x=12.
范例应用
【方法归纳】
生产调配问题通常从调配后各量之间的倍、分关系寻找相等关系,建立方程.解决配套问题的思路:
1.利用配套问题中物品之间具有的数量关系作为列方程的依据;
2.利用配套问题中的套数不变作为列方程的依据.
范例应用
【练习】
某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼.制作1块大月饼要用0.05 kg面粉,1块小月饼要用0.02 kg面粉.现共有面粉4500 kg,问制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
解:设用x kg面粉制作大月饼,则用(4500-x) kg面粉制作小月饼.
根据题意得 ,
解得x=2500,则4500-2500=2000(kg).
答:用2500 kg面粉制作大月饼,2000 kg面粉制作小月饼,才能生产最多的盒装月饼.
讲授新课
知识点2 工程问题
填一填
1.一件工作,甲独做需要6天完成,乙独做需要5天完成.
(1)若把工作总量设为1,则甲的工作效率(甲一天完成的工作量)是 ,乙的工作效率是 .
(2)甲做x天完成的工作量是 ,乙做x天完成的工作量是 ,甲乙合做x天完成的工作量是 .
讲授新课
议一议
工程问题中,涉及哪些量?它们之间有什么数量关系?
(1)工程问题中,涉及的量有工作量、 ;
(2)请写出这些量之间存在的数量关系:
.
工作效率、工作时间
工作量=工作效率×工作时间
范例应用
如果把总工作量设为1,则人均效率 (一个人 1 h 完
成的工作量) 为 ,
x人先做 4h 完成的工作量为 ,
增加 2 人后再做 8h 完成的工作量为 ,
这两
个工作量之和等于 .
例2 整理一批图书,由一个人做要 40 h 完成. 现计划由一部分人先做 4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应先安排多少人工作?
分析:在工程问题中:工作量=人均效率×人数×时
间;工作总量=各部分工作量之和.
总工作量
如果设先安排 x人做4 h,你能列出方程吗?
范例应用
人均效率 人数 时间 工作量
前一部分工作 x 4
后一部分工作 x+2 8
×
×
=
工作量之和等于总工作量1
×
=
×
范例应用
解:设先安排 x 人做4 h,根据题意得等量关系:
可列方程
解方程,得
4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 小时.
前部分工作总量+后部分工作总量=总工作量1
范例应用
例4 加工某种工件,甲单独作要20天完成,乙只要10天就能完成任务,现在要求二人在12天内完成任务.问乙需工作几天后甲再继续加工才可正好按期完成任务?
效率 时间 工作量
甲
乙
x
12-x
范例应用
解:设乙需工作x天后甲再继续加工才可正好按期完成任务,则甲做了(12-x)天.
依题意,得
解得 x=8.
答:乙需工作8天后甲再继续加工才可正好按期完成任务.
范例应用
想一想:若要求二人在8天内完成任务,乙先加工几天后,甲加入合作加工,恰好能如期完成任务?
效率 时间 工作量
甲
乙
8
x
范例应用
解:设甲加工x天,两人如期完成任务,则在甲加入之前,乙先工作了(8-x)天.
依题意,得
解得x=4,则8-x=4.
答:乙需加工4天后,甲加入合作加工才可正好按期完成任务.
范例应用
【方法归纳】
解决工程问题的基本思路:
1. 三个基本量:工作量、工作效率、工作时间.它们之间的关系是:工作量=工作效率×工作时间.
2.相等关系:工作总量=各部分工作量之和.(1) 按工作时间,工作总量=各时间段的工作量之和;(2) 按工作者,工作总量=各工作者的工作量之和.
3.通常在没有具体数值的情况下,把工作总量看作1.
当堂训练
叁
当堂训练
1.41人参加运土劳动,有30根扁担,安排多少人抬,多少人挑,可使扁担和人数相配不多不少?若设有x人挑土,则可列方程是( )
A.2-(30-)=41 B.+(41-)=30
C.+ =30 D.30-=41-
2.一项工程甲独做20天可以完成,乙独做30天可以完成.现在两个人合做,但是乙中途因事离开几天,从开工后14天把这项工作做完,则乙中途离开了( )
A.10天 B.9天 C.7天 D.5天
C
D
当堂训练
3.在某大型活动中,志愿者们手上、脖子上的丝巾非常美丽.车间70名工人承接了制作丝巾的任务,已知每人每天平均生产手上的丝巾1800条或者脖子上的丝巾1200条,一条脖子上的丝巾要配两条手上的丝巾.为了使每天生产的丝巾刚好配套,应分配多少名工人生产脖子上的丝巾,多少名工人生产手上的丝巾?
解:设应分配x名工人生产脖子上的丝巾,
分配(70-x)名工人生产手上的丝巾.
由题意得1800(70-x)=2×1200x,
解得x=30,则70-x=70-30=40.
答:应分配30名工人生产脖子上的丝巾,40名工人生产手上的丝巾.
当堂训练
4. 一件工作,甲单独做20小时完成,乙单独做12小时
完成,现在先由甲单独做4小时,剩下的部分由甲、
乙合做. 剩下的部分需要几小时完成?
解:设剩下的部分需要x小时完成,根据题意得:
解得x = 6.
答:剩下的部分需要6小时完成.
当堂训练
5. 一个道路工程,甲队单独施工9天完成,乙队单独
做24天完成.现在甲乙两队共同施工3天,因甲另
有任务,剩下的工程由乙队完成,问乙队还需几
天才能完成?
解:设乙队还需x天才能完成,由题意得:
解得 x = 13.
答:乙队还需13天才能完成.
课堂小结
肆
课堂小结
用一元一次方程解决实际问题的基本过程如下:
实际问题
设未知数,列方程
一元一次方程
实际问题的答案
解方程
一元一次方程的解
(x=a)
检验
课后作业
基础题:1.课后习题 第 2,5题。
提高题:2.课后习题 第 9,12题。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
