2.1 整式 第1课时 用字母表示数 课件(共31张PPT)
文档属性
| 名称 | 2.1 整式 第1课时 用字母表示数 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 21:38:39 | ||
图片预览







文档简介
(共31张PPT)
第1课时 用字母表示数
2.1 整 式
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
“一只青蛙一张嘴,两只眼睛,四条腿,一声扑通跳下水.两只青蛙两张嘴,四只眼睛,八条腿,两声扑通跳下水.”请接下去……
15只青蛙, 张嘴, 只眼睛, 条腿, 声扑通跳下水……
15
30
60
15
n只青蛙, 张嘴, 只眼睛, 条腿, 声扑通跳下水.
n
2n
4n
n
今天我们就学习用字母表示数.
讲授新知
贰
讲授新知
阅读教材P54~55内容,完成下列问题.
知识点1 含字母的式子的书写
用含有字母的式子表示下列数量
例1
(2)练习簿的单价为b 元, a本练习簿的总价是 元.
(1)练习簿的单价为a元,100本练习簿的总价是 元.
②字母和字母相乘,乘号可以省略不写或用“ · ” 表示.
一般情况下,按26个字母的顺序从左到右来写.
100a
ab
①数和字母相乘,可省略乘号,并把数字写在字母的前面
讲授新知
(3)练习簿的单价为0.5元,圆珠笔的单价是3.2元,
买a本练习簿和b支笔的总价是 元.
③后面带单位的相加或相减的式子要用括号括起来
(0.5a+3.2b)
④除法运算写成分数形式,即除号改为分数线
(4)小明的家离学校s千米,小明骑车上学.若每小时行
10千米,则需 时.
(5)若每斤苹果 元,则买m斤苹果需 元.
⑤带分数与字母相乘时,带分数要写成假分数的形式
讲授新知
(6)姚明个字高,经测量他通常跨一步的距离1米,
若取向前为正,向后为负,那么姚明向前跨
a步为 米,向后跨a步为 米.
a
-a
6.当“1”与任何字母相乘时,“1”省略不写;
当“-1”乘以字母时,只要在那个字母前加上“-”号.
1×a=a ; (-1)×a=-a
讲授新知
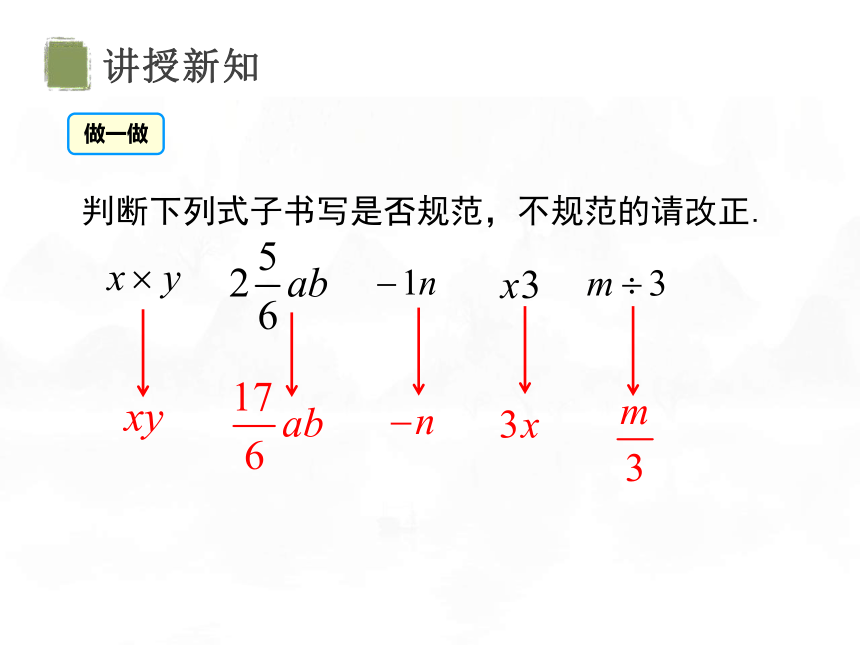
判断下列式子书写是否规范,不规范的请改正.
做一做
讲授新课
知识点2 用含字母的式子表示数量关系
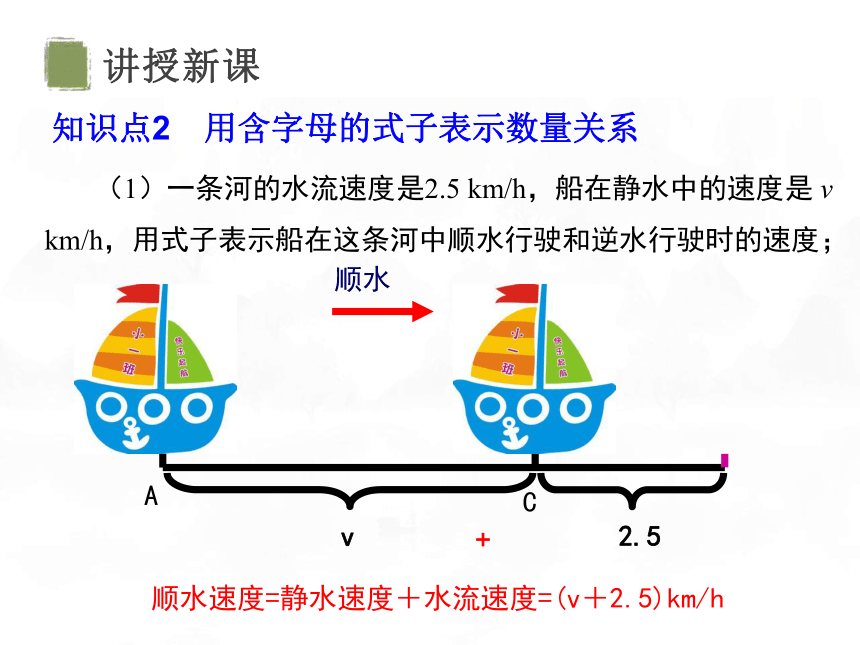
(1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
顺水
A
C
v
2.5
+
顺水速度=静水速度+水流速度=(v+2.5)km/h
讲授新课
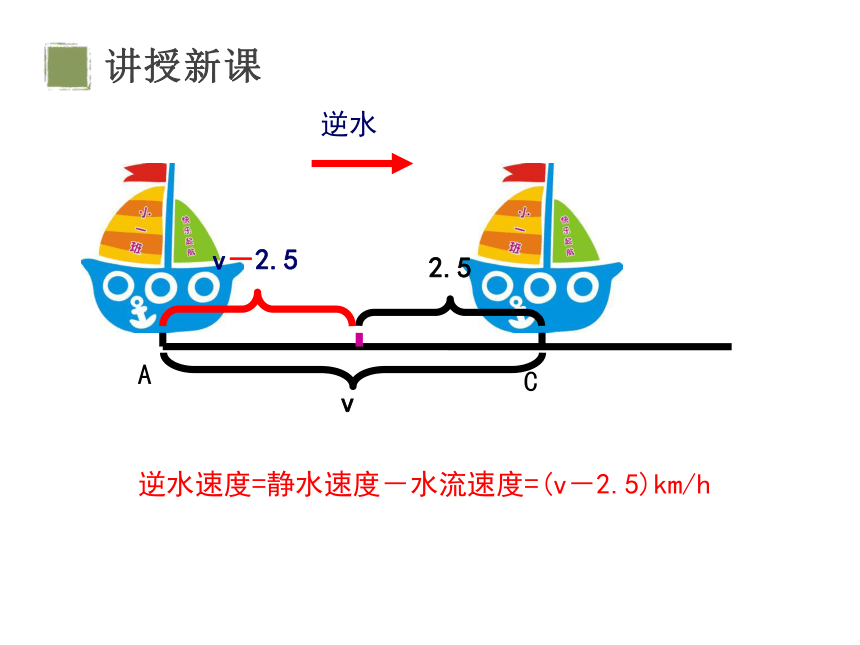
逆水
A
C
v
2.5
v-2.5
逆水速度=静水速度-水流速度=(v-2.5)km/h
讲授新课
(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数;
解:买3个篮球、5个排球、2个足球共需要3x+5y+2z元.
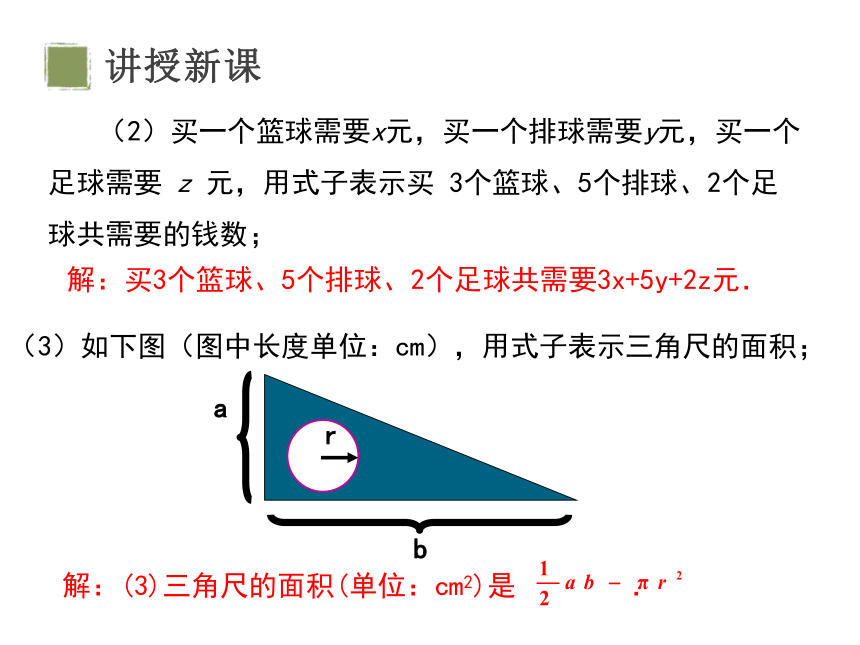
(3)如下图(图中长度单位:cm),用式子表示三角尺的面积;
解:(3)三角尺的面积(单位:cm2)是 .
a
b
r
讲授新课
(4)这所住宅的建筑面积(单位:m2) ( ).
(4)如下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
2
x
2x
x
x
x2
3
4
2
3
12
6
3
2
x
x
4
2
3
x
讲授新课
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
归纳:
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
讲授新课
用字母表示下列问题中的数量关系:
(1)为落实“阳光体育”工程,某校计划购买m个篮球和n个排球,已知篮球每个80元,排球每个60元,购买这些篮球和排球的总费用为 元.
(2)在运动会中,一班总成绩为m分,二班比一班总成绩的还多5分,则二班的总成绩为 .
(3)某商店压了一批商品,为尽快售出,该商店采取如下销售方案:将原来每件m元,加价50%,再做两次降价处理,第一次降价30%,第二次降价10%.经过两次降价后的价格为 元.
(80m+60n)
m+5
0.945m
讲授新课
知识点3 用字母表示规律
合作探究
如图所示,搭一个正方形需要4根火柴棒.
…
(1)按上面的方式,搭2个正方形需要____根火柴,
搭3个正方形需要____根火柴.
(2) 搭7个这样的正方形需要_____根火柴.
7
10
22
讲授新课
(3)搭100个这样的正方形需要多少根火柴
第1个
4根
第2个
第100个
3根
3根
…
有没有其他计算方法?
讲授新课
先摆 1根
第1个
3根
第100个
…
第2个
3根
3根
还可以这样
讲授新课
(4) 如果用 x 表示所搭正方形的个数, 那么搭 x 个
这样的正方形需要多少根火柴
第1个
4根
第2个
第100个
3根
3根
…
讲授新课
先摆 1根
第1个
3根
第100个
…
第2个
3根
3根
或者这样
范例应用
例3 观察下列图形:
它们是按一定规律排列的.
(1)依照此规律,第20个图形共有几个五角星?
(2)摆成第n个图案需要几个五角星?
(3)摆成第2022个图案需要几个五角星?
范例应用
解:(1)根据题意得∵第1个图中,五角星有3个(3×1);第2个图中,有五角星6个(3×2);第3个图中,有五角星9个(3×3);第4个图中,有五角星12个(3×4);∴第n个图中有五角星3n个.∴第20个图中五角星有3×20=60个.
(2)由(1)可知,摆成第n个图案需要3n个五角星.
(3)摆成第2022个图案需要五角星2022×3=6066(个).
当堂训练
叁
当堂训练
1.下列各式符合书写要求的是( )
A.1a B.n·2 C.a÷b D.2πr2
2.在下列表述中,不能表示“4a”的意义的是( )
A.4与a的积 B.a的4倍C.4个a相加 D.4个a相乘
3.a的平方与b的和,用式子表示,正确的是( )
A.a+b2 B.a2+bC.a2+b2 D.(a+b)2
4.长春市净月潭国家森林公园门票的价格为成人票每张30元,儿童票每张15元.若购买m张成人票和n张儿童票,则共需花费 元.
D
D
B
(30m+15n)
当堂训练
5.如图,用火柴棍拼成一个由三角形组成的图形,拼第一个图形共需要3根火柴棍;拼第二个图形共需要5根火柴棍;拼第三个图形共需要7根火柴棍;…照这样拼图,则第n个图形需要 根火柴棍.
(2n+1)
课堂小结
肆
课堂小结
壹
用字母表示数
用式子把数量关系简明地表示出来
列式的注意事项
数与字母、字母和字母相乘省略乘号
数与字母相乘时数字写在前面
探究图形的变化规律
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.课后习题 第 7,8题。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第1课时 用字母表示数
2.1 整 式
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
“一只青蛙一张嘴,两只眼睛,四条腿,一声扑通跳下水.两只青蛙两张嘴,四只眼睛,八条腿,两声扑通跳下水.”请接下去……
15只青蛙, 张嘴, 只眼睛, 条腿, 声扑通跳下水……
15
30
60
15
n只青蛙, 张嘴, 只眼睛, 条腿, 声扑通跳下水.
n
2n
4n
n
今天我们就学习用字母表示数.
讲授新知
贰
讲授新知
阅读教材P54~55内容,完成下列问题.
知识点1 含字母的式子的书写
用含有字母的式子表示下列数量
例1
(2)练习簿的单价为b 元, a本练习簿的总价是 元.
(1)练习簿的单价为a元,100本练习簿的总价是 元.
②字母和字母相乘,乘号可以省略不写或用“ · ” 表示.
一般情况下,按26个字母的顺序从左到右来写.
100a
ab
①数和字母相乘,可省略乘号,并把数字写在字母的前面
讲授新知
(3)练习簿的单价为0.5元,圆珠笔的单价是3.2元,
买a本练习簿和b支笔的总价是 元.
③后面带单位的相加或相减的式子要用括号括起来
(0.5a+3.2b)
④除法运算写成分数形式,即除号改为分数线
(4)小明的家离学校s千米,小明骑车上学.若每小时行
10千米,则需 时.
(5)若每斤苹果 元,则买m斤苹果需 元.
⑤带分数与字母相乘时,带分数要写成假分数的形式
讲授新知
(6)姚明个字高,经测量他通常跨一步的距离1米,
若取向前为正,向后为负,那么姚明向前跨
a步为 米,向后跨a步为 米.
a
-a
6.当“1”与任何字母相乘时,“1”省略不写;
当“-1”乘以字母时,只要在那个字母前加上“-”号.
1×a=a ; (-1)×a=-a
讲授新知
判断下列式子书写是否规范,不规范的请改正.
做一做
讲授新课
知识点2 用含字母的式子表示数量关系
(1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
顺水
A
C
v
2.5
+
顺水速度=静水速度+水流速度=(v+2.5)km/h
讲授新课
逆水
A
C
v
2.5
v-2.5
逆水速度=静水速度-水流速度=(v-2.5)km/h
讲授新课
(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数;
解:买3个篮球、5个排球、2个足球共需要3x+5y+2z元.
(3)如下图(图中长度单位:cm),用式子表示三角尺的面积;
解:(3)三角尺的面积(单位:cm2)是 .
a
b
r
讲授新课
(4)这所住宅的建筑面积(单位:m2) ( ).
(4)如下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
2
x
2x
x
x
x2
3
4
2
3
12
6
3
2
x
x
4
2
3
x
讲授新课
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
归纳:
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
讲授新课
用字母表示下列问题中的数量关系:
(1)为落实“阳光体育”工程,某校计划购买m个篮球和n个排球,已知篮球每个80元,排球每个60元,购买这些篮球和排球的总费用为 元.
(2)在运动会中,一班总成绩为m分,二班比一班总成绩的还多5分,则二班的总成绩为 .
(3)某商店压了一批商品,为尽快售出,该商店采取如下销售方案:将原来每件m元,加价50%,再做两次降价处理,第一次降价30%,第二次降价10%.经过两次降价后的价格为 元.
(80m+60n)
m+5
0.945m
讲授新课
知识点3 用字母表示规律
合作探究
如图所示,搭一个正方形需要4根火柴棒.
…
(1)按上面的方式,搭2个正方形需要____根火柴,
搭3个正方形需要____根火柴.
(2) 搭7个这样的正方形需要_____根火柴.
7
10
22
讲授新课
(3)搭100个这样的正方形需要多少根火柴
第1个
4根
第2个
第100个
3根
3根
…
有没有其他计算方法?
讲授新课
先摆 1根
第1个
3根
第100个
…
第2个
3根
3根
还可以这样
讲授新课
(4) 如果用 x 表示所搭正方形的个数, 那么搭 x 个
这样的正方形需要多少根火柴
第1个
4根
第2个
第100个
3根
3根
…
讲授新课
先摆 1根
第1个
3根
第100个
…
第2个
3根
3根
或者这样
范例应用
例3 观察下列图形:
它们是按一定规律排列的.
(1)依照此规律,第20个图形共有几个五角星?
(2)摆成第n个图案需要几个五角星?
(3)摆成第2022个图案需要几个五角星?
范例应用
解:(1)根据题意得∵第1个图中,五角星有3个(3×1);第2个图中,有五角星6个(3×2);第3个图中,有五角星9个(3×3);第4个图中,有五角星12个(3×4);∴第n个图中有五角星3n个.∴第20个图中五角星有3×20=60个.
(2)由(1)可知,摆成第n个图案需要3n个五角星.
(3)摆成第2022个图案需要五角星2022×3=6066(个).
当堂训练
叁
当堂训练
1.下列各式符合书写要求的是( )
A.1a B.n·2 C.a÷b D.2πr2
2.在下列表述中,不能表示“4a”的意义的是( )
A.4与a的积 B.a的4倍C.4个a相加 D.4个a相乘
3.a的平方与b的和,用式子表示,正确的是( )
A.a+b2 B.a2+bC.a2+b2 D.(a+b)2
4.长春市净月潭国家森林公园门票的价格为成人票每张30元,儿童票每张15元.若购买m张成人票和n张儿童票,则共需花费 元.
D
D
B
(30m+15n)
当堂训练
5.如图,用火柴棍拼成一个由三角形组成的图形,拼第一个图形共需要3根火柴棍;拼第二个图形共需要5根火柴棍;拼第三个图形共需要7根火柴棍;…照这样拼图,则第n个图形需要 根火柴棍.
(2n+1)
课堂小结
肆
课堂小结
壹
用字母表示数
用式子把数量关系简明地表示出来
列式的注意事项
数与字母、字母和字母相乘省略乘号
数与字母相乘时数字写在前面
探究图形的变化规律
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.课后习题 第 7,8题。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
