2.2 整式的加减 第1课时 合并同类项 课件(共32张PPT)
文档属性
| 名称 | 2.2 整式的加减 第1课时 合并同类项 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
第1课时 合并同类项
2.2 整式的加减
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
周末,你和爸爸妈妈要外出游玩,中午决定在外面用餐,爸爸、妈妈和你各自选了要吃的东西,爸爸选了一个汉堡和一杯可乐,妈妈选了一个汉堡和一个冰淇淋,你选了一对蛋挞和一杯可乐,买的时候你该怎么向服务员点餐?生活中处处有数学的存在.可以把具有相同特征的事物归为一类,在多项式中也可以把具有相同特征的单项式归为一类.
讲授新知
贰
讲授新知
阅读教材P62~64内容,完成下列问题.
知识点1 同类项的辨别
8n
-7a2b
3ab2
2a2b
6xy
5n
-3xy
-ab2
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里吗?(无论你用几个房间)
讲授新知
8n
-7a2b
3ab2
2a2b
6xy
5n
-3xy
-ab2
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里吗?(无论你用几个房间)
讲授新知
8n 5n
3ab2 -ab2
6xy -3xy
-7a2b 2a2b
n
n
xy
xy
a b
a b
ab
ab
2
2
2
2
我们把具有以上两个特征的单项式称为同类项
1.所含字母相同
2.相同字母指数也相同
相同
所有的常数项也看做同类项
相同
知识要点
范例应用
例1 先判断每一组是否是同类项,不是的,为前者配一个.
(1)2x2y与-3x2y;(2)2abc与2ab;
(3)-3pq与3qp;(4)-4x2y与5xy2.
解:(1)是. (2)不是.2abc的一个同类项为abc.(3)是.(4)不是.-4x y的一个同类项为x y.
【方法归纳】
同类项的“两相同”和“两无关”
(1)“两相同”:一是所含字母相同,二是相同字母的指数也分别相同.这“两相同”同时也是判断同类项的标准,两者缺一不可.
(2)“两无关”:一是与系数的大小无关;二是与所含字母的顺序无关.
范例应用
【练习】
1.下面不是同类项的是( )
A.2m与2n B.-2a2b与ba2
C.-x2y2与6x2y2 D.-2与5
2.如果单项式3xmy与-5x3yn是同类项,那么m+n= .
A
4
讲授新课
知识点2 合并同类项及应用
周末,小明一家要外出游玩,爸爸、妈妈和小明各自选了他们要吃的东西:
买的时候,小明怎么说?
____个面包____个苹果____个草莓_____瓶饮料
4 3 8 3
2个面包+1个面包+1个面包= 个面包
2个草莓+3个草莓+3个草莓= 个草莓
4
8
讲授新课
x
x
x
2
+3
=
5
=
3
-
a2bc
a2bc
a2bc
2
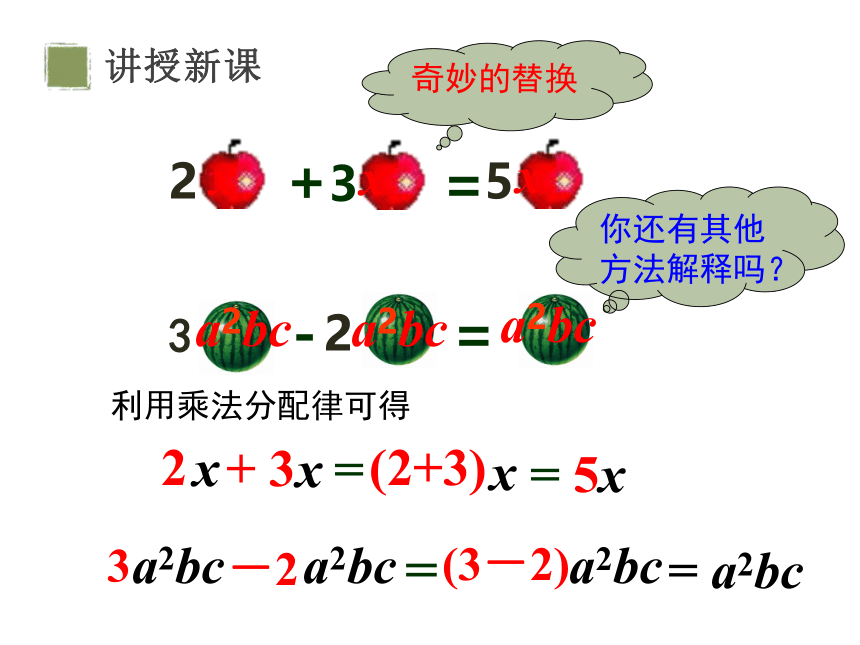
奇妙的替换
你还有其他方法解释吗?
利用乘法分配律可得
(2+3)
x
x
2
+ 3
=
x
=
3
a2bc
a2bc
a2bc
-2
(3-2)
= 5x
= a2bc
讲授新课
2.合并同类项的法则:
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
1.把多项式中的同类项合并成一项叫做合并同类项.
知识要点
3 ab + 5 ab = 8 ab
相加
不变
范例应用
例2 下列合并同类项对吗?不对的,说明理由.
(1)a+a=2a
(2)3a+2b=5ab
(3)5y2-3y2=2
(4)4x2y-5xy2=-x2y
(5)3x2+2x3=5x5
(6)a+a-5a=-3a
×
√
×
×
×
√
注:(2)(4)(5)中的单项式不是同类项,不能合并
范例应用
例2. 合并下式中的同类项.
解:
找
移
并
用不同的标记把同类项标出来!
加法交换律加法结合律
范例应用
【练习】
将下列各式合并同类项.
(1)-x-x-x;
(2)2a2-3ab+4b2-5ab-6b2;
解:(1)-x-x-x
=(-1-1-1)x
=-3x;
(2)2a2-3ab+4b2-5ab-6b2
=2a2+(4-6)b2+(-3-5)ab
=2a2-2b2-8ab.
范例应用
【方法归纳】
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三合,将同一括号内的同类项相加即可.
范例应用
例3 化简求值:2a2b-2ab+3-3a2b+4ab,
其中a=-2,b= .
解:2a2b-2ab+3-3a2b+4ab
=(2-3)a2b+(-2+4)ab+3
=-a2b+2ab+3.
将a=-2,b= 代入得
原式=-(-2)2× +2×(-2)× +3
=-1.
范例应用
【方法归纳】
对多项式化简求值时,一般先化简,即先合并同类项,再代入值计算结果,在算式中代入负数时,要注意添加负号.
范例应用
【练习】
先合并同类项,再求式子的值:
范例应用
例4 一天,王村的小明奶奶提着一篮子土豆去换苹果,双方商定的结果是:1千克土豆换0.5千克苹果.当称完带篮子的土豆重量后,摊主对小明奶奶说:“别称篮子的重量了,称苹果时也带篮子称,这样既省事又互不吃亏.”你认为摊主的话有道理吗?请你用所学的有关数学知识加以判定.
解:设土豆重a千克,篮子重b千克,则应换苹果0.5a千克.若不称篮子,则实换苹果为0.5a+0.5b-b=(0.5a-0.5b)千克,很明显小明奶奶少得苹果0.5b千克.所以摊主说得没有道理,这样做小明奶奶吃亏了.
范例应用
【练习】
有一批货物,甲可以3天运完,乙可以6天运完,若共有x吨货物,甲乙合作运输一天后还有多少吨没有运完?
当堂训练
叁
当堂训练
1.下列各组式子中是同类项的是( )
A.-2a与a2 B.2a2b与3ab2
C.5ab2c与-b2ac D.-ab2和4ab2c
2.下列运算中,正确的是( )
A.2a+3b=5ab B.3a2-2a2=1
C.4a2b-3ba2=a2b D.-a-2a-3a=0
3.如果单项式3xmy与-5x3yn是同类项,那么m+n= .
C
C
4
当堂训练
4.如右图,左边三角形的面积为2m2-3m,右边三角形的面积为9+5m,空白部分的面积为m2,则图中阴影部分的面积为 .
2m+9
5.合并下列各式中的同类项:
(1)3a2-2a+4a2-7a;
(2)- mn+5mn2-1+ mn-5n2m+1.
解:(1)原式=7a2-9a.
(2)原式=- mn.
当堂训练
6.小明用3天看完一本课外读物,第一天看了a页,第二天看的比第一天多50页,第三天看的比第二天少85页.
(1)用含a的式子表示这本书的页数;
(2)当a=50时,这本书的页数是多少?
解:(1)这本书的页数为a+a+50+a+50-85
=3a+15.
(2)当a=50时,3a+15=3×50+15=165.
答:当a=50时,这本书的页数是165.
课堂小结
肆
课堂小结
壹
同类项
两同
两无关
与系数无关
与所含字母的顺序无关
合并同类项
“一加二不变”
所含字母相同
相同字母的指数相同
课后作业
基础题:1.课后练习题 第 1,2,3题。
提高题:2.有这样的一道题:“当x= ,y=2022时,求多项式7x3-6x3y+3x2y+3x3+6x3y-3x2y-10x3+3的值.”小聪同学说题目中给出的条件“x= ,y=2022”是多余的,他的说法有道理吗?为什么?
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第1课时 合并同类项
2.2 整式的加减
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
周末,你和爸爸妈妈要外出游玩,中午决定在外面用餐,爸爸、妈妈和你各自选了要吃的东西,爸爸选了一个汉堡和一杯可乐,妈妈选了一个汉堡和一个冰淇淋,你选了一对蛋挞和一杯可乐,买的时候你该怎么向服务员点餐?生活中处处有数学的存在.可以把具有相同特征的事物归为一类,在多项式中也可以把具有相同特征的单项式归为一类.
讲授新知
贰
讲授新知
阅读教材P62~64内容,完成下列问题.
知识点1 同类项的辨别
8n
-7a2b
3ab2
2a2b
6xy
5n
-3xy
-ab2
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里吗?(无论你用几个房间)
讲授新知
8n
-7a2b
3ab2
2a2b
6xy
5n
-3xy
-ab2
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里吗?(无论你用几个房间)
讲授新知
8n 5n
3ab2 -ab2
6xy -3xy
-7a2b 2a2b
n
n
xy
xy
a b
a b
ab
ab
2
2
2
2
我们把具有以上两个特征的单项式称为同类项
1.所含字母相同
2.相同字母指数也相同
相同
所有的常数项也看做同类项
相同
知识要点
范例应用
例1 先判断每一组是否是同类项,不是的,为前者配一个.
(1)2x2y与-3x2y;(2)2abc与2ab;
(3)-3pq与3qp;(4)-4x2y与5xy2.
解:(1)是. (2)不是.2abc的一个同类项为abc.(3)是.(4)不是.-4x y的一个同类项为x y.
【方法归纳】
同类项的“两相同”和“两无关”
(1)“两相同”:一是所含字母相同,二是相同字母的指数也分别相同.这“两相同”同时也是判断同类项的标准,两者缺一不可.
(2)“两无关”:一是与系数的大小无关;二是与所含字母的顺序无关.
范例应用
【练习】
1.下面不是同类项的是( )
A.2m与2n B.-2a2b与ba2
C.-x2y2与6x2y2 D.-2与5
2.如果单项式3xmy与-5x3yn是同类项,那么m+n= .
A
4
讲授新课
知识点2 合并同类项及应用
周末,小明一家要外出游玩,爸爸、妈妈和小明各自选了他们要吃的东西:
买的时候,小明怎么说?
____个面包____个苹果____个草莓_____瓶饮料
4 3 8 3
2个面包+1个面包+1个面包= 个面包
2个草莓+3个草莓+3个草莓= 个草莓
4
8
讲授新课
x
x
x
2
+3
=
5
=
3
-
a2bc
a2bc
a2bc
2
奇妙的替换
你还有其他方法解释吗?
利用乘法分配律可得
(2+3)
x
x
2
+ 3
=
x
=
3
a2bc
a2bc
a2bc
-2
(3-2)
= 5x
= a2bc
讲授新课
2.合并同类项的法则:
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
1.把多项式中的同类项合并成一项叫做合并同类项.
知识要点
3 ab + 5 ab = 8 ab
相加
不变
范例应用
例2 下列合并同类项对吗?不对的,说明理由.
(1)a+a=2a
(2)3a+2b=5ab
(3)5y2-3y2=2
(4)4x2y-5xy2=-x2y
(5)3x2+2x3=5x5
(6)a+a-5a=-3a
×
√
×
×
×
√
注:(2)(4)(5)中的单项式不是同类项,不能合并
范例应用
例2. 合并下式中的同类项.
解:
找
移
并
用不同的标记把同类项标出来!
加法交换律加法结合律
范例应用
【练习】
将下列各式合并同类项.
(1)-x-x-x;
(2)2a2-3ab+4b2-5ab-6b2;
解:(1)-x-x-x
=(-1-1-1)x
=-3x;
(2)2a2-3ab+4b2-5ab-6b2
=2a2+(4-6)b2+(-3-5)ab
=2a2-2b2-8ab.
范例应用
【方法归纳】
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三合,将同一括号内的同类项相加即可.
范例应用
例3 化简求值:2a2b-2ab+3-3a2b+4ab,
其中a=-2,b= .
解:2a2b-2ab+3-3a2b+4ab
=(2-3)a2b+(-2+4)ab+3
=-a2b+2ab+3.
将a=-2,b= 代入得
原式=-(-2)2× +2×(-2)× +3
=-1.
范例应用
【方法归纳】
对多项式化简求值时,一般先化简,即先合并同类项,再代入值计算结果,在算式中代入负数时,要注意添加负号.
范例应用
【练习】
先合并同类项,再求式子的值:
范例应用
例4 一天,王村的小明奶奶提着一篮子土豆去换苹果,双方商定的结果是:1千克土豆换0.5千克苹果.当称完带篮子的土豆重量后,摊主对小明奶奶说:“别称篮子的重量了,称苹果时也带篮子称,这样既省事又互不吃亏.”你认为摊主的话有道理吗?请你用所学的有关数学知识加以判定.
解:设土豆重a千克,篮子重b千克,则应换苹果0.5a千克.若不称篮子,则实换苹果为0.5a+0.5b-b=(0.5a-0.5b)千克,很明显小明奶奶少得苹果0.5b千克.所以摊主说得没有道理,这样做小明奶奶吃亏了.
范例应用
【练习】
有一批货物,甲可以3天运完,乙可以6天运完,若共有x吨货物,甲乙合作运输一天后还有多少吨没有运完?
当堂训练
叁
当堂训练
1.下列各组式子中是同类项的是( )
A.-2a与a2 B.2a2b与3ab2
C.5ab2c与-b2ac D.-ab2和4ab2c
2.下列运算中,正确的是( )
A.2a+3b=5ab B.3a2-2a2=1
C.4a2b-3ba2=a2b D.-a-2a-3a=0
3.如果单项式3xmy与-5x3yn是同类项,那么m+n= .
C
C
4
当堂训练
4.如右图,左边三角形的面积为2m2-3m,右边三角形的面积为9+5m,空白部分的面积为m2,则图中阴影部分的面积为 .
2m+9
5.合并下列各式中的同类项:
(1)3a2-2a+4a2-7a;
(2)- mn+5mn2-1+ mn-5n2m+1.
解:(1)原式=7a2-9a.
(2)原式=- mn.
当堂训练
6.小明用3天看完一本课外读物,第一天看了a页,第二天看的比第一天多50页,第三天看的比第二天少85页.
(1)用含a的式子表示这本书的页数;
(2)当a=50时,这本书的页数是多少?
解:(1)这本书的页数为a+a+50+a+50-85
=3a+15.
(2)当a=50时,3a+15=3×50+15=165.
答:当a=50时,这本书的页数是165.
课堂小结
肆
课堂小结
壹
同类项
两同
两无关
与系数无关
与所含字母的顺序无关
合并同类项
“一加二不变”
所含字母相同
相同字母的指数相同
课后作业
基础题:1.课后练习题 第 1,2,3题。
提高题:2.有这样的一道题:“当x= ,y=2022时,求多项式7x3-6x3y+3x2y+3x3+6x3y-3x2y-10x3+3的值.”小聪同学说题目中给出的条件“x= ,y=2022”是多余的,他的说法有道理吗?为什么?
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
