1.2.3 相反数 课件(共26张PPT)
文档属性
| 名称 | 1.2.3 相反数 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
1.2.3 相反数
1.2 有理数
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
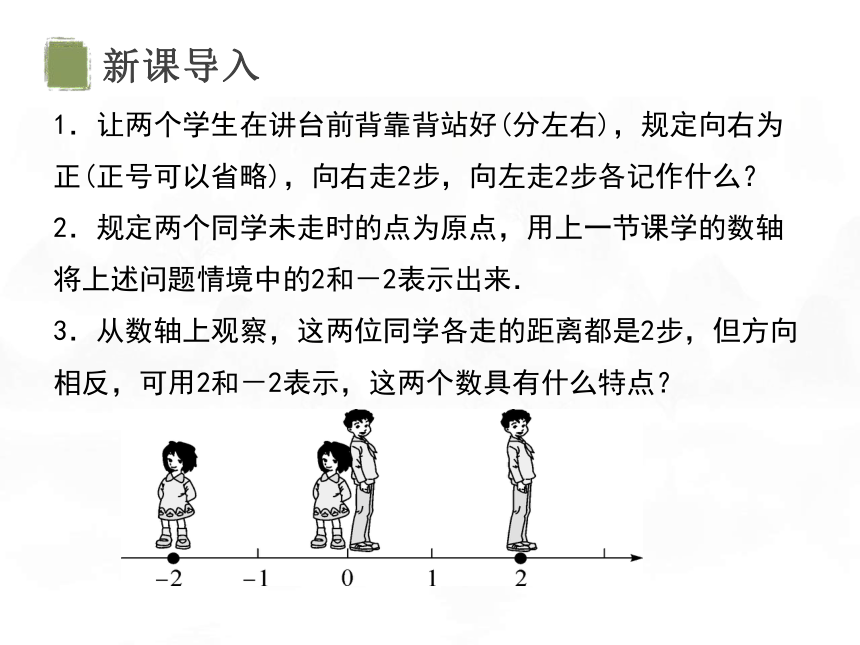
1.让两个学生在讲台前背靠背站好(分左右),规定向右为正(正号可以省略),向右走2步,向左走2步各记作什么?
2.规定两个同学未走时的点为原点,用上一节课学的数轴将上述问题情境中的2和-2表示出来.
3.从数轴上观察,这两位同学各走的距离都是2步,但方向相反,可用2和-2表示,这两个数具有什么特点?
讲授新知
贰
讲授新知
活动1:观察下列一组数+1和-1,+2.5和-2.5,+4和-4,并把它们在数轴上表示出来.
阅读教材P9~10内容,完成下列问题.
知识点1 相反数的概念
思考:
(1)上述各对数之间有什么特点?
(2)请写出一组具有上述特点的数
(3)你能得出相反数的概念吗?
(4)表示各对数的点在数轴上有什么位置关系?
1.只有符号不同的两个数叫做互为相反数.
2.一般地,a和-a互为相反数.
讲授新知
自主归纳
相反数的定义
例1 判断题:
(1)-5是5的相反数;( )
(2)-5是相反数;( )
(3) 与 互为相反数;( )
(4)-5和5互为相反数;( )
(5) 相反数等于它本身的数只有0; ﹙ ﹚
(6) 符号不同的两个数互为相反数.﹙ ﹚
×
√
×
√
√
×
范例应用
【方法归纳】
正数的相反数是负数,负数的相反数是正数
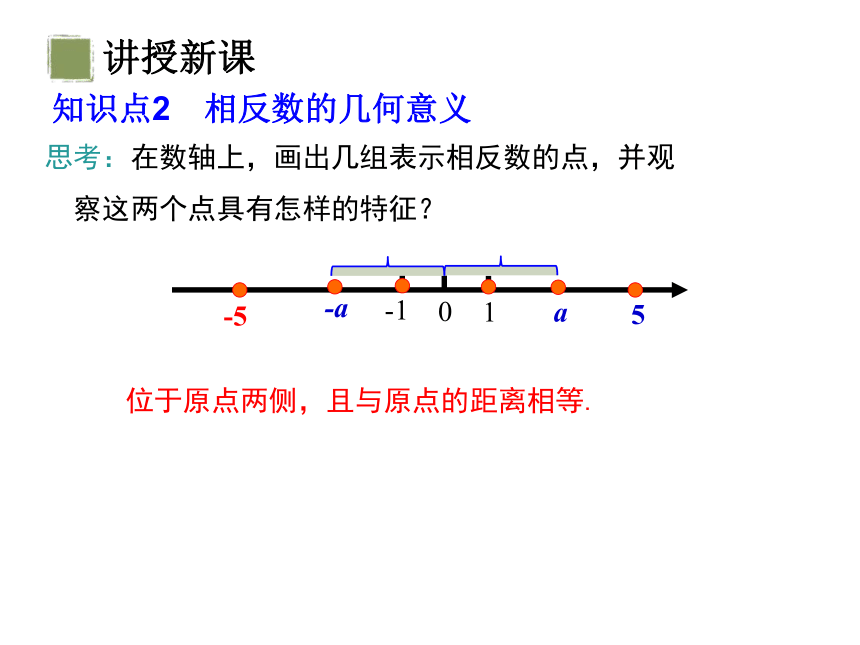
思考:在数轴上,画出几组表示相反数的点,并观
察这两个点具有怎样的特征?
位于原点两侧,且与原点的距离相等.
0
5
-5
-1
1
a
-a
讲授新课
知识点2 相反数的几何意义
问题2:数轴上到原点的距离相等的点所表示的数有什
么特点?借助数轴填一填:
1.数轴上与原点距离是2的点有____个,这些点表示的
数是________;
2.与原点的距离是5的点有____个,这些点表示的数是
________.
0
2
-2
两
2和-2
5和-5
两
5
-5
讲授新课
讲授新课
1.互为相反数的两个数分别位于原点的两侧(0除外).
2.互为相反数的两个数到原点的距离相等.
3.一般地,设a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点的两侧,表示a和-a,这两点关于原点对称.
要点归纳
范例应用
例2 填空:
(1)数轴上离原点3个单位长度的点所表示的数是 ,它们的关系为互为 .
(2)在数轴上,若点A和点B分别表示互为相反数的两个数,点A在点B的左侧,并且这两个数的距离是12.8,
则A= ,B= .
3和-3
相反数
-6.4
6.4
范例应用
例3 如图,图中数轴(缺原点)的单位长度为1,点A、B表示的两数互为相反数,则点C所表示的数为( )
C
A.2 B.-4 C.-1 D.0
点拨:由题意如图,
数轴向右为正方向,数轴(缺原点)的单位长度为1,∴点C所表示的数为-1,故应选C.
【方法归纳】先在数轴上找到原点,从而确定点C所表示的数,同时牢记互为相反数的两个点到原点的距离相等.
讲授新课
知识点3 多重符号的化简
问题1:a的相反数是什么?如何求一个数的相反数?
a的相反数是-a,在这个数前加一个“-”号.
问题2:若把a分别换成+5,-7,0时,这些数的相反数怎样表示?
a=+5,-a=-(+5);a=-7,-a=-(-7);a=0,-a=0.
讲授新课
-(+1.1)表示什么?-(-7)呢?-(-9.8)呢?它们的结果应是多少?
-(+1.1)表示1.1的相反数;-(-7)表示-7的相反数;-(-9.8)表示-9.8的相反数.它们的结果分别是-1.1,7,9.8.
问题3:在一个数前面加上“-”号表示求这个数的相反数,如果在这些数前面加上“+”号呢?
表示它本身
范例应用
例4 填空
(1)-(+4)是 的相反数,-(+4)= .
(2) 是 的相反数, = .
(3) -(-7.1)是 的相反数,-(-7.1)= .
+4
-4
-7.1
7.1
【方法归纳】求一个数的相反数,只要在这个数的前面添上“-”号,就表示这个数的相反数.
化简下列各数(先读后写)
(1)-(+10) (2)+(-0.15) (3)+(+3)
(4)-(-12) (5)+[-(-1.1)] (6)-[+(-7)]
例5
(6)-[+(-7)]=-(-7)=7.
由内向外依次去括号
【方法归纳】化简多重符号时,只需数一下数字前面有多少个负号,若有偶数个,则结果为正;若有奇数个,则结果为负.
解:(1)-(+10)=-10;
(2)+(-0.15)=-0.15;
(3)+(+3)=3;
(4)-(-12)=12;
(5)+[-(-1.1)]=+(+1.1)=1.1;
范例应用
当堂训练
叁
当堂训练
1.9的相反数是( )
A.-9或9 B.- C.9 D.-9
2.下列结论正确的有( )
①任何数都不等于它的相反数;②符号相反的数互为相反数;③表示互为相反数的两个数的点到原点的距离相等;④若有理数a,b互为相反数,则它们一定异号.
A.1个 B.2个 C.3个 D.4个
D
A
3.下列几对数中不是互为相反数的一对为( )
A.-(-8)和-(+8) B.+(+8)和-(+8)
C.+(-8)和+(+8) D.-(+8)和+(-8)
D
当堂训练
4.填一填
(1)-1.6是 的相反数, 的相反数是0.3.
a的相反数是 ;
(2)若a=-13,则-a= ;若-a=-6,则a= .
(3)若a是负数,则-a是 数;若-a是负数,
则a是 数.
(4) 的相反数是 ,-3x的相反数是 .
5.已知数轴上A、B表示的数互为相反数,并且两点间的距离是6,点A在点B的左边,则点A、B表示的数分别是 .
1.6
-0.3
-a
13
6
正
正
3x
-3,3
课堂小结
肆
课堂小结
壹
相反数
定义
只有符号不同的两个数.
性质
a的相反数是-a,0的相反数是0.
互为相反数的两个数到原点的距离相等.
多重符号的化简
偶数个“-”号,结果为正数.
奇数个“-”号,结果为负数.
课后作业
基础题:1.课后习题 第 4题。
提高题:2.如图,在一条不完整的数轴上,动点A向左移动4个单位长度到达点B,再向右移动7个单位长度到达点C.如果点A、C表示的数互为相反数,求点B表示的数.
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.2.3 相反数
1.2 有理数
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
1.让两个学生在讲台前背靠背站好(分左右),规定向右为正(正号可以省略),向右走2步,向左走2步各记作什么?
2.规定两个同学未走时的点为原点,用上一节课学的数轴将上述问题情境中的2和-2表示出来.
3.从数轴上观察,这两位同学各走的距离都是2步,但方向相反,可用2和-2表示,这两个数具有什么特点?
讲授新知
贰
讲授新知
活动1:观察下列一组数+1和-1,+2.5和-2.5,+4和-4,并把它们在数轴上表示出来.
阅读教材P9~10内容,完成下列问题.
知识点1 相反数的概念
思考:
(1)上述各对数之间有什么特点?
(2)请写出一组具有上述特点的数
(3)你能得出相反数的概念吗?
(4)表示各对数的点在数轴上有什么位置关系?
1.只有符号不同的两个数叫做互为相反数.
2.一般地,a和-a互为相反数.
讲授新知
自主归纳
相反数的定义
例1 判断题:
(1)-5是5的相反数;( )
(2)-5是相反数;( )
(3) 与 互为相反数;( )
(4)-5和5互为相反数;( )
(5) 相反数等于它本身的数只有0; ﹙ ﹚
(6) 符号不同的两个数互为相反数.﹙ ﹚
×
√
×
√
√
×
范例应用
【方法归纳】
正数的相反数是负数,负数的相反数是正数
思考:在数轴上,画出几组表示相反数的点,并观
察这两个点具有怎样的特征?
位于原点两侧,且与原点的距离相等.
0
5
-5
-1
1
a
-a
讲授新课
知识点2 相反数的几何意义
问题2:数轴上到原点的距离相等的点所表示的数有什
么特点?借助数轴填一填:
1.数轴上与原点距离是2的点有____个,这些点表示的
数是________;
2.与原点的距离是5的点有____个,这些点表示的数是
________.
0
2
-2
两
2和-2
5和-5
两
5
-5
讲授新课
讲授新课
1.互为相反数的两个数分别位于原点的两侧(0除外).
2.互为相反数的两个数到原点的距离相等.
3.一般地,设a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点的两侧,表示a和-a,这两点关于原点对称.
要点归纳
范例应用
例2 填空:
(1)数轴上离原点3个单位长度的点所表示的数是 ,它们的关系为互为 .
(2)在数轴上,若点A和点B分别表示互为相反数的两个数,点A在点B的左侧,并且这两个数的距离是12.8,
则A= ,B= .
3和-3
相反数
-6.4
6.4
范例应用
例3 如图,图中数轴(缺原点)的单位长度为1,点A、B表示的两数互为相反数,则点C所表示的数为( )
C
A.2 B.-4 C.-1 D.0
点拨:由题意如图,
数轴向右为正方向,数轴(缺原点)的单位长度为1,∴点C所表示的数为-1,故应选C.
【方法归纳】先在数轴上找到原点,从而确定点C所表示的数,同时牢记互为相反数的两个点到原点的距离相等.
讲授新课
知识点3 多重符号的化简
问题1:a的相反数是什么?如何求一个数的相反数?
a的相反数是-a,在这个数前加一个“-”号.
问题2:若把a分别换成+5,-7,0时,这些数的相反数怎样表示?
a=+5,-a=-(+5);a=-7,-a=-(-7);a=0,-a=0.
讲授新课
-(+1.1)表示什么?-(-7)呢?-(-9.8)呢?它们的结果应是多少?
-(+1.1)表示1.1的相反数;-(-7)表示-7的相反数;-(-9.8)表示-9.8的相反数.它们的结果分别是-1.1,7,9.8.
问题3:在一个数前面加上“-”号表示求这个数的相反数,如果在这些数前面加上“+”号呢?
表示它本身
范例应用
例4 填空
(1)-(+4)是 的相反数,-(+4)= .
(2) 是 的相反数, = .
(3) -(-7.1)是 的相反数,-(-7.1)= .
+4
-4
-7.1
7.1
【方法归纳】求一个数的相反数,只要在这个数的前面添上“-”号,就表示这个数的相反数.
化简下列各数(先读后写)
(1)-(+10) (2)+(-0.15) (3)+(+3)
(4)-(-12) (5)+[-(-1.1)] (6)-[+(-7)]
例5
(6)-[+(-7)]=-(-7)=7.
由内向外依次去括号
【方法归纳】化简多重符号时,只需数一下数字前面有多少个负号,若有偶数个,则结果为正;若有奇数个,则结果为负.
解:(1)-(+10)=-10;
(2)+(-0.15)=-0.15;
(3)+(+3)=3;
(4)-(-12)=12;
(5)+[-(-1.1)]=+(+1.1)=1.1;
范例应用
当堂训练
叁
当堂训练
1.9的相反数是( )
A.-9或9 B.- C.9 D.-9
2.下列结论正确的有( )
①任何数都不等于它的相反数;②符号相反的数互为相反数;③表示互为相反数的两个数的点到原点的距离相等;④若有理数a,b互为相反数,则它们一定异号.
A.1个 B.2个 C.3个 D.4个
D
A
3.下列几对数中不是互为相反数的一对为( )
A.-(-8)和-(+8) B.+(+8)和-(+8)
C.+(-8)和+(+8) D.-(+8)和+(-8)
D
当堂训练
4.填一填
(1)-1.6是 的相反数, 的相反数是0.3.
a的相反数是 ;
(2)若a=-13,则-a= ;若-a=-6,则a= .
(3)若a是负数,则-a是 数;若-a是负数,
则a是 数.
(4) 的相反数是 ,-3x的相反数是 .
5.已知数轴上A、B表示的数互为相反数,并且两点间的距离是6,点A在点B的左边,则点A、B表示的数分别是 .
1.6
-0.3
-a
13
6
正
正
3x
-3,3
课堂小结
肆
课堂小结
壹
相反数
定义
只有符号不同的两个数.
性质
a的相反数是-a,0的相反数是0.
互为相反数的两个数到原点的距离相等.
多重符号的化简
偶数个“-”号,结果为正数.
奇数个“-”号,结果为负数.
课后作业
基础题:1.课后习题 第 4题。
提高题:2.如图,在一条不完整的数轴上,动点A向左移动4个单位长度到达点B,再向右移动7个单位长度到达点C.如果点A、C表示的数互为相反数,求点B表示的数.
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
