1.2.4 绝对值 课件(共29张PPT)
文档属性
| 名称 | 1.2.4 绝对值 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 21:43:02 | ||
图片预览








文档简介
(共29张PPT)
1.2.4 绝对值
1.2 有理数
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
从一栋房子里,跑出两只狗(一灰一黄),有人在房子的西边3米处以及房子的东边3米处各放了一根骨头,两狗发现后,灰狗跑向西3米处,黄狗跑向东3米处分别衔起了骨头.
问题:1.在数轴上表示这一情景.
2.两只小狗它们所跑的路线相同吗?
3.两只小狗它们所跑的路程一样吗?
在实际生活中,有时存在这样的情况,有些问题我们只需要考虑数的大小而不考虑方向.在我们的数学中,就是不需要考虑数的正负性,比如:在计算小狗所跑的路程时,与狗跑的方向无关,这时所走的路程只需要用正数来表示,这样就必需引进一个新的概念——绝对值.
讲授新知
贰
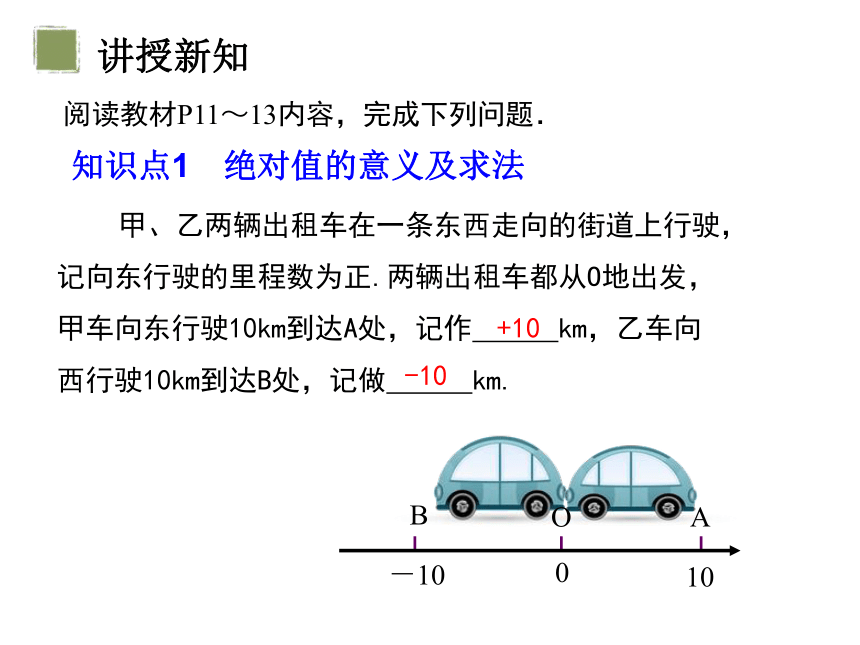
甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正.两辆出租车都从O地出发,甲车向东行驶10km到达A处,记作 km,乙车向西行驶10km到达B处,记做 km.
+10
-10
-10
10
0
O
B
A
讲授新知
阅读教材P11~13内容,完成下列问题.
知识点1 绝对值的意义及求法
2.以O为原点,取适当的单位长度画数轴,并在数轴上标出A、B的位置,则A、B两点与原点距离分别是多少?它们的实际意义是什么?
讲授新知
距离都是10km.它们的实际意义是A在O正东方向10km处,B在O正西方向10km处.
知识归纳:我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“| |”表示.
例1 (1)数轴上表示数2的点到原点的距离是 ,所以|2|= ;数轴上表示数-2的点到原点的距离是 ,所以|-2|= ;数轴上表示数0的点到原点的距离是 ,所以|0|= .
范例应用
2
2
2
0
(2)|4.5|= ,|-4.5|= ,即如果数轴上一点到原点的距离为4.5,那么这个点表示的数是 .
4.5
4.5
4.5或-4.5
2
0
讲授新课
观察与思考
知识点2 绝对值的性质及应用
观察这些数的绝对值,它们有什么共同点?
|5|=5,|-10|=10,|3.5|= 3.5,
|100|=100,|-3|=3,|50|=50,
|-4.5|=4.5,|-5000|=5000,|0|=0,…
思考1:(1)一个正数的绝对值是什么?(2)一个负数的绝对值是什么?
(3)0的绝对值是什么?
结论1:一个正数的绝对值是正数,一个负数的绝对值是正数,0的绝对值是0.
结论2:一个正数的绝对值是它本身.一个负数的绝对值是它的相反数.
即任何一个有理数的绝对值都是非负数
讲授新课
结论
思考2:若字母a表示一个有理数,你知道a的绝对值等于什么吗
讲授新课
(1)当a是正数时,|a|= ; 正数的绝对值是它本身.
(2)当a是负数时,|a|= ; 负数的绝对值是它的相反数.
(3)当a=0时,|a|= .0的绝对值是 .
a
-a
0
0
思考3:相反数、绝对值的联系是什么?
互为相反数的两个数的绝对值相等.绝对值相等,符号相反的两个数互为相反数.
范例应用
例2 求下列各数的绝对值:12, ,-7.5,0.
解:|12|=12,| |= ,|-7.5|=7.5,|0|=0.
例3 填空
(1)绝对值等于0的数是 ;
(2)绝对值等于5.25的正数是 ;
(3)绝对值等于5.25的负数是 ;
(4)绝对值等于2的数是 .
±2
5.25
0
-5.25
易错提醒:注意绝对值等于某个正数的数有两个,他们互为相反数,解题时不要遗漏负值.
讲授新课
知识点3 借助数轴比较有理数的大小
下图表示某一天我国5个城市的最低气温.
(1)将这5座城市这一天的最低气温按照由低到高的顺序排列出来.
哈尔滨(-20℃)<北京(-10℃)<上海(0℃)<武汉(5℃)<广州(10℃)
讲授新课
(2)将这5座城市这一天的最低气温在数轴上表示出来,这些数的大小与它们在数轴上所表示的点的位置有什么关系?
如图所示:
气温越高,对应的数越大,在数轴上所表示的点越靠右.
【自主归纳】
有理数大小的比较方法:
数轴比较法:在数轴上表示的两个数,右边的数总比左边的数大.
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
例3 在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
解:
-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-5 <-3 <0 <4
范例应用
讲授新课
知识点4 运用法则比较有理数的大小
问题:
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
结论:
(1)正数大于0,
负数小于0,
正数大于负数;
(2)两个负数,绝对值大的反而小.
例如,1 > 0,0 > -1,1 > -1,-1 > -2.
范例应用
例4 比较下列各数的大小.
(1)-(-3)和-(+2);
解:先化简,-(-3)=3,-(+2)=-2,
因为正数大于负数,
所以3>-2,即-(-3)>-(+2).
范例应用
例4 比较下列各数的大小.
(2) ;
解:两个负数做比较,先求它们的绝对值.
解:先化简:
范例应用
当堂训练
叁
1. 的绝对值是( )
A.-7 B.7 C. D.
2.在有理数2,-3, ,0中,最小的数是( )
A.2 B.-3 C. D.0
D
当堂训练
B
3. 的相反数是它本身, 的绝对值是它的相反数.
非负数
非正数
4. 的相反数是 ;若|a|=2,则a= .
±2
-
当堂训练
5.比较下列各对数的大小:
>
>
<
<
当堂训练
6.下表记录了今年一月某日部分城市的最高气温:
城市 阜阳 安庆 淮北 合肥 芜湖
最高气温/℃ -5 2 -3 -1 4
(1)在数轴上表示这些城市最高气温的值;
(2)用“<”连接这些城市的最高气温.
解:(1)如图
(2)-5℃<-3℃<-1℃<2℃<4℃
课堂小结
肆
课堂小结
壹
绝对值
定义
性质
几何定义
代数定义
|a|≥0
比较有理数大小
借助数轴比较有理数的大小
运用法则比较有理数的大小
课后作业
基础题:1.课后习题 第 5,6题。
提高题:2.课后习题 第 11,12题。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.2.4 绝对值
1.2 有理数
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
从一栋房子里,跑出两只狗(一灰一黄),有人在房子的西边3米处以及房子的东边3米处各放了一根骨头,两狗发现后,灰狗跑向西3米处,黄狗跑向东3米处分别衔起了骨头.
问题:1.在数轴上表示这一情景.
2.两只小狗它们所跑的路线相同吗?
3.两只小狗它们所跑的路程一样吗?
在实际生活中,有时存在这样的情况,有些问题我们只需要考虑数的大小而不考虑方向.在我们的数学中,就是不需要考虑数的正负性,比如:在计算小狗所跑的路程时,与狗跑的方向无关,这时所走的路程只需要用正数来表示,这样就必需引进一个新的概念——绝对值.
讲授新知
贰
甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正.两辆出租车都从O地出发,甲车向东行驶10km到达A处,记作 km,乙车向西行驶10km到达B处,记做 km.
+10
-10
-10
10
0
O
B
A
讲授新知
阅读教材P11~13内容,完成下列问题.
知识点1 绝对值的意义及求法
2.以O为原点,取适当的单位长度画数轴,并在数轴上标出A、B的位置,则A、B两点与原点距离分别是多少?它们的实际意义是什么?
讲授新知
距离都是10km.它们的实际意义是A在O正东方向10km处,B在O正西方向10km处.
知识归纳:我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“| |”表示.
例1 (1)数轴上表示数2的点到原点的距离是 ,所以|2|= ;数轴上表示数-2的点到原点的距离是 ,所以|-2|= ;数轴上表示数0的点到原点的距离是 ,所以|0|= .
范例应用
2
2
2
0
(2)|4.5|= ,|-4.5|= ,即如果数轴上一点到原点的距离为4.5,那么这个点表示的数是 .
4.5
4.5
4.5或-4.5
2
0
讲授新课
观察与思考
知识点2 绝对值的性质及应用
观察这些数的绝对值,它们有什么共同点?
|5|=5,|-10|=10,|3.5|= 3.5,
|100|=100,|-3|=3,|50|=50,
|-4.5|=4.5,|-5000|=5000,|0|=0,…
思考1:(1)一个正数的绝对值是什么?(2)一个负数的绝对值是什么?
(3)0的绝对值是什么?
结论1:一个正数的绝对值是正数,一个负数的绝对值是正数,0的绝对值是0.
结论2:一个正数的绝对值是它本身.一个负数的绝对值是它的相反数.
即任何一个有理数的绝对值都是非负数
讲授新课
结论
思考2:若字母a表示一个有理数,你知道a的绝对值等于什么吗
讲授新课
(1)当a是正数时,|a|= ; 正数的绝对值是它本身.
(2)当a是负数时,|a|= ; 负数的绝对值是它的相反数.
(3)当a=0时,|a|= .0的绝对值是 .
a
-a
0
0
思考3:相反数、绝对值的联系是什么?
互为相反数的两个数的绝对值相等.绝对值相等,符号相反的两个数互为相反数.
范例应用
例2 求下列各数的绝对值:12, ,-7.5,0.
解:|12|=12,| |= ,|-7.5|=7.5,|0|=0.
例3 填空
(1)绝对值等于0的数是 ;
(2)绝对值等于5.25的正数是 ;
(3)绝对值等于5.25的负数是 ;
(4)绝对值等于2的数是 .
±2
5.25
0
-5.25
易错提醒:注意绝对值等于某个正数的数有两个,他们互为相反数,解题时不要遗漏负值.
讲授新课
知识点3 借助数轴比较有理数的大小
下图表示某一天我国5个城市的最低气温.
(1)将这5座城市这一天的最低气温按照由低到高的顺序排列出来.
哈尔滨(-20℃)<北京(-10℃)<上海(0℃)<武汉(5℃)<广州(10℃)
讲授新课
(2)将这5座城市这一天的最低气温在数轴上表示出来,这些数的大小与它们在数轴上所表示的点的位置有什么关系?
如图所示:
气温越高,对应的数越大,在数轴上所表示的点越靠右.
【自主归纳】
有理数大小的比较方法:
数轴比较法:在数轴上表示的两个数,右边的数总比左边的数大.
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
例3 在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
解:
-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-5 <-3 <0 <4
范例应用
讲授新课
知识点4 运用法则比较有理数的大小
问题:
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
结论:
(1)正数大于0,
负数小于0,
正数大于负数;
(2)两个负数,绝对值大的反而小.
例如,1 > 0,0 > -1,1 > -1,-1 > -2.
范例应用
例4 比较下列各数的大小.
(1)-(-3)和-(+2);
解:先化简,-(-3)=3,-(+2)=-2,
因为正数大于负数,
所以3>-2,即-(-3)>-(+2).
范例应用
例4 比较下列各数的大小.
(2) ;
解:两个负数做比较,先求它们的绝对值.
解:先化简:
范例应用
当堂训练
叁
1. 的绝对值是( )
A.-7 B.7 C. D.
2.在有理数2,-3, ,0中,最小的数是( )
A.2 B.-3 C. D.0
D
当堂训练
B
3. 的相反数是它本身, 的绝对值是它的相反数.
非负数
非正数
4. 的相反数是 ;若|a|=2,则a= .
±2
-
当堂训练
5.比较下列各对数的大小:
>
>
<
<
当堂训练
6.下表记录了今年一月某日部分城市的最高气温:
城市 阜阳 安庆 淮北 合肥 芜湖
最高气温/℃ -5 2 -3 -1 4
(1)在数轴上表示这些城市最高气温的值;
(2)用“<”连接这些城市的最高气温.
解:(1)如图
(2)-5℃<-3℃<-1℃<2℃<4℃
课堂小结
肆
课堂小结
壹
绝对值
定义
性质
几何定义
代数定义
|a|≥0
比较有理数大小
借助数轴比较有理数的大小
运用法则比较有理数的大小
课后作业
基础题:1.课后习题 第 5,6题。
提高题:2.课后习题 第 11,12题。
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
