1.5.1 有理数的乘方 第1课时 有理数的乘方 课件(共26张PPT)
文档属性
| 名称 | 1.5.1 有理数的乘方 第1课时 有理数的乘方 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
1.5.1 乘 方
第1课时 有理数的乘方
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
古希腊数学家阿基米德与国王下棋,国王输了,问阿基米德要什么奖赏.阿基米德对国王说:“我只要在棋盘上第一格放一颗麦子,在第二个格子中放进前一个格子的两倍,每一个格子中都是前一个格子中麦子数量的两倍,一直将棋盘每一个格子摆满.”国王觉得很容易就可以满足他的要求,于是就同意了.但很快国王就发现,即使将国库所有的粮食都给他也不够.你们知道这是为什么吗?
讲授新知
贰
讲授新知
阅读教材P41~42内容,完成下列问题.
知识点1 乘方的意义
问题 某种细胞每30分钟便由一个分裂成两个.经过3小时这种细胞由1个能分裂成多少个?
合作探究
讲授新知
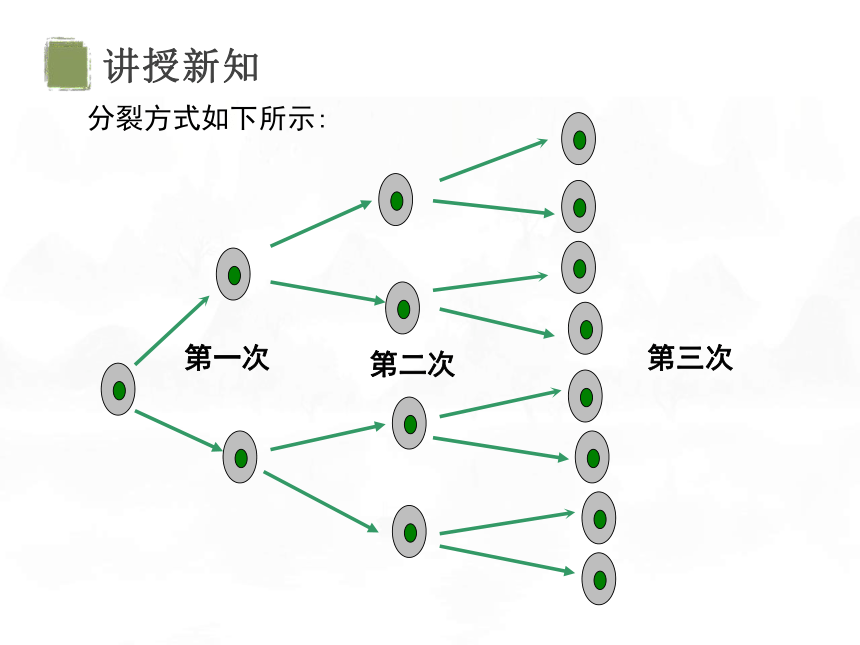
第一次
第二次
第三次
分裂方式如下所示:
讲授新知
这个细胞分裂一次可得多少个细胞
那么3小时共分裂了多少次 有多少个细胞?
解:一次得:
两次:
三次:
四次:
2个;
2×2个;
2×2×2个;
六次: 2×2×2×2×2×2个.
分裂两次呢
分裂三次呢 四次呢?
思考:
2×2×2×2个
讲授新知
问题 这两个式子有什么相同点
它们都是乘法;并且它们各自的因数都相同.
思考 同学们想一想:这样的运算能像平方、立方那样简写吗?
请比较细胞分裂四次后的个数式子:2×2×2×2
和细胞分裂六次后的个数式子: 2×2×2×2×2×2.
讲授新知
例如:2×2×2×2
2×2×2×2×2×2
记作
记作
知识要点
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
a·a·a· ·a = an
n个
…
读作2的6次方(幂).
读作2的4次方(幂).
讲授新知
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
幂
指数
因数的个数
底数
因数
知识要点
一个数可以看作这个数本身的一次方,例如8就是81,指数1通常省略不写.
讲授新知
(1)(-3)2的底数是_____,指数是_____,(-3)2表示2个_____相乘,读作_____的2次方,也读作-3的_____.
(2) 表示 __ 个 相乘,读作 的 __ 次方,也读作 的 次幂,其中 叫做 ,5叫做 .
温馨提示:幂的底数是分数或负数时,底数应该添上括号!
填一填
-3
2
-3
-3
平方
5
5
5
底数
指数
范例应用
例1 计算:(1)-(-3)3; (2)(- )2;
(3)(- )3; (4)(-1)2023.
解:(1)原式=-(-33)=33=3×3×3=27;
(2)原式=
(3)原式=-
(3)原式= -1.
【方法归纳】乘方的运算可以利用乘法的运算来进行.负数的奇数次幂是负数,负数的偶数次幂是正数;-1的奇数次幂是-1,-1的偶数次幂是1.
范例应用
例2 用计算器计算(-8)5和(-3)6.
解:用带符号键 的计算器.
(-)
=
)
(-)
(
<
8
5
显示:(-8) 5
<
-32768.
=
)
(-)
(
<
3
6
显示:(-3) 6
<
729.
所以(-8)5=-32768,(-3)6=729.
范例应用
(-2)2与-22
观察下面两个式子有什么不同?
(-2)2表示-2的平方,-22表示2的平方的相反数.
议一议
(-2)2与-22 互为相反数
讲授新课
知识点2 乘方的运算
例3 计算
(1)
(2)-23×(-32)
(3)64÷(-2)5
(4)(-4)3÷(-1)200+2×(-3)4
讲授新课
(2)-23×(-32)=-8×(-9)=72;
(3)64÷(-2)5=64÷(-32)=-2;
(4)(-4)3÷(-1)200+2×(-3)4=-64÷1+2×81=98
思考:通过以上计算,对于乘除和乘方的混合运算,你觉得有怎样的运算顺序?
先算乘方,后算乘除;如果遇到括号就先进行括号里的运算.
当堂训练
叁
当堂训练
1.算式(- )×(- )×(- )×(- )可表示为( )
A.(- )4 B.(- )×4
C.-( )4 D.以上答案均不对
2.关于-74的说法正确的是( )
A.底数是-7 B.表示4个-7相乘
C.表示4个7相乘的积的相反数 D.表示7个-4相乘
3.现规定一种新的运算“○”:m○n=mn,如3○2=32=9,则(- )○3的值为( )
A. B.- C.- D.-
B
A
C
当堂训练
4.计算:
(1)-42×(-4)2;
解:原式=-256.
解:原式= .
5.你吃过拉面吗?拉面是把1根面条对折成2根拉开,再对折成4根……依次这样进行对折,对折10次有多少根面条?有128根面条时对折了多少次?
解:210=1024(根),128=27.答:对折10次有1024根面条,有128根面条时对折了7次.
课堂小结
肆
课堂小结
壹
乘方
意义
求几个相同因数的积的运算,叫做乘方
符号法则
正数的任何次幂都是正数
负数的奇次幂是负数,
负数的偶次幂是正数
零的正整数次幂都是零
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2. 13世纪数学家斐波那契的《计算书》中有这样一个问题:“在罗马有7位老妇人,每人赶着7头毛驴,每头驴驮着7只口袋,每只口袋里装着7个面包,每个面包附有7把餐刀,每把餐刀有7只刀鞘”,求总刀鞘数.
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.5.1 乘 方
第1课时 有理数的乘方
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
古希腊数学家阿基米德与国王下棋,国王输了,问阿基米德要什么奖赏.阿基米德对国王说:“我只要在棋盘上第一格放一颗麦子,在第二个格子中放进前一个格子的两倍,每一个格子中都是前一个格子中麦子数量的两倍,一直将棋盘每一个格子摆满.”国王觉得很容易就可以满足他的要求,于是就同意了.但很快国王就发现,即使将国库所有的粮食都给他也不够.你们知道这是为什么吗?
讲授新知
贰
讲授新知
阅读教材P41~42内容,完成下列问题.
知识点1 乘方的意义
问题 某种细胞每30分钟便由一个分裂成两个.经过3小时这种细胞由1个能分裂成多少个?
合作探究
讲授新知
第一次
第二次
第三次
分裂方式如下所示:
讲授新知
这个细胞分裂一次可得多少个细胞
那么3小时共分裂了多少次 有多少个细胞?
解:一次得:
两次:
三次:
四次:
2个;
2×2个;
2×2×2个;
六次: 2×2×2×2×2×2个.
分裂两次呢
分裂三次呢 四次呢?
思考:
2×2×2×2个
讲授新知
问题 这两个式子有什么相同点
它们都是乘法;并且它们各自的因数都相同.
思考 同学们想一想:这样的运算能像平方、立方那样简写吗?
请比较细胞分裂四次后的个数式子:2×2×2×2
和细胞分裂六次后的个数式子: 2×2×2×2×2×2.
讲授新知
例如:2×2×2×2
2×2×2×2×2×2
记作
记作
知识要点
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
a·a·a· ·a = an
n个
…
读作2的6次方(幂).
读作2的4次方(幂).
讲授新知
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
幂
指数
因数的个数
底数
因数
知识要点
一个数可以看作这个数本身的一次方,例如8就是81,指数1通常省略不写.
讲授新知
(1)(-3)2的底数是_____,指数是_____,(-3)2表示2个_____相乘,读作_____的2次方,也读作-3的_____.
(2) 表示 __ 个 相乘,读作 的 __ 次方,也读作 的 次幂,其中 叫做 ,5叫做 .
温馨提示:幂的底数是分数或负数时,底数应该添上括号!
填一填
-3
2
-3
-3
平方
5
5
5
底数
指数
范例应用
例1 计算:(1)-(-3)3; (2)(- )2;
(3)(- )3; (4)(-1)2023.
解:(1)原式=-(-33)=33=3×3×3=27;
(2)原式=
(3)原式=-
(3)原式= -1.
【方法归纳】乘方的运算可以利用乘法的运算来进行.负数的奇数次幂是负数,负数的偶数次幂是正数;-1的奇数次幂是-1,-1的偶数次幂是1.
范例应用
例2 用计算器计算(-8)5和(-3)6.
解:用带符号键 的计算器.
(-)
=
)
(-)
(
<
8
5
显示:(-8) 5
<
-32768.
=
)
(-)
(
<
3
6
显示:(-3) 6
<
729.
所以(-8)5=-32768,(-3)6=729.
范例应用
(-2)2与-22
观察下面两个式子有什么不同?
(-2)2表示-2的平方,-22表示2的平方的相反数.
议一议
(-2)2与-22 互为相反数
讲授新课
知识点2 乘方的运算
例3 计算
(1)
(2)-23×(-32)
(3)64÷(-2)5
(4)(-4)3÷(-1)200+2×(-3)4
讲授新课
(2)-23×(-32)=-8×(-9)=72;
(3)64÷(-2)5=64÷(-32)=-2;
(4)(-4)3÷(-1)200+2×(-3)4=-64÷1+2×81=98
思考:通过以上计算,对于乘除和乘方的混合运算,你觉得有怎样的运算顺序?
先算乘方,后算乘除;如果遇到括号就先进行括号里的运算.
当堂训练
叁
当堂训练
1.算式(- )×(- )×(- )×(- )可表示为( )
A.(- )4 B.(- )×4
C.-( )4 D.以上答案均不对
2.关于-74的说法正确的是( )
A.底数是-7 B.表示4个-7相乘
C.表示4个7相乘的积的相反数 D.表示7个-4相乘
3.现规定一种新的运算“○”:m○n=mn,如3○2=32=9,则(- )○3的值为( )
A. B.- C.- D.-
B
A
C
当堂训练
4.计算:
(1)-42×(-4)2;
解:原式=-256.
解:原式= .
5.你吃过拉面吗?拉面是把1根面条对折成2根拉开,再对折成4根……依次这样进行对折,对折10次有多少根面条?有128根面条时对折了多少次?
解:210=1024(根),128=27.答:对折10次有1024根面条,有128根面条时对折了7次.
课堂小结
肆
课堂小结
壹
乘方
意义
求几个相同因数的积的运算,叫做乘方
符号法则
正数的任何次幂都是正数
负数的奇次幂是负数,
负数的偶次幂是正数
零的正整数次幂都是零
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2. 13世纪数学家斐波那契的《计算书》中有这样一个问题:“在罗马有7位老妇人,每人赶着7头毛驴,每头驴驮着7只口袋,每只口袋里装着7个面包,每个面包附有7把餐刀,每把餐刀有7只刀鞘”,求总刀鞘数.
谢
谢
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
