2.2 二次函数的图象与性质(第2课时) 课件(18张PPT)
文档属性
| 名称 | 2.2 二次函数的图象与性质(第2课时) 课件(18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 11:27:32 | ||
图片预览





文档简介
(共18张PPT)
2.2 二次函数的图象与性质
(第二课时)
北师大版 九年级下册
知识点回顾
一般地,抛物线y=ax2 的对称轴是_________,顶点是_________;
1)当 a>0时 ,抛物线的开口向______,顶点是抛物线的最_________点,
当x<0时,y随x的增大而_________;
当x>0时,y随x的增大而_________;
当x=0时,y有最_____值为_____。
2)当 a<0时 ,抛物线的开口向_____ __,顶点是抛物线的最________点,
当x<0时,y随x的增大而_________;
当x>0时,y随x的增大而_________;
当x=0时,y有最_____值为_____。
|a|越大,抛物线的开口_________。
y=ax2与y= -ax2关于________轴对称。
y轴
(0,0)
上
下
高
低
增大
增大
减小
减小
大
小
0
0
小
x
课前导入
学习目标
1)利用描点法画出二次函数y=ax2+k图象。
2)掌握抛物线y=ax2+k与抛物线y=ax2的相互关系。
3)理解并掌握抛物线y=ax2+k的性质。
重点
掌握抛物线y=ax2+k与抛物线y=ax2的相互关系。
难点
理解并掌握抛物线y=ax2+k的性质。
探索与思考
… -2 -1 0 1 2 …
…
…
9
3
1
3
9
…
…
7
1
-1
1
7
根据表中x,y的数值在坐标平面中描出对应的点。
3
6
9
y
O
-3
3
x
通过描点法画出?
用平滑曲线顺次连接各点,就得到图象。
+1
-1
探索与思考
3
6
9
y
O
-3
3
x
+1
-1
开口方向 对称轴 顶点坐标
向上
y轴
(0,1)
向上
y轴
(0,-1)
抛物线的开口方向、对称轴和顶点各是什么?
探索与思考
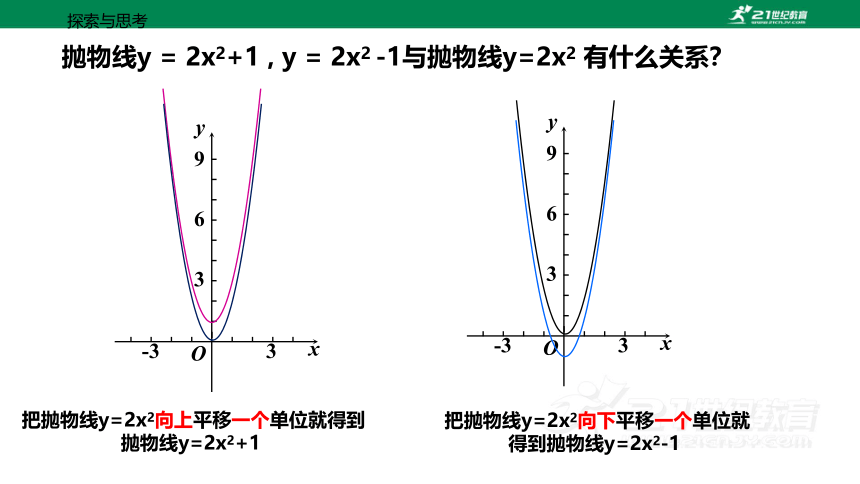
抛物线y = 2x2+1 , y = 2x2 -1与抛物线y=2x2 有什么关系?
3
6
9
y
O
-3
3
x
3
6
9
y
O
-3
3
x
把抛物线y=2x2向上平移一个单位就得到抛物线y=2x2+1
把抛物线y=2x2向下平移一个单位就得到抛物线y=2x2-1
探索与思考
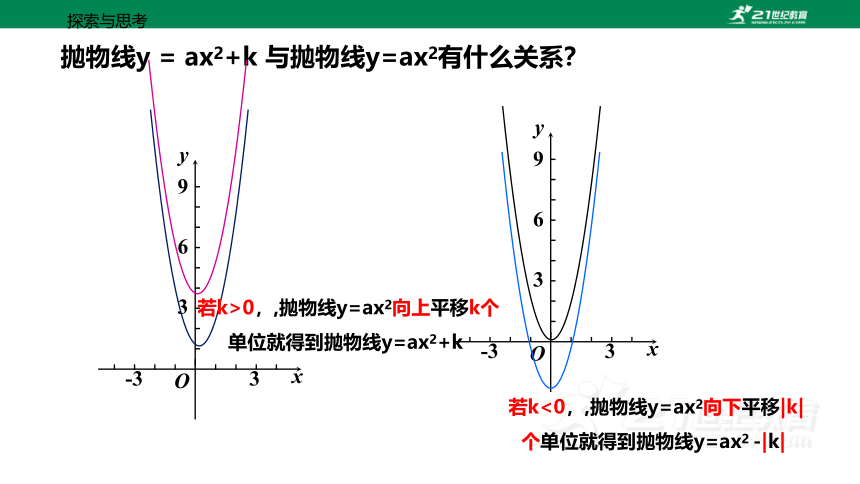
抛物线y = ax2+k 与抛物线y=ax2有什么关系?
3
6
9
y
O
-3
3
x
3
6
9
y
O
-3
3
x
若k>0,,抛物线y=ax2向上平移k个单位就得到抛物线y=ax2+k
若k<0,,抛物线y=ax2向下平移|k|个单位就得到抛物线y=ax2 -|k|
探索与思考
抛物线y = ax2+k 与抛物线y=ax2 有什么关系?
抛物线y=ax2+k的图象相当于把抛物线y=ax2的图象 (k>0)或 (k<0)平移 个单位.
向上
向下
|k|
小组讨论
通过描点法画出?
【思考】抛物线,与抛物线y= x2 有何关系?
课堂小结
抛物线y = ax2+k a>0 a<0
图象 k>0
k<0
开口方向
对称轴 顶点坐标 函数的增减性
最值
x=0时,y最小值=k
x=0时,y最大值=k
当x<0时,y随x增大而增大;
当x>0时,y随x增大而减小.
当x<0时,y随x增大而减小;
当x>0时,y随x增大而增大.
向上
向下
y轴(直线x=0)
(0,k)
课堂基础练
1.抛物线的对称轴是直线( )
A.x=2 B.x=0 C.y=0 D.y=2
【详解】解:由抛物线可知:对称轴为直线;故选B.
2.抛物线的顶点坐标为( )
A. B. C. D.
【详解】解:的对称轴为x=0,开口向上,y的最小值为4,顶点坐标为(0,4),故选: B.
课堂基础练
3.二次函数y=﹣x2﹣4的图象经过的象限为( )
A.第一象限、第四象限 B.第二象限、第四象限
C.第三象限、第四象限 D.第一象限、第三象限、第四象限
【详解】解:∵y=﹣x2﹣4,∴抛物线对称轴为y轴,顶点坐标为(0,﹣4),开口向下,∴抛物线经过第三,四象限,故选:C.
4.函数与的图象的不同之处是( )
A.顶点 B.对称轴 C.开口方向 D.形状
【详解】解:函数与由,所以抛物线的开口方向,形状相同,
又对称轴都为轴,所以对称轴相同,
的顶点为:
的顶点为:(0,-2) 所以两条抛物线的顶点不同,故A符合题意.
课堂基础练
5.二次函数y=x2+1的图象大致是( )
【详解】解:二次函数y=x2+1中,
a=1>0,图象开口向上,顶点坐标为(0,1),
符合条件的图象是B.故选B.
6.在直角坐标系中,函数y= 3x与y= -x2+1的图像大致是( )
【详解】由一次函数的性质可知,y= 3x的函数图像过一、三象限,由二次函数性质可得y= -x2+1中a<0,抛物线开口向下,故选D.
随堂测试
7.二次函数在内的最小值是( )
A.3 B.2 C.-29 D.-30
【详解】解:由图可知,当x=4时,函数取得最小值y最小值=-2×16+3=-29.故选:C.
8.二次函数y=3x2-3的图象开口向_____,顶点坐标为_____,对称轴为_____,当x>0时,y随x的增大而_____;当x<0时,y随x的增大而_____.因为a=3>0,所以y有最_____值,当x=_____时,y的最_____值是_____.
【详解】
二次函数y=3x2-3中k=3,所以开口向上,顶点坐标(0,-3),对称轴为y轴,当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小.因为a=3>0,所以y有最小值,当x=0时,y的最小值是-3.
随堂测试
9.已知函数是关于x的二次函数.
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
【详解】1)∵函数是关于x的二次函数,∴m2+m﹣4=2,
解得:m1=2,m2=﹣3;
2)当m=2时,抛物线有最低点,此时y=4x2+1,则最低点为:(0,1),
由于抛物线的对称轴为y轴,故当x>0时,y随x的增大而增大;
随堂测试
9.已知函数是关于x的二次函数.
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
(3)当m=﹣3时,函数有最大值,
此时y=﹣x2+1,故此函数有最大值1,
由于抛物线的对称轴为y轴,
故当x>0时,y随x的增大而减小.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.2 二次函数的图象与性质
(第二课时)
北师大版 九年级下册
知识点回顾
一般地,抛物线y=ax2 的对称轴是_________,顶点是_________;
1)当 a>0时 ,抛物线的开口向______,顶点是抛物线的最_________点,
当x<0时,y随x的增大而_________;
当x>0时,y随x的增大而_________;
当x=0时,y有最_____值为_____。
2)当 a<0时 ,抛物线的开口向_____ __,顶点是抛物线的最________点,
当x<0时,y随x的增大而_________;
当x>0时,y随x的增大而_________;
当x=0时,y有最_____值为_____。
|a|越大,抛物线的开口_________。
y=ax2与y= -ax2关于________轴对称。
y轴
(0,0)
上
下
高
低
增大
增大
减小
减小
大
小
0
0
小
x
课前导入
学习目标
1)利用描点法画出二次函数y=ax2+k图象。
2)掌握抛物线y=ax2+k与抛物线y=ax2的相互关系。
3)理解并掌握抛物线y=ax2+k的性质。
重点
掌握抛物线y=ax2+k与抛物线y=ax2的相互关系。
难点
理解并掌握抛物线y=ax2+k的性质。
探索与思考
… -2 -1 0 1 2 …
…
…
9
3
1
3
9
…
…
7
1
-1
1
7
根据表中x,y的数值在坐标平面中描出对应的点。
3
6
9
y
O
-3
3
x
通过描点法画出?
用平滑曲线顺次连接各点,就得到图象。
+1
-1
探索与思考
3
6
9
y
O
-3
3
x
+1
-1
开口方向 对称轴 顶点坐标
向上
y轴
(0,1)
向上
y轴
(0,-1)
抛物线的开口方向、对称轴和顶点各是什么?
探索与思考
抛物线y = 2x2+1 , y = 2x2 -1与抛物线y=2x2 有什么关系?
3
6
9
y
O
-3
3
x
3
6
9
y
O
-3
3
x
把抛物线y=2x2向上平移一个单位就得到抛物线y=2x2+1
把抛物线y=2x2向下平移一个单位就得到抛物线y=2x2-1
探索与思考
抛物线y = ax2+k 与抛物线y=ax2有什么关系?
3
6
9
y
O
-3
3
x
3
6
9
y
O
-3
3
x
若k>0,,抛物线y=ax2向上平移k个单位就得到抛物线y=ax2+k
若k<0,,抛物线y=ax2向下平移|k|个单位就得到抛物线y=ax2 -|k|
探索与思考
抛物线y = ax2+k 与抛物线y=ax2 有什么关系?
抛物线y=ax2+k的图象相当于把抛物线y=ax2的图象 (k>0)或 (k<0)平移 个单位.
向上
向下
|k|
小组讨论
通过描点法画出?
【思考】抛物线,与抛物线y= x2 有何关系?
课堂小结
抛物线y = ax2+k a>0 a<0
图象 k>0
k<0
开口方向
对称轴 顶点坐标 函数的增减性
最值
x=0时,y最小值=k
x=0时,y最大值=k
当x<0时,y随x增大而增大;
当x>0时,y随x增大而减小.
当x<0时,y随x增大而减小;
当x>0时,y随x增大而增大.
向上
向下
y轴(直线x=0)
(0,k)
课堂基础练
1.抛物线的对称轴是直线( )
A.x=2 B.x=0 C.y=0 D.y=2
【详解】解:由抛物线可知:对称轴为直线;故选B.
2.抛物线的顶点坐标为( )
A. B. C. D.
【详解】解:的对称轴为x=0,开口向上,y的最小值为4,顶点坐标为(0,4),故选: B.
课堂基础练
3.二次函数y=﹣x2﹣4的图象经过的象限为( )
A.第一象限、第四象限 B.第二象限、第四象限
C.第三象限、第四象限 D.第一象限、第三象限、第四象限
【详解】解:∵y=﹣x2﹣4,∴抛物线对称轴为y轴,顶点坐标为(0,﹣4),开口向下,∴抛物线经过第三,四象限,故选:C.
4.函数与的图象的不同之处是( )
A.顶点 B.对称轴 C.开口方向 D.形状
【详解】解:函数与由,所以抛物线的开口方向,形状相同,
又对称轴都为轴,所以对称轴相同,
的顶点为:
的顶点为:(0,-2) 所以两条抛物线的顶点不同,故A符合题意.
课堂基础练
5.二次函数y=x2+1的图象大致是( )
【详解】解:二次函数y=x2+1中,
a=1>0,图象开口向上,顶点坐标为(0,1),
符合条件的图象是B.故选B.
6.在直角坐标系中,函数y= 3x与y= -x2+1的图像大致是( )
【详解】由一次函数的性质可知,y= 3x的函数图像过一、三象限,由二次函数性质可得y= -x2+1中a<0,抛物线开口向下,故选D.
随堂测试
7.二次函数在内的最小值是( )
A.3 B.2 C.-29 D.-30
【详解】解:由图可知,当x=4时,函数取得最小值y最小值=-2×16+3=-29.故选:C.
8.二次函数y=3x2-3的图象开口向_____,顶点坐标为_____,对称轴为_____,当x>0时,y随x的增大而_____;当x<0时,y随x的增大而_____.因为a=3>0,所以y有最_____值,当x=_____时,y的最_____值是_____.
【详解】
二次函数y=3x2-3中k=3,所以开口向上,顶点坐标(0,-3),对称轴为y轴,当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小.因为a=3>0,所以y有最小值,当x=0时,y的最小值是-3.
随堂测试
9.已知函数是关于x的二次函数.
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
【详解】1)∵函数是关于x的二次函数,∴m2+m﹣4=2,
解得:m1=2,m2=﹣3;
2)当m=2时,抛物线有最低点,此时y=4x2+1,则最低点为:(0,1),
由于抛物线的对称轴为y轴,故当x>0时,y随x的增大而增大;
随堂测试
9.已知函数是关于x的二次函数.
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
(3)当m=﹣3时,函数有最大值,
此时y=﹣x2+1,故此函数有最大值1,
由于抛物线的对称轴为y轴,
故当x>0时,y随x的增大而减小.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
