2.2 二次函数的图象与性质(第1课时) 课件(18张PPT)
文档属性
| 名称 | 2.2 二次函数的图象与性质(第1课时) 课件(18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 09:31:41 | ||
图片预览





文档简介
(共18张PPT)
2.2 二次函数的图象与性质
(第一课时)
北师大版 九年级下册
课前回顾
简述描点法作图的一般步骤?
1)列表—表中给出一些自变量的值及其对应的函数值;
2)描点—在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
3)连线—按照横坐标由小到大顺序,把所描出的各点用平滑的曲线连接起来。
你能通过这种方法画出二次函数的图象吗?
课前导入
学习目标
1)利用描点法画出y=a图象。
2)通过图象了解二次函数图象的性质。
重点
利用描点法画出y=a图象。
难点
能够熟练画出二次函数的图象,理解并掌握二次函数的性质。
探索与思考
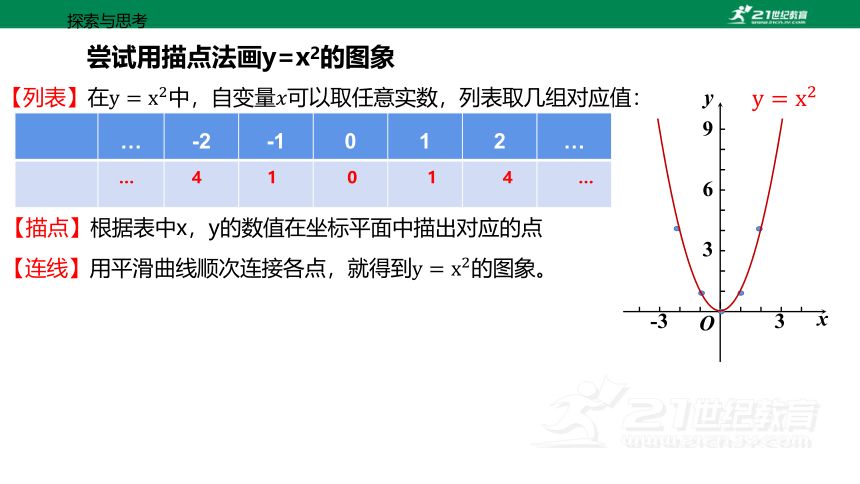
尝试用描点法画y=x2的图象
… -2 -1 0 1 2 …
…
…
4
1
0
1
4
【列表】在列表取几组对应值:
【描点】根据表中x,y的数值在坐标平面中描出对应的点
【连线】用平滑曲线顺次连接各点,就得到的图象。
3
6
9
y
O
-3
3
x
探索与思考
特征:开口向上的曲线
形状:类似于u形磁铁。
事实上,二次函数的图象都是抛物线,它们的开口或者向上或者下。一般地,二次函数 y =ax2+bx +c(a≠0)的图象叫做抛物线y=ax2+bx+c.
3
6
9
y
O
-3
3
x
观察y=x2的图象,它有什么特征?它的形状像什么?
探索与思考
3
6
9
y
O
-3
3
x
交点坐标(0,0),
观察图象,当二次函数的x=0时,y=0(最小值)
这条抛物线关于y轴对称,y轴就是它的对称轴.
实际上,每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线的顶点。
【切记】顶点是抛物线的最低点或最高点。
P(-1,1)
P’(1,1)
观察y=x2的图象,它的对称轴在哪里?图象与y轴交点坐标?
探索与思考
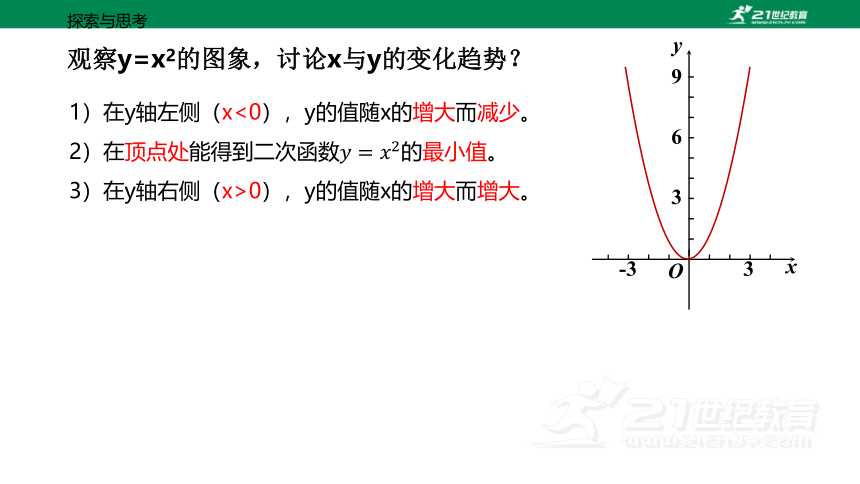
观察y=x2的图象,讨论x与y的变化趋势?
3
6
9
y
O
-3
3
x
1)在y轴左侧(x<0),y的值随x的增大而减少。
2)在顶点处能得到二次函数的最小值。
3)在y轴右侧(x>0),y的值随x的增大而增大。
探索与思考
y=x2
y=2x2
1)开口都向上(a>0) ,对称轴都是y轴。
2)当x<0时,y随x增大而减小;
当x>0时,y随x增大而增大。
3)顶点是原点(最小值)。
4)a值越大抛物线开口越小。
y=x2
对比函数y = x2, y=x2 ,y = 2x2的图象,你发现了什么?
探索与思考
对比函数y =- x2, y=-x2 ,y = -2x2的图象,你发现了什么?
y=-x2
y=-2x2
y=-x2
1)开口都向下(a<0),对称轴都是y轴。
2)当x<0时,y随x增大而增大;
当x>0时,y随x增大而减小。
3)顶点是原点(最大值)。
4)a值越小抛物线开口越小。
课堂小结
一般地,抛物线y=ax2 的对称轴是_________,顶点是_________;
1)当 a>0时 ,抛物线的开口向______,顶点是抛物线的最_________点,
当x<0时,y随x的增大而_________;
当x>0时,y随x的增大而_________;
当x=0时,y有最_____值为_____。
2)当 a<0时 ,抛物线的开口向_____ __,顶点是抛物线的最________点,
当x<0时,y随x的增大而_________;
当x>0时,y随x的增大而_________;
当x=0时,y有最_____值为_____。
|a|越大,抛物线的开口_________。
y=ax2与y= -ax2关于________轴对称。
y轴
(0,0)
上
下
高
低
增大
增大
减小
减小
大
小
0
0
小
x
课堂基础练
1 函数y=ax2(a≠0)的图象与a的符号有关的是( )
A.对称轴 B.顶点坐标 C.开口方向 D.开口大小
2. 已知点(-2,),(0,),(1,)都在函数的图象上,则( )
A.>> B.>>
C.>> D.>>
【详解】解:二次函数图象中a的符号决定了抛物线的开口方向,故选C.
【详解】函数的图象的对称轴是y轴,顶点是原点,开口向上,所以离原点越远,函数值就越大.因为|-2|>1>0,所以y1>y3>y2.故选B.
课堂基础练
3.下列四个二次函数:①y=x2,②y=﹣2x2,③,④y=3x2,其中抛物线开口从大到小的排列顺序是( )
A.③①②④ B.②③①④ C.④②①③ D.④①③②
4 .函数y=ax2(a≠0)的图象经过点(a,8),则a的值为()
A.±2 B.-2 C.2 D.3
【详解】解:∵<1<|﹣2|<3,∴抛物线开口从大到小的排列顺序是③①②④,故选A.
【详解】把点(a,8)代入:y=ax2得:a3=8,解得:a=2.故选C.
随堂测试
5.下列关于二次函数y=2x2的说法正确的是( )
A.它的图象经过点(,) B.它的图象的对称轴是直线x=2
C.当x<0时,y随x的增大而减小 D.当x=0时,y有最大值为0
【详解】
解:A、当x=0时,y=0≠2,故此选项错误;
B、它的图象的对称轴是直线x=0,故此选项错误;
C、当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大,故此选项正确;
D、当x=0时,y有最小值是0,故此选项错误;
故选:C.
随堂测试
6.下列说法中错误的是( )
A.在函数y=﹣x2 中,当x=0时y有最大值0
B.在函数y= 2x2中,当x>0时y随x的增大而增大
C.抛物线y=2x2,y=﹣x2,y=﹣中,抛物线y=2x2的开口最小,抛物线y=﹣x2的开口最大
D.不论a是正数还是负数,抛物线y=ax2的顶点都是坐标原点
【详解】
由函数的解析式y=-x2,可知a=-1<0,得到函数的开口向下,有最大值y=0,故A正确;
由函数的解析式y=2x2,可知其对称轴为y轴,对称轴的左边(x<0),y随x增大而减小,对称轴的右边(x>0),y随x增大而增大,故B正确;
根据二次函数的性质,可知系数a决定开口方向和开口大小,且a的绝对值越大,函数图象开口越小,可知抛物线y=2x2的开口最小,抛物线y=-x2的开口第二小,而开口最大,故不正确;不论a是正数还是负数,抛物线y=ax2的顶点都是坐标原点,正确.
故选C.
随堂测试
7 如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=x2与y=–x2的图象,则阴影部分的面积是__________.
【详解】
函数y=x2与y=–x2的图象关于x轴对称,又因正方形的边长为4,以正方形中心为原点建立平面直角坐标系,所以阴影部分的面积为正方形面积的一半,即4×4×=8.
随堂测试
8 在同一直角坐标系中,函数y=ax2(a≠0)与y=ax(a≠0)的大致图象可能是( )
【详解】
∵y=ax(a≠0)的图象是一条经过原点的直线,所以A不正确;
∵当a>0时,y=ax (a≠0)的开口向上,y=ax(a≠0的的图象经过第一,第三象限,当a<0时y=ax (a≠0)的开口向下,y=ax(a≠0)的图象经过第二,第四象限,∴选项B,D不正确,
选项C正确。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.2 二次函数的图象与性质
(第一课时)
北师大版 九年级下册
课前回顾
简述描点法作图的一般步骤?
1)列表—表中给出一些自变量的值及其对应的函数值;
2)描点—在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
3)连线—按照横坐标由小到大顺序,把所描出的各点用平滑的曲线连接起来。
你能通过这种方法画出二次函数的图象吗?
课前导入
学习目标
1)利用描点法画出y=a图象。
2)通过图象了解二次函数图象的性质。
重点
利用描点法画出y=a图象。
难点
能够熟练画出二次函数的图象,理解并掌握二次函数的性质。
探索与思考
尝试用描点法画y=x2的图象
… -2 -1 0 1 2 …
…
…
4
1
0
1
4
【列表】在列表取几组对应值:
【描点】根据表中x,y的数值在坐标平面中描出对应的点
【连线】用平滑曲线顺次连接各点,就得到的图象。
3
6
9
y
O
-3
3
x
探索与思考
特征:开口向上的曲线
形状:类似于u形磁铁。
事实上,二次函数的图象都是抛物线,它们的开口或者向上或者下。一般地,二次函数 y =ax2+bx +c(a≠0)的图象叫做抛物线y=ax2+bx+c.
3
6
9
y
O
-3
3
x
观察y=x2的图象,它有什么特征?它的形状像什么?
探索与思考
3
6
9
y
O
-3
3
x
交点坐标(0,0),
观察图象,当二次函数的x=0时,y=0(最小值)
这条抛物线关于y轴对称,y轴就是它的对称轴.
实际上,每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线的顶点。
【切记】顶点是抛物线的最低点或最高点。
P(-1,1)
P’(1,1)
观察y=x2的图象,它的对称轴在哪里?图象与y轴交点坐标?
探索与思考
观察y=x2的图象,讨论x与y的变化趋势?
3
6
9
y
O
-3
3
x
1)在y轴左侧(x<0),y的值随x的增大而减少。
2)在顶点处能得到二次函数的最小值。
3)在y轴右侧(x>0),y的值随x的增大而增大。
探索与思考
y=x2
y=2x2
1)开口都向上(a>0) ,对称轴都是y轴。
2)当x<0时,y随x增大而减小;
当x>0时,y随x增大而增大。
3)顶点是原点(最小值)。
4)a值越大抛物线开口越小。
y=x2
对比函数y = x2, y=x2 ,y = 2x2的图象,你发现了什么?
探索与思考
对比函数y =- x2, y=-x2 ,y = -2x2的图象,你发现了什么?
y=-x2
y=-2x2
y=-x2
1)开口都向下(a<0),对称轴都是y轴。
2)当x<0时,y随x增大而增大;
当x>0时,y随x增大而减小。
3)顶点是原点(最大值)。
4)a值越小抛物线开口越小。
课堂小结
一般地,抛物线y=ax2 的对称轴是_________,顶点是_________;
1)当 a>0时 ,抛物线的开口向______,顶点是抛物线的最_________点,
当x<0时,y随x的增大而_________;
当x>0时,y随x的增大而_________;
当x=0时,y有最_____值为_____。
2)当 a<0时 ,抛物线的开口向_____ __,顶点是抛物线的最________点,
当x<0时,y随x的增大而_________;
当x>0时,y随x的增大而_________;
当x=0时,y有最_____值为_____。
|a|越大,抛物线的开口_________。
y=ax2与y= -ax2关于________轴对称。
y轴
(0,0)
上
下
高
低
增大
增大
减小
减小
大
小
0
0
小
x
课堂基础练
1 函数y=ax2(a≠0)的图象与a的符号有关的是( )
A.对称轴 B.顶点坐标 C.开口方向 D.开口大小
2. 已知点(-2,),(0,),(1,)都在函数的图象上,则( )
A.>> B.>>
C.>> D.>>
【详解】解:二次函数图象中a的符号决定了抛物线的开口方向,故选C.
【详解】函数的图象的对称轴是y轴,顶点是原点,开口向上,所以离原点越远,函数值就越大.因为|-2|>1>0,所以y1>y3>y2.故选B.
课堂基础练
3.下列四个二次函数:①y=x2,②y=﹣2x2,③,④y=3x2,其中抛物线开口从大到小的排列顺序是( )
A.③①②④ B.②③①④ C.④②①③ D.④①③②
4 .函数y=ax2(a≠0)的图象经过点(a,8),则a的值为()
A.±2 B.-2 C.2 D.3
【详解】解:∵<1<|﹣2|<3,∴抛物线开口从大到小的排列顺序是③①②④,故选A.
【详解】把点(a,8)代入:y=ax2得:a3=8,解得:a=2.故选C.
随堂测试
5.下列关于二次函数y=2x2的说法正确的是( )
A.它的图象经过点(,) B.它的图象的对称轴是直线x=2
C.当x<0时,y随x的增大而减小 D.当x=0时,y有最大值为0
【详解】
解:A、当x=0时,y=0≠2,故此选项错误;
B、它的图象的对称轴是直线x=0,故此选项错误;
C、当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大,故此选项正确;
D、当x=0时,y有最小值是0,故此选项错误;
故选:C.
随堂测试
6.下列说法中错误的是( )
A.在函数y=﹣x2 中,当x=0时y有最大值0
B.在函数y= 2x2中,当x>0时y随x的增大而增大
C.抛物线y=2x2,y=﹣x2,y=﹣中,抛物线y=2x2的开口最小,抛物线y=﹣x2的开口最大
D.不论a是正数还是负数,抛物线y=ax2的顶点都是坐标原点
【详解】
由函数的解析式y=-x2,可知a=-1<0,得到函数的开口向下,有最大值y=0,故A正确;
由函数的解析式y=2x2,可知其对称轴为y轴,对称轴的左边(x<0),y随x增大而减小,对称轴的右边(x>0),y随x增大而增大,故B正确;
根据二次函数的性质,可知系数a决定开口方向和开口大小,且a的绝对值越大,函数图象开口越小,可知抛物线y=2x2的开口最小,抛物线y=-x2的开口第二小,而开口最大,故不正确;不论a是正数还是负数,抛物线y=ax2的顶点都是坐标原点,正确.
故选C.
随堂测试
7 如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=x2与y=–x2的图象,则阴影部分的面积是__________.
【详解】
函数y=x2与y=–x2的图象关于x轴对称,又因正方形的边长为4,以正方形中心为原点建立平面直角坐标系,所以阴影部分的面积为正方形面积的一半,即4×4×=8.
随堂测试
8 在同一直角坐标系中,函数y=ax2(a≠0)与y=ax(a≠0)的大致图象可能是( )
【详解】
∵y=ax(a≠0)的图象是一条经过原点的直线,所以A不正确;
∵当a>0时,y=ax (a≠0)的开口向上,y=ax(a≠0的的图象经过第一,第三象限,当a<0时y=ax (a≠0)的开口向下,y=ax(a≠0)的图象经过第二,第四象限,∴选项B,D不正确,
选项C正确。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
