6.3 反比例函数的应用 课件 (31张PPT)
文档属性
| 名称 | 6.3 反比例函数的应用 课件 (31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 16:58:52 | ||
图片预览









文档简介
(共31张PPT)
北师大版 九年级上册
6.3反比例函数的应用
学习目标
1. 能够通过分析实际问题中变量之间的关系,建立反
比例函数模型解决问题,进一步提高运用函数的图
象、性质的综合能力.
2. 能够根据实际问题确定自变量的取值范围.
情境导入
2.反比例函数图象是什么
1.什么是反比例函数
一般地,形如 (k是常数,k≠0)的函数叫做反比例函数。
y=
k
x
双曲线
情境导入
3.反比例函数 图象有哪些性质
y=
k
x
当k>0,两支曲线分别位于第_______象限;
在每一象限内,y的值随x值的增大而_____。
在每一象限内,y的值随x值的增大而_____;
当k<0,两支曲线分别位于第_______象限。
一、三
减小
二、四
增大
探究新知
核心知识点一:
反比例函数在实际生活中的应用
某校科技小组进行野外考察,利用铺垫若木板的方式通过了一片烂泥湿地.你能解释他们这样做的道理吗?
当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强p(Pa)将如何变化?
探究新知
(1)用含S的代数式表示p,p是S的反比例函数吗?为什么?
如果人和木板对湿地地面的压力合计600N,那么
由p= 得p=
p是S 的反比例函数,因为给定一个S 值,对应的就有唯一的一个p值和它对应,根据函数定义,则p是S 的反比例函数.
探究新知
如果人和木板对湿地地面的压力合计600N,那么
(2)当木板面积为0.2m2时,压强是多少?
当S=0.2m2时,
p= =3000(Pa) .
答:当木板面积为0.2m2时压强是3000Pa.
(3)如果要求压强不超过6000Pa,木板面积至少要多大?
当p=6000Pa时,
S= =0.1( ).
探究新知
如果人和木板对湿地地面的压力合计600N,那么
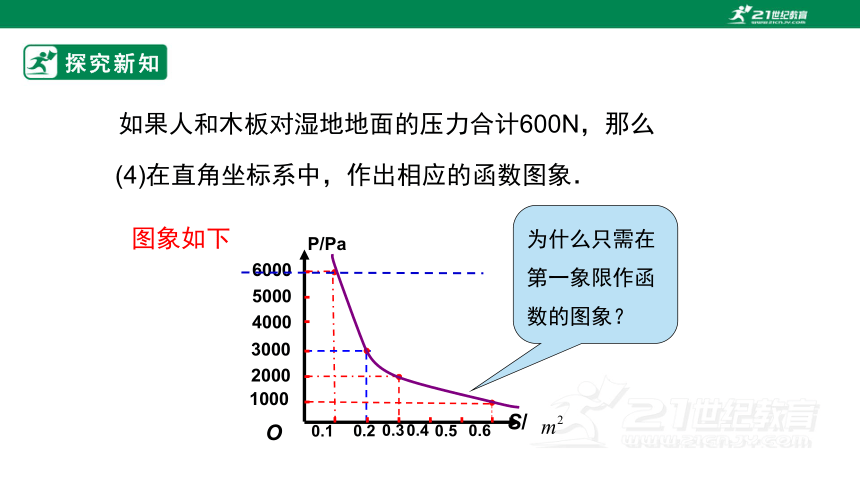
(4)在直角坐标系中,作出相应的函数图象.
图象如下
0.1
0.5
O
0.6
0.3
0.2
0.4
1000
3000
4000
2000
5000
6000
P/Pa
S/
为什么只需在第一象限作函数的图象?
探究新知
如果人和木板对湿地地面的压力合计600N,那么
(5)请利用图象对(2)和(3)作出直观解释,并与同伴交流.
问题(2)是已知图象上的某点的横坐标为0.2,求该点的纵坐标;问题(3)是已知图象上点的纵坐标不大于6000,求这些点所处位置及它们横坐标的取值范围.实际上这些点都在直线p=6000下方的图象上.
探究新知
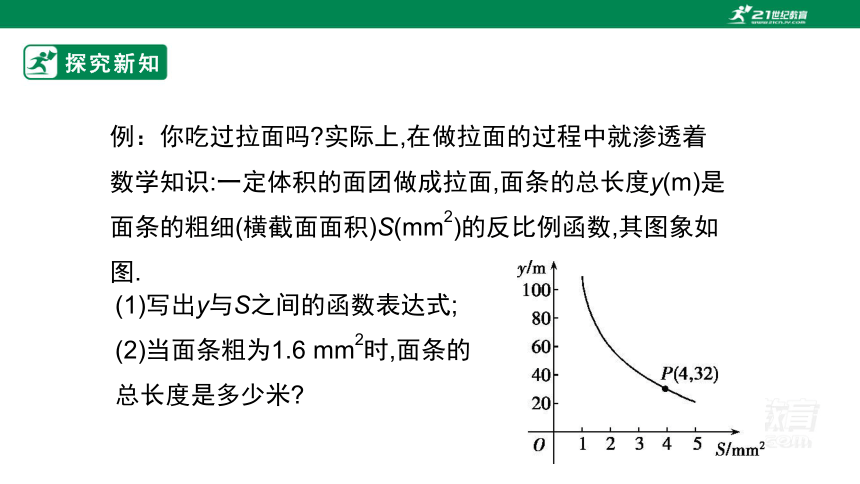
(1)写出y与S之间的函数表达式;
(2)当面条粗为1.6 mm2时,面条的
总长度是多少米
例:你吃过拉面吗 实际上,在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面面积)S(mm2)的反比例函数,其图象如图.
探究新知
解:(1)设y= (k≠0),由图象知双曲线过点P(4,32),可得k=128,故y与S之间的函数表达式为y= (S>0).
(2)当面条粗为1.6 mm2,即S=1.6时,y= =80.因此,当面条粗为1.6 mm2时,面条的总长度为80 m.
探究新知
核心知识点二:
反比例函数在物理问题中的应用
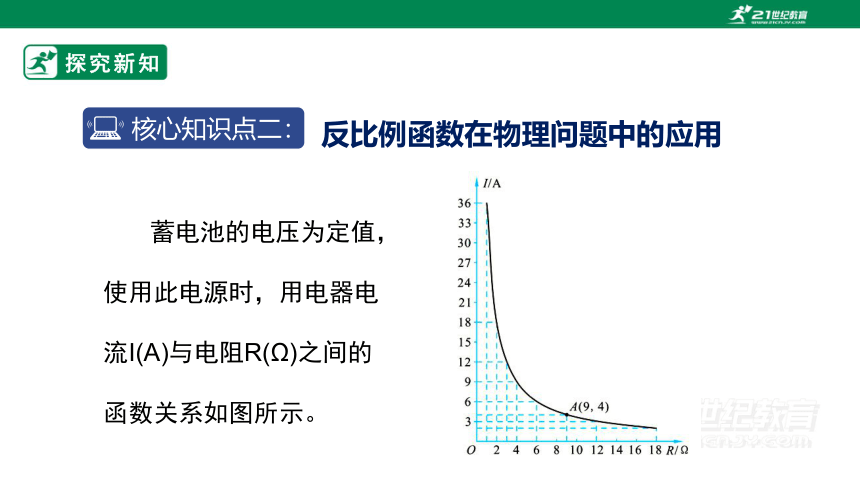
蓄电池的电压为定值,使用此电源时,用电器电流I(A)与电阻R(Ω)之间的函数关系如图所示。
探究新知
(1)蓄电池的电压是多少?你能
答:蓄电池的电压是36V,
写出这一函数的表达式吗?
这一函数的表达式为
I=
36
R
电压=
电流×电阻
=36
I=
36
R
解:
探究新知
(2)如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应该控制在什么范围内?
I≤10
≤10
36
R
R≥3.6(Ω)
解:
答:可变电阻应不小于3.6Ω.
探究新知
核心知识点三:
反比例函数与一次函数综合
如图,正比例函数y=k1x的图象与反比例函数
y= 的图象相交于A,B两点,其中点A的坐标为
( ,2 ).
(1)分别写出这两个函数的表达式.
(2)你能求出点B的坐标吗?你是怎样求的?
探究新知
(2)B点的坐标是两个函数组成的方程组的另一个解.解得x=
所以所求的函数表达式为:y=2x,和
解:(1)把A点坐标分别代入y =k1x,和y =—
解得k1=2.k2=6
x
k2
y=2x
探究新知
归纳总结
1.正比例函数y=k1x与反比例函数y=k2/x
有交点,则k1和k2应满足什么条件?
2.如果正比例函数与反比例函数图象有交点,则交点坐标有什么特点?
正比例函数与反比例函数图象的交点坐标特点关于原点对称.
当k1·k2>0时,有交点;
当k1·k2<0时,没有交点;
探究新知
例1:如图正比例函数,x ( 与反比例函数=(的图像相交于A,B两点其中点A的横坐标为1,当x 时,x 的取值范围是___________________
0<x<1 或 x<-1
探究新知
例2:点A是反比例函数 y= (x>0)的图象上任意一点,AB∥x轴交反比例函数y= 的图象于点B,以AB为边作 ABCD,其中C、D在x轴上,则S ABCD为( )
A、 2 B、3 C、4 D、5
D
随堂练习
1.某地资源总量Q一定,该地人均资源享有量 ̄与人口数n的函数关系图象是( )
A
B
B
D
B
x
随堂练习
2.已知矩形的面积为36cm2,相邻两条边长分别为xcm和ycm,则y与x之间的函数图象大致是( )
A
B
C
D
A
随堂练习
3.如图,A、B、C为反比例函数图像上的三个点,分别从A、B、C向xy轴作垂线,构成三个矩形,它们的面积分别是S1、S2、S3,则S1、S2、S3的大小关系是( )
A:S1=S2>S3
B:S1<S2<S3
C:S1>S2>S3
D:S1=S2=S3
D
随堂练习
4.下列各问题中,两个变量之间的关系不是反比例函数的是( )
A:小明完成100m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的关系。
B:菱形的面积为48cm2,它的两条对角线的长为y(cm)与x(cm)的关系。
C:一个玻璃容器的体积为30L时,所盛液体的质量m与所盛液体的体积V之间的关系。
D:压力为600N时,压强p与受力面积S之间的关系。
C
随堂练习
5.一个水池装水12m3,如果从水管中每小时流出x(m3)的水,经过y(h)可以把水放完,那么y与x的函数关系式是 ,自变量x的取值范围是 .
x>0
6.如图,根据图中提供的信息,可以写出正比例函数的关系式是 ;反比例函数关系式是 。
y=-2x
y=-
随堂练习
7.小丽是一个近视眼,整天眼镜不离鼻子,但自己一直不理解自己眼镜配制的原理,很是苦闷,近来她了解到近视眼镜的度数y(度)与镜片的焦距x(m)成反比例,并请教了师傅了解到自己400度的近视眼镜镜片的焦距为0.2m,可惜她不知道反比例函数的概念,所以她写不出y与x的函数关系式,我们大家正好学过反比例函数了,谁能帮助她解决这个问题呢?
随堂练习
解:设所求反比例函数关系式为
∵当x=0.2时,y=400
∴k=0.2×400=80
因此,反比例函数表达式为
随堂练习
8.某蔬菜生产基地气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线 的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
随堂练习
解:(1)恒温系统在这天保持大棚温度18℃的时间为10小时;
(3)当x=16时,y=13.5,所以当x=16时,大棚内的温度约为13.5℃
∴18= ,∴解得k=216;
(2)∵点B(12,18)在双曲线 上,
课堂小结
实际问题中的反比例函数
过程:
分析实际情境→建立函数模型→明确数学问题
注意:
实际问题中的两个变量往往都只能取非负值;
作实际问题中的函数图像时,横、纵坐标的单位长度不一定相同
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
北师大版 九年级上册
6.3反比例函数的应用
学习目标
1. 能够通过分析实际问题中变量之间的关系,建立反
比例函数模型解决问题,进一步提高运用函数的图
象、性质的综合能力.
2. 能够根据实际问题确定自变量的取值范围.
情境导入
2.反比例函数图象是什么
1.什么是反比例函数
一般地,形如 (k是常数,k≠0)的函数叫做反比例函数。
y=
k
x
双曲线
情境导入
3.反比例函数 图象有哪些性质
y=
k
x
当k>0,两支曲线分别位于第_______象限;
在每一象限内,y的值随x值的增大而_____。
在每一象限内,y的值随x值的增大而_____;
当k<0,两支曲线分别位于第_______象限。
一、三
减小
二、四
增大
探究新知
核心知识点一:
反比例函数在实际生活中的应用
某校科技小组进行野外考察,利用铺垫若木板的方式通过了一片烂泥湿地.你能解释他们这样做的道理吗?
当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强p(Pa)将如何变化?
探究新知
(1)用含S的代数式表示p,p是S的反比例函数吗?为什么?
如果人和木板对湿地地面的压力合计600N,那么
由p= 得p=
p是S 的反比例函数,因为给定一个S 值,对应的就有唯一的一个p值和它对应,根据函数定义,则p是S 的反比例函数.
探究新知
如果人和木板对湿地地面的压力合计600N,那么
(2)当木板面积为0.2m2时,压强是多少?
当S=0.2m2时,
p= =3000(Pa) .
答:当木板面积为0.2m2时压强是3000Pa.
(3)如果要求压强不超过6000Pa,木板面积至少要多大?
当p=6000Pa时,
S= =0.1( ).
探究新知
如果人和木板对湿地地面的压力合计600N,那么
(4)在直角坐标系中,作出相应的函数图象.
图象如下
0.1
0.5
O
0.6
0.3
0.2
0.4
1000
3000
4000
2000
5000
6000
P/Pa
S/
为什么只需在第一象限作函数的图象?
探究新知
如果人和木板对湿地地面的压力合计600N,那么
(5)请利用图象对(2)和(3)作出直观解释,并与同伴交流.
问题(2)是已知图象上的某点的横坐标为0.2,求该点的纵坐标;问题(3)是已知图象上点的纵坐标不大于6000,求这些点所处位置及它们横坐标的取值范围.实际上这些点都在直线p=6000下方的图象上.
探究新知
(1)写出y与S之间的函数表达式;
(2)当面条粗为1.6 mm2时,面条的
总长度是多少米
例:你吃过拉面吗 实际上,在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面面积)S(mm2)的反比例函数,其图象如图.
探究新知
解:(1)设y= (k≠0),由图象知双曲线过点P(4,32),可得k=128,故y与S之间的函数表达式为y= (S>0).
(2)当面条粗为1.6 mm2,即S=1.6时,y= =80.因此,当面条粗为1.6 mm2时,面条的总长度为80 m.
探究新知
核心知识点二:
反比例函数在物理问题中的应用
蓄电池的电压为定值,使用此电源时,用电器电流I(A)与电阻R(Ω)之间的函数关系如图所示。
探究新知
(1)蓄电池的电压是多少?你能
答:蓄电池的电压是36V,
写出这一函数的表达式吗?
这一函数的表达式为
I=
36
R
电压=
电流×电阻
=36
I=
36
R
解:
探究新知
(2)如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应该控制在什么范围内?
I≤10
≤10
36
R
R≥3.6(Ω)
解:
答:可变电阻应不小于3.6Ω.
探究新知
核心知识点三:
反比例函数与一次函数综合
如图,正比例函数y=k1x的图象与反比例函数
y= 的图象相交于A,B两点,其中点A的坐标为
( ,2 ).
(1)分别写出这两个函数的表达式.
(2)你能求出点B的坐标吗?你是怎样求的?
探究新知
(2)B点的坐标是两个函数组成的方程组的另一个解.解得x=
所以所求的函数表达式为:y=2x,和
解:(1)把A点坐标分别代入y =k1x,和y =—
解得k1=2.k2=6
x
k2
y=2x
探究新知
归纳总结
1.正比例函数y=k1x与反比例函数y=k2/x
有交点,则k1和k2应满足什么条件?
2.如果正比例函数与反比例函数图象有交点,则交点坐标有什么特点?
正比例函数与反比例函数图象的交点坐标特点关于原点对称.
当k1·k2>0时,有交点;
当k1·k2<0时,没有交点;
探究新知
例1:如图正比例函数,x ( 与反比例函数=(的图像相交于A,B两点其中点A的横坐标为1,当x 时,x 的取值范围是___________________
0<x<1 或 x<-1
探究新知
例2:点A是反比例函数 y= (x>0)的图象上任意一点,AB∥x轴交反比例函数y= 的图象于点B,以AB为边作 ABCD,其中C、D在x轴上,则S ABCD为( )
A、 2 B、3 C、4 D、5
D
随堂练习
1.某地资源总量Q一定,该地人均资源享有量 ̄与人口数n的函数关系图象是( )
A
B
B
D
B
x
随堂练习
2.已知矩形的面积为36cm2,相邻两条边长分别为xcm和ycm,则y与x之间的函数图象大致是( )
A
B
C
D
A
随堂练习
3.如图,A、B、C为反比例函数图像上的三个点,分别从A、B、C向xy轴作垂线,构成三个矩形,它们的面积分别是S1、S2、S3,则S1、S2、S3的大小关系是( )
A:S1=S2>S3
B:S1<S2<S3
C:S1>S2>S3
D:S1=S2=S3
D
随堂练习
4.下列各问题中,两个变量之间的关系不是反比例函数的是( )
A:小明完成100m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的关系。
B:菱形的面积为48cm2,它的两条对角线的长为y(cm)与x(cm)的关系。
C:一个玻璃容器的体积为30L时,所盛液体的质量m与所盛液体的体积V之间的关系。
D:压力为600N时,压强p与受力面积S之间的关系。
C
随堂练习
5.一个水池装水12m3,如果从水管中每小时流出x(m3)的水,经过y(h)可以把水放完,那么y与x的函数关系式是 ,自变量x的取值范围是 .
x>0
6.如图,根据图中提供的信息,可以写出正比例函数的关系式是 ;反比例函数关系式是 。
y=-2x
y=-
随堂练习
7.小丽是一个近视眼,整天眼镜不离鼻子,但自己一直不理解自己眼镜配制的原理,很是苦闷,近来她了解到近视眼镜的度数y(度)与镜片的焦距x(m)成反比例,并请教了师傅了解到自己400度的近视眼镜镜片的焦距为0.2m,可惜她不知道反比例函数的概念,所以她写不出y与x的函数关系式,我们大家正好学过反比例函数了,谁能帮助她解决这个问题呢?
随堂练习
解:设所求反比例函数关系式为
∵当x=0.2时,y=400
∴k=0.2×400=80
因此,反比例函数表达式为
随堂练习
8.某蔬菜生产基地气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线 的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
随堂练习
解:(1)恒温系统在这天保持大棚温度18℃的时间为10小时;
(3)当x=16时,y=13.5,所以当x=16时,大棚内的温度约为13.5℃
∴18= ,∴解得k=216;
(2)∵点B(12,18)在双曲线 上,
课堂小结
实际问题中的反比例函数
过程:
分析实际情境→建立函数模型→明确数学问题
注意:
实际问题中的两个变量往往都只能取非负值;
作实际问题中的函数图像时,横、纵坐标的单位长度不一定相同
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
