人教版数学九年级上册 22.3 实际问题与二次函数(第3课时)教案
文档属性
| 名称 | 人教版数学九年级上册 22.3 实际问题与二次函数(第3课时)教案 |  | |
| 格式 | docx | ||
| 文件大小 | 477.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 09:20:20 | ||
图片预览


文档简介
22.3 实际问题与二次函数(第3课时)
一、教学目标
【知识与技能】
能根据实际问题构建二次函数模型,并利用函数性质来解决实际问题.
【过程与方法】
再次经历利用二次函数解决实际问题的过程,进一步体验数学建模思想,培养学生解决实际问题的能力.
【情感态度与价值观】
进一步体会数学知识的应用价值,感受数学来自于生活又服务于生活,激发学习数学的兴趣.
二、课型
新授课
三、课时
第3课时,共3课时。
四、教学重难点
【教学重点】
用函数知识解决实际问题,感受数学建模思想.
【教学难点】
根据抛物线型实际问题,建立恰当的平面直角坐标系,建立二次函数模型.
五、课前准备
课件、三角尺、铅笔等.
六、教学过程
(一)导入新课
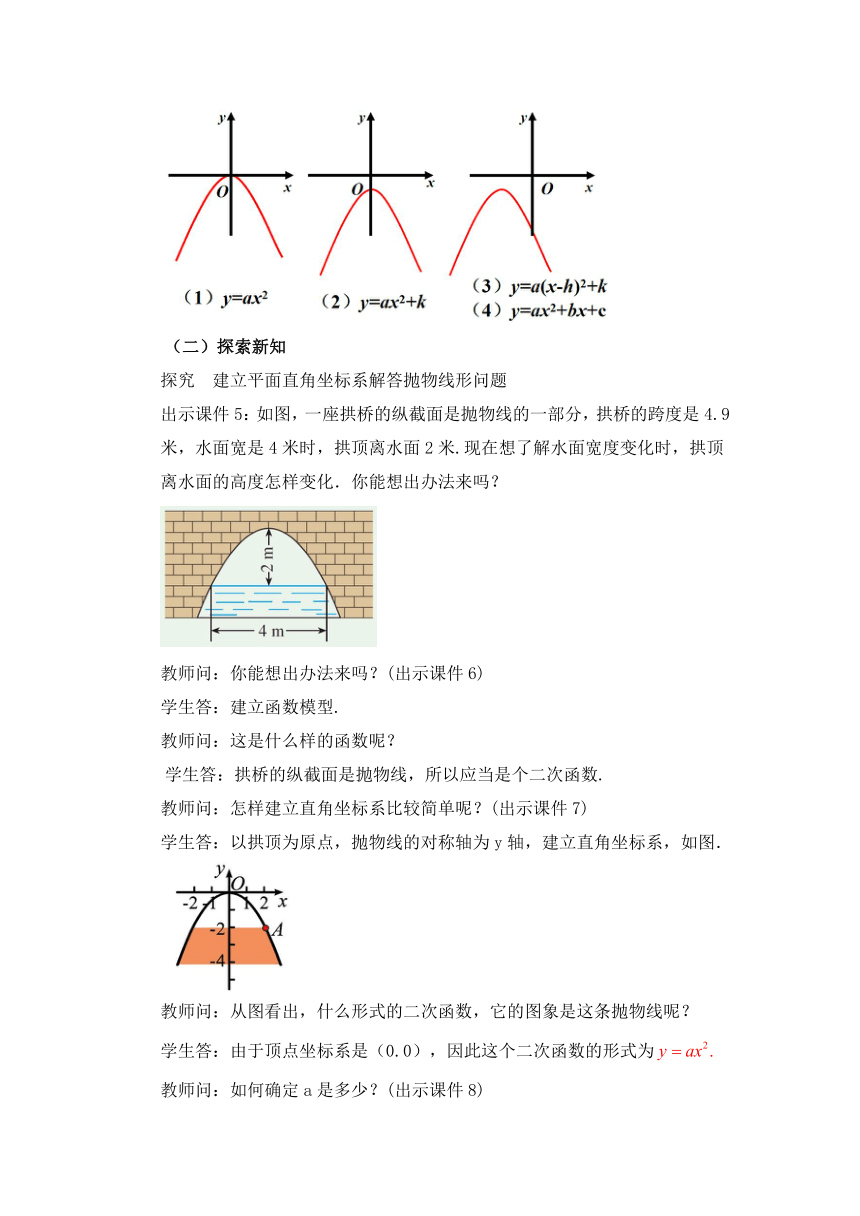
出示课件3:如图是一个二次函数的图象,现在请你根据给出的坐标系的位置,说出这个二次函数的解析式类型.
(二)探索新知
探究 建立平面直角坐标系解答抛物线形问题
出示课件5:如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9米,水面宽是4米时,拱顶离水面2米.现在想了解水面宽度变化时,拱顶离水面的高度怎样变化.你能想出办法来吗?
教师问:你能想出办法来吗?(出示课件6)
学生答:建立函数模型.
教师问:这是什么样的函数呢?
学生答:拱桥的纵截面是抛物线,所以应当是个二次函数.
教师问:怎样建立直角坐标系比较简单呢?(出示课件7)
学生答:以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系,如图.
教师问:从图看出,什么形式的二次函数,它的图象是这条抛物线呢?
学生答:由于顶点坐标系是(0.0),因此这个二次函数的形式为
教师问:如何确定a是多少?(出示课件8)
学生答:已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上,由此得出-2=a×22,解得
因此,,其中|x|是水面宽度的一半,y是拱顶离水面高度的相反数,这样我们就可以了解到水面宽度变化时,拱顶离水面高度怎样变化.
教师问:由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
.
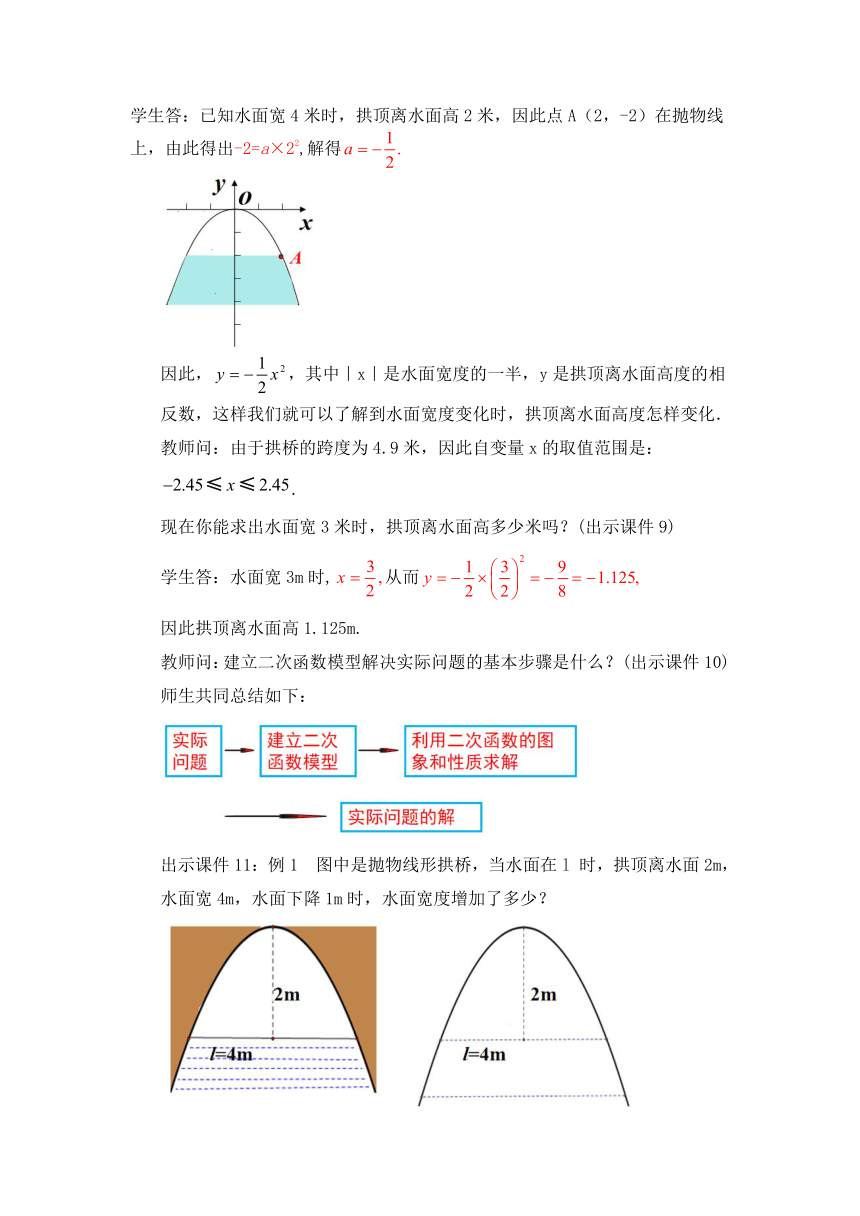
现在你能求出水面宽3米时,拱顶离水面高多少米吗?(出示课件9)
学生答:水面宽3m时,从而
因此拱顶离水面高1.125m.
教师问:建立二次函数模型解决实际问题的基本步骤是什么?(出示课件10)
师生共同总结如下:
出示课件11:例1 图中是抛物线形拱桥,当水面在l 时,拱顶离水面2m,水面宽4m,水面下降1m时,水面宽度增加了多少?
学生独立思考后,师生共同总结如下:(出示课件12,13,14)
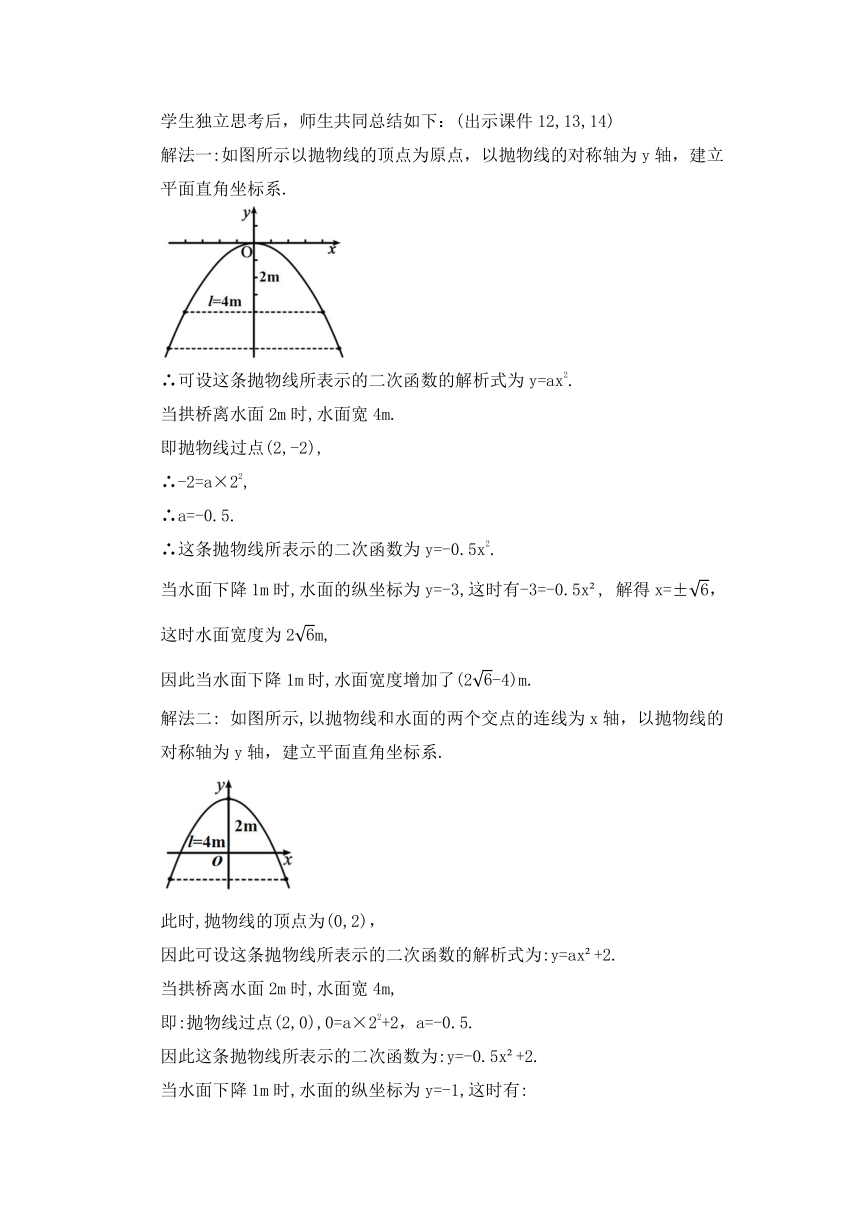
解法一:如图所示以抛物线的顶点为原点,以抛物线的对称轴为y轴,建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为y=ax2.
当拱桥离水面2m时,水面宽4m.
即抛物线过点(2,-2),
∴-2=a×22,
∴a=-0.5.
∴这条抛物线所表示的二次函数为y=-0.5x2.
当水面下降1m时,水面的纵坐标为y=-3,这时有-3=-0.5x , 解得x=±,这时水面宽度为2m,
因此当水面下降1m时,水面宽度增加了(2-4)m.
解法二: 如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.
此时,抛物线的顶点为(0,2),
因此可设这条抛物线所表示的二次函数的解析式为:y=ax +2.
当拱桥离水面2m时,水面宽4m,
即:抛物线过点(2,0),0=a×22+2,a=-0.5.
因此这条抛物线所表示的二次函数为:y=-0.5x +2.
当水面下降1m时,水面的纵坐标为y=-1,这时有:
-1=-0.5x +2解得x=±,这时水面宽度为2m.
因此当水面下降1m时,水面宽度增加了(2-4)m.
解法三:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
此时,抛物线的顶点为(2,2).
因此可设这条抛物线所表示的二次函数的解析式为y=a(x-2) +2.
∵抛物线过点(0,0),
∴0=a×(-2) +2.
∴a=-0.5.
因此这条抛物线所表示的二次函数为y=-0.5(x-2) +2.
当水面下降1m时,水面的纵坐标为y=-1,
这时有-1=-0.5(x-2)2+2,解得x1=2-,x2=2+
这时水面的宽度为x2-x1=2,
因此当水面下降1m时,水面宽度增加了(2-4)m.
出示课件15:回顾“最大利润”和“桥梁建筑”解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.
学生交流后,师生共同总结如下:
1.理解问题;
2.分析问题中的变量和常量,以及它们之间的关系;
3.用数学的方式表示出它们之间的关系;
4.做数学求解;
5.检验结果的合理性.
出示课件16:巩固练习:有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式.
学生思考后自主解答.
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04.
∴y=-0.04x2 .
出示课件18:如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
学生自主思考后,师生共同解决如下.
出示课件19:解:如图,建立直角坐标系.
则点A的坐标是(1.5,3.05),篮球在最大高度
时的位置为B(0,3.5).
以点C表示运动员投篮球的出手处.
设以y轴为对称轴的抛物线的解析式为y=a(x-0)2+k,即y=ax2+k.而点A,B在这条抛物线上,所以有
所以该抛物线的表达式为y=﹣0.2x2+3.5.
当x=﹣2.5时,y=2.25.
故该运动员出手时的高度为2.25m.
出示课件20:巩固练习:
一名同学推铅球,铅球出手后行进过程中离地面的高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=x2+x+c,其图象如图所示.已知铅球落地时的水平距离为10m.
(1)求铅球出手时离地面的高度;
(2)在铅球行进过程中,当它离地面的高度为m时,求此时铅球
的水平距离.
学生自主思考后板演如下:
解:(1)根据题意,将(10,0)代入y=x2+x+c,
得×102+×10+c=0,
解得c=,
即铅球出手时离地面的高度m;
(2)将y=代入x2+x+=, ,
整理,得x2﹣8x﹣9=0,
解得x1=9,x2=﹣1(舍),
∴此时铅球的水平距离为9m.
(三)课堂练习(出示课件22-30)
1.某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.
2.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在 s后落地.
3.如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为,那么铅球运动过程中
最高点离地面的距离为 米.
4.某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
A.50m B.100m
C.160m D.200m
5.某工厂要赶制一批抗震救灾用的大型活动板房.如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为5.6m.
(1)在如图所示的平面直角坐标系中,求抛物线的表达式.
(2)现需在抛物线AOB的区域内安装几扇窗户,窗户的底边在AB上,每扇窗户宽1.5m,高1.6m,相邻窗户之间的间距均为0.8m,左右两边窗户的窗角所在的点到抛物线的水平距离至少为0.8m.请计算最多可安装几扇这样的窗户?
6.悬索桥两端主塔塔顶之间的主悬钢索,其形状可近似地看作抛物线,水平桥面与主悬钢索之间用垂直钢索连接.已知两端主塔之间的水平距离为900 m,两主塔塔顶距桥面的高度为81.5 m,主悬钢索最低点离桥面的高度为0.5 m.
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图所示,求这条抛物线对应的函数表达式;
(2)计算距离桥两端主塔分别为100m,50m处垂直钢索的长.
参考答案:
1.解:(1)设水柱所在抛物线(第一象限部分)的函数表达式为y=a(x﹣3)2+5(a≠0),将(8,0)代入y=a(x﹣3)2+5,得25a+5=0,解得a=﹣0.2,
∴水柱所在抛物线(第一象限部分)的函数表达式为y=﹣0.2(x﹣3)2+5(0<x<8).
(2)当y=1.8时,有﹣0.2(x﹣3)2+5=1.8,解得:x1=﹣1,x2=7,
因此为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心7米以内.
(3)当x=0时,y=﹣0.2(x﹣3)2+5=3.2.
设改造后水柱所在抛物线(第一象限部分)的函数表达式为y=﹣0.2x2+bx+3.2,
∵该函数图象过点(16,0),
∴0=﹣0.2×162+16b+3.2,解得b=3.
∴改造后水柱所在抛物线(第一象限部分)的函数表达式为y=﹣0.2x2+3x+3.2=﹣0.2(x﹣7.5)2+14.45.
∴扩建改造后喷水池水柱的最大高度为14.45米.
2.4
3.2
4.C
5.解:(1)设抛物线的表达式为y=ax2.
∵点B(6,﹣5.6)在抛物线的图象上,
∴﹣5.6=36a,
∴抛物线的表达式为
(2)设窗户上边所在直线交抛物线于C,D两点,D点坐标为(k,t),已知窗户高1.6m,
∴t=﹣5.6﹣(﹣1.6)=﹣4.
∴,解得k=,
即k1≈5.07,k2≈﹣5.07.
∴CD=5.07×2≈10.14(m).
设最多可安装n扇窗户,
∴1.5n+0.8(n﹣1)+0.8×2≤10.14,解得n≤4.06.
则最大的正整数为4.
答:最多可安装4扇窗户.
6.解:根据题意,得抛物线的顶点坐标为(0,0.5),
对称轴为y轴,设抛物线的函数表达式为y=ax2+0.5.
抛物线经过点(450,81.5),代入上式,得
81.5=a 4502+0.5.
解得
故所求表达式为
(2)当x=450﹣100=350(m)时,得
当x=450﹣50=400(m)时,得
(四)课堂小结
通过本节课的学习,你有什么收获?
(五)课前预习
预习下节课(23.1第1课时)的相关内容.
七、课后作业
配套练习册内容
八、板书设计:
九、教学反思:
本课时教学与上一课时基本相同,所不同的是教学时应注意建立正确的直角坐标系,使类似于抛物线的实际问题转化为平面直角坐标系中的抛物线.教学时教师仍可采用分步设问的形式让学生回答并让学生相互交流.教师应鼓励学生用多种方法建立平面直角坐标系,并求出相应抛物线表达式,在这一过程中让学生体验探究发现的快乐,体会数学的最优化思考.
一、教学目标
【知识与技能】
能根据实际问题构建二次函数模型,并利用函数性质来解决实际问题.
【过程与方法】
再次经历利用二次函数解决实际问题的过程,进一步体验数学建模思想,培养学生解决实际问题的能力.
【情感态度与价值观】
进一步体会数学知识的应用价值,感受数学来自于生活又服务于生活,激发学习数学的兴趣.
二、课型
新授课
三、课时
第3课时,共3课时。
四、教学重难点
【教学重点】
用函数知识解决实际问题,感受数学建模思想.
【教学难点】
根据抛物线型实际问题,建立恰当的平面直角坐标系,建立二次函数模型.
五、课前准备
课件、三角尺、铅笔等.
六、教学过程
(一)导入新课
出示课件3:如图是一个二次函数的图象,现在请你根据给出的坐标系的位置,说出这个二次函数的解析式类型.
(二)探索新知
探究 建立平面直角坐标系解答抛物线形问题
出示课件5:如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9米,水面宽是4米时,拱顶离水面2米.现在想了解水面宽度变化时,拱顶离水面的高度怎样变化.你能想出办法来吗?
教师问:你能想出办法来吗?(出示课件6)
学生答:建立函数模型.
教师问:这是什么样的函数呢?
学生答:拱桥的纵截面是抛物线,所以应当是个二次函数.
教师问:怎样建立直角坐标系比较简单呢?(出示课件7)
学生答:以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系,如图.
教师问:从图看出,什么形式的二次函数,它的图象是这条抛物线呢?
学生答:由于顶点坐标系是(0.0),因此这个二次函数的形式为
教师问:如何确定a是多少?(出示课件8)
学生答:已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上,由此得出-2=a×22,解得
因此,,其中|x|是水面宽度的一半,y是拱顶离水面高度的相反数,这样我们就可以了解到水面宽度变化时,拱顶离水面高度怎样变化.
教师问:由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
.
现在你能求出水面宽3米时,拱顶离水面高多少米吗?(出示课件9)
学生答:水面宽3m时,从而
因此拱顶离水面高1.125m.
教师问:建立二次函数模型解决实际问题的基本步骤是什么?(出示课件10)
师生共同总结如下:
出示课件11:例1 图中是抛物线形拱桥,当水面在l 时,拱顶离水面2m,水面宽4m,水面下降1m时,水面宽度增加了多少?
学生独立思考后,师生共同总结如下:(出示课件12,13,14)
解法一:如图所示以抛物线的顶点为原点,以抛物线的对称轴为y轴,建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为y=ax2.
当拱桥离水面2m时,水面宽4m.
即抛物线过点(2,-2),
∴-2=a×22,
∴a=-0.5.
∴这条抛物线所表示的二次函数为y=-0.5x2.
当水面下降1m时,水面的纵坐标为y=-3,这时有-3=-0.5x , 解得x=±,这时水面宽度为2m,
因此当水面下降1m时,水面宽度增加了(2-4)m.
解法二: 如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.
此时,抛物线的顶点为(0,2),
因此可设这条抛物线所表示的二次函数的解析式为:y=ax +2.
当拱桥离水面2m时,水面宽4m,
即:抛物线过点(2,0),0=a×22+2,a=-0.5.
因此这条抛物线所表示的二次函数为:y=-0.5x +2.
当水面下降1m时,水面的纵坐标为y=-1,这时有:
-1=-0.5x +2解得x=±,这时水面宽度为2m.
因此当水面下降1m时,水面宽度增加了(2-4)m.
解法三:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
此时,抛物线的顶点为(2,2).
因此可设这条抛物线所表示的二次函数的解析式为y=a(x-2) +2.
∵抛物线过点(0,0),
∴0=a×(-2) +2.
∴a=-0.5.
因此这条抛物线所表示的二次函数为y=-0.5(x-2) +2.
当水面下降1m时,水面的纵坐标为y=-1,
这时有-1=-0.5(x-2)2+2,解得x1=2-,x2=2+
这时水面的宽度为x2-x1=2,
因此当水面下降1m时,水面宽度增加了(2-4)m.
出示课件15:回顾“最大利润”和“桥梁建筑”解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.
学生交流后,师生共同总结如下:
1.理解问题;
2.分析问题中的变量和常量,以及它们之间的关系;
3.用数学的方式表示出它们之间的关系;
4.做数学求解;
5.检验结果的合理性.
出示课件16:巩固练习:有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式.
学生思考后自主解答.
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04.
∴y=-0.04x2 .
出示课件18:如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
学生自主思考后,师生共同解决如下.
出示课件19:解:如图,建立直角坐标系.
则点A的坐标是(1.5,3.05),篮球在最大高度
时的位置为B(0,3.5).
以点C表示运动员投篮球的出手处.
设以y轴为对称轴的抛物线的解析式为y=a(x-0)2+k,即y=ax2+k.而点A,B在这条抛物线上,所以有
所以该抛物线的表达式为y=﹣0.2x2+3.5.
当x=﹣2.5时,y=2.25.
故该运动员出手时的高度为2.25m.
出示课件20:巩固练习:
一名同学推铅球,铅球出手后行进过程中离地面的高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=x2+x+c,其图象如图所示.已知铅球落地时的水平距离为10m.
(1)求铅球出手时离地面的高度;
(2)在铅球行进过程中,当它离地面的高度为m时,求此时铅球
的水平距离.
学生自主思考后板演如下:
解:(1)根据题意,将(10,0)代入y=x2+x+c,
得×102+×10+c=0,
解得c=,
即铅球出手时离地面的高度m;
(2)将y=代入x2+x+=, ,
整理,得x2﹣8x﹣9=0,
解得x1=9,x2=﹣1(舍),
∴此时铅球的水平距离为9m.
(三)课堂练习(出示课件22-30)
1.某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.
2.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在 s后落地.
3.如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为,那么铅球运动过程中
最高点离地面的距离为 米.
4.某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
A.50m B.100m
C.160m D.200m
5.某工厂要赶制一批抗震救灾用的大型活动板房.如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为5.6m.
(1)在如图所示的平面直角坐标系中,求抛物线的表达式.
(2)现需在抛物线AOB的区域内安装几扇窗户,窗户的底边在AB上,每扇窗户宽1.5m,高1.6m,相邻窗户之间的间距均为0.8m,左右两边窗户的窗角所在的点到抛物线的水平距离至少为0.8m.请计算最多可安装几扇这样的窗户?
6.悬索桥两端主塔塔顶之间的主悬钢索,其形状可近似地看作抛物线,水平桥面与主悬钢索之间用垂直钢索连接.已知两端主塔之间的水平距离为900 m,两主塔塔顶距桥面的高度为81.5 m,主悬钢索最低点离桥面的高度为0.5 m.
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图所示,求这条抛物线对应的函数表达式;
(2)计算距离桥两端主塔分别为100m,50m处垂直钢索的长.
参考答案:
1.解:(1)设水柱所在抛物线(第一象限部分)的函数表达式为y=a(x﹣3)2+5(a≠0),将(8,0)代入y=a(x﹣3)2+5,得25a+5=0,解得a=﹣0.2,
∴水柱所在抛物线(第一象限部分)的函数表达式为y=﹣0.2(x﹣3)2+5(0<x<8).
(2)当y=1.8时,有﹣0.2(x﹣3)2+5=1.8,解得:x1=﹣1,x2=7,
因此为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心7米以内.
(3)当x=0时,y=﹣0.2(x﹣3)2+5=3.2.
设改造后水柱所在抛物线(第一象限部分)的函数表达式为y=﹣0.2x2+bx+3.2,
∵该函数图象过点(16,0),
∴0=﹣0.2×162+16b+3.2,解得b=3.
∴改造后水柱所在抛物线(第一象限部分)的函数表达式为y=﹣0.2x2+3x+3.2=﹣0.2(x﹣7.5)2+14.45.
∴扩建改造后喷水池水柱的最大高度为14.45米.
2.4
3.2
4.C
5.解:(1)设抛物线的表达式为y=ax2.
∵点B(6,﹣5.6)在抛物线的图象上,
∴﹣5.6=36a,
∴抛物线的表达式为
(2)设窗户上边所在直线交抛物线于C,D两点,D点坐标为(k,t),已知窗户高1.6m,
∴t=﹣5.6﹣(﹣1.6)=﹣4.
∴,解得k=,
即k1≈5.07,k2≈﹣5.07.
∴CD=5.07×2≈10.14(m).
设最多可安装n扇窗户,
∴1.5n+0.8(n﹣1)+0.8×2≤10.14,解得n≤4.06.
则最大的正整数为4.
答:最多可安装4扇窗户.
6.解:根据题意,得抛物线的顶点坐标为(0,0.5),
对称轴为y轴,设抛物线的函数表达式为y=ax2+0.5.
抛物线经过点(450,81.5),代入上式,得
81.5=a 4502+0.5.
解得
故所求表达式为
(2)当x=450﹣100=350(m)时,得
当x=450﹣50=400(m)时,得
(四)课堂小结
通过本节课的学习,你有什么收获?
(五)课前预习
预习下节课(23.1第1课时)的相关内容.
七、课后作业
配套练习册内容
八、板书设计:
九、教学反思:
本课时教学与上一课时基本相同,所不同的是教学时应注意建立正确的直角坐标系,使类似于抛物线的实际问题转化为平面直角坐标系中的抛物线.教学时教师仍可采用分步设问的形式让学生回答并让学生相互交流.教师应鼓励学生用多种方法建立平面直角坐标系,并求出相应抛物线表达式,在这一过程中让学生体验探究发现的快乐,体会数学的最优化思考.
同课章节目录
