青岛版数学八年级上册 2.6等腰三角形第3课时 课件(共17张PPT)
文档属性
| 名称 | 青岛版数学八年级上册 2.6等腰三角形第3课时 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 679.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 09:36:54 | ||
图片预览




文档简介
(共17张PPT)
2.6 等腰三角形
第3课时
这就是今天我们要学的等边三角形.
你发现了什么?
1.理解并掌握等边三角形的定义,探索等边三角形的性
质和判定方法.
2.能够用等边三角形的知识解决相应的数学问题.
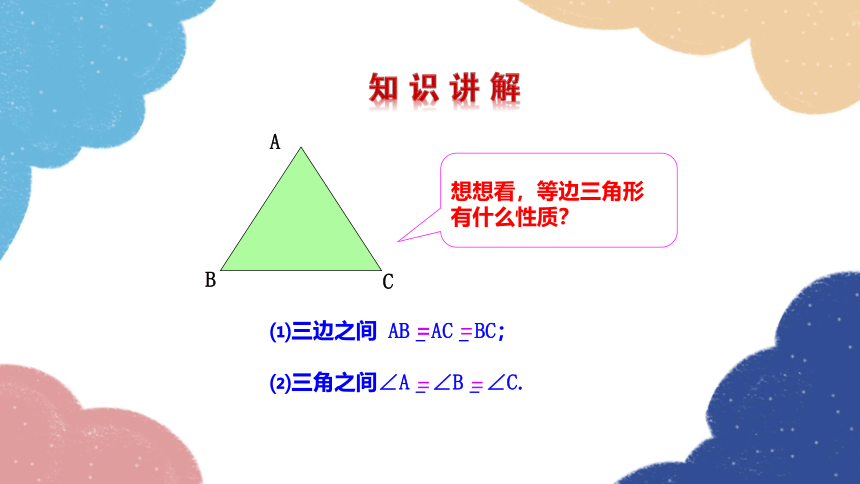
想想看,等边三角形
有什么性质?
A
B
C
⑴三边之间 AB_AC_BC;
⑵三角之间∠A_∠B_∠C.
=
=
=
=
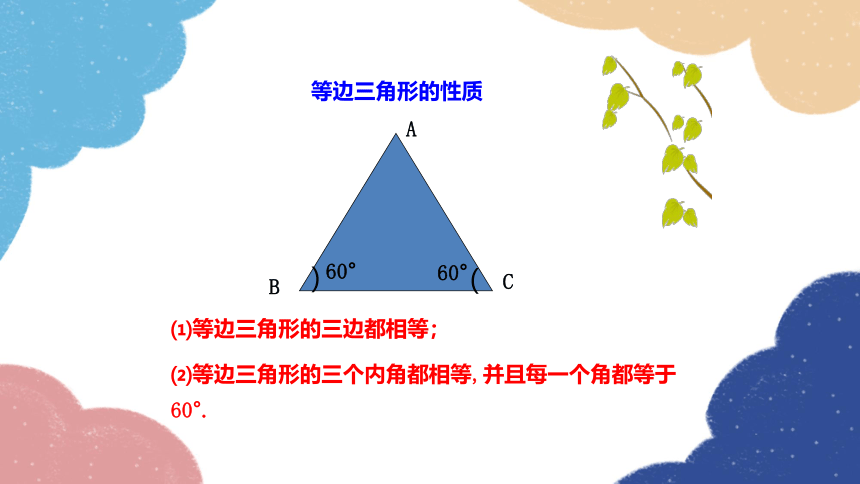
⑵等边三角形的三个内角都相等,并且每一个角都等于60°.
⑴等边三角形的三边都相等;
A
B
C
)
(
60°
60°
等边三角形的性质
等边三角形性质探索:
等边三角形是轴对称图形吗?若是,有几条对称轴?
结论:等边三角形是轴对称图形,有三条对称轴
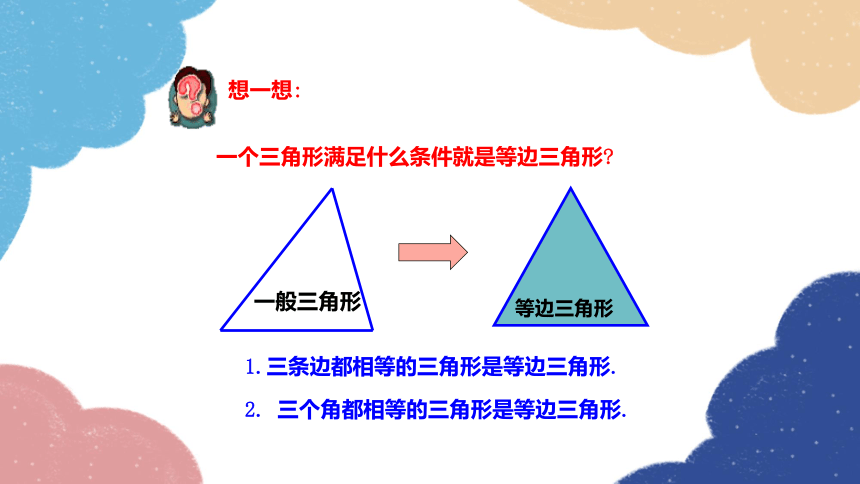
一个三角形满足什么条件就是等边三角形
想一想:
一般三角形
1.三条边都相等的三角形是等边三角形.
2. 三个角都相等的三角形是等边三角形.
等边三角形
有一个角是60°的等腰三角形是等边三角形.
等腰三角形
等边三角形
等腰三角形满足什么条件时是等边三角形呢
问题 已知,在△ABC 中,∠A =60°,( ).
请你在括号内补充一个条件,使△ABC 能成为等边三角
形.
∠B =60°(或∠C =60°)
AB =BC、AC =BC、AB =BC =AC
A
B
C
如图,△ABC 是等边三角形,若点D、E 在边AB、AC 的反向
延长线上,且DE∥BC,求证:△ADE 是等边三角形.
【证明】 ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.
A
D
E
B
C
【例题】
3.已知△ABC中,∠A=∠B=60°,AB=3cm ,则△ABC的周长____.
9
4.△ABC是等腰三角形,周长为15cm且∠A=60°,则BC=_______
5
1.三边都相等的三角形叫做____三角形.
2.等边三角形的每个内角都等于____度.
60
等边
【跟踪训练】
1.三条边都相等的三角形是等边三角形.
2.三个角都相等的三角形是等边三角形.
3.有一个角是60°的等腰三角形是等边三角形.
等边三角形的判定
通过本课时的学习,需要我们掌握:
A
N
l
1.(宿迁·中考)数学活动课上,老师在黑板上画直线l
平行于射线AN(如图),让同学们在直线和射线上各找一
点B和C,使得以A,B,C为顶点的三角形是等腰直角三角
形.这样的三角形最多能画______个.
【解析】分别以A,B,C为直角顶点,则共有3个等腰直角
三角形.
答案:3
2.如图,在等边△ABC中,点D是BC边的中点,以AD为边作
等边△ADE,则∠CAE= .
【解析】点D是等边△ABC中BC边的中点,故∠DAC=30°;
在等边△ADE中,∠CAE=60°-30°=30°.
答案:30°
A
B
C
D
E
【解析】∵ΔABC是等边三角形,
∴∠ABC=∠ACB=60°,AB=BC,
∵BD为中线,∴∠DBC=30°,∵CE=CD,
∴∠E=∠CDE,∠E+∠CDE=∠ACB=60°,
∴∠E=30°,∴∠E=∠DBC,∴DE=BD=6㎝.
3.如图,已知,△ABC是等边三角形,BD是中线,BD=6,延长BC到E。使CE=CD,求DE长。
【证明】∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
AB=AC=BC,∵AD=BE=CF,即BD=CE=AF,
在△AFD,△BDE和△CEF中,
∠A=∠B=∠C=60°,
AD=BE=CF
AF=BD=CE
∴△AFD≌△BDE≌△CEF
∴DF=DE=EF,∴△DEF是等边三角形
4.如图,D、E、F分别是等边三角形ABC三边上三点,
且AD=BE=CF。试问:△DEF是什么三角形?
A
B
C
D
E
F
谢 谢
2.6 等腰三角形
第3课时
这就是今天我们要学的等边三角形.
你发现了什么?
1.理解并掌握等边三角形的定义,探索等边三角形的性
质和判定方法.
2.能够用等边三角形的知识解决相应的数学问题.
想想看,等边三角形
有什么性质?
A
B
C
⑴三边之间 AB_AC_BC;
⑵三角之间∠A_∠B_∠C.
=
=
=
=
⑵等边三角形的三个内角都相等,并且每一个角都等于60°.
⑴等边三角形的三边都相等;
A
B
C
)
(
60°
60°
等边三角形的性质
等边三角形性质探索:
等边三角形是轴对称图形吗?若是,有几条对称轴?
结论:等边三角形是轴对称图形,有三条对称轴
一个三角形满足什么条件就是等边三角形
想一想:
一般三角形
1.三条边都相等的三角形是等边三角形.
2. 三个角都相等的三角形是等边三角形.
等边三角形
有一个角是60°的等腰三角形是等边三角形.
等腰三角形
等边三角形
等腰三角形满足什么条件时是等边三角形呢
问题 已知,在△ABC 中,∠A =60°,( ).
请你在括号内补充一个条件,使△ABC 能成为等边三角
形.
∠B =60°(或∠C =60°)
AB =BC、AC =BC、AB =BC =AC
A
B
C
如图,△ABC 是等边三角形,若点D、E 在边AB、AC 的反向
延长线上,且DE∥BC,求证:△ADE 是等边三角形.
【证明】 ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.
A
D
E
B
C
【例题】
3.已知△ABC中,∠A=∠B=60°,AB=3cm ,则△ABC的周长____.
9
4.△ABC是等腰三角形,周长为15cm且∠A=60°,则BC=_______
5
1.三边都相等的三角形叫做____三角形.
2.等边三角形的每个内角都等于____度.
60
等边
【跟踪训练】
1.三条边都相等的三角形是等边三角形.
2.三个角都相等的三角形是等边三角形.
3.有一个角是60°的等腰三角形是等边三角形.
等边三角形的判定
通过本课时的学习,需要我们掌握:
A
N
l
1.(宿迁·中考)数学活动课上,老师在黑板上画直线l
平行于射线AN(如图),让同学们在直线和射线上各找一
点B和C,使得以A,B,C为顶点的三角形是等腰直角三角
形.这样的三角形最多能画______个.
【解析】分别以A,B,C为直角顶点,则共有3个等腰直角
三角形.
答案:3
2.如图,在等边△ABC中,点D是BC边的中点,以AD为边作
等边△ADE,则∠CAE= .
【解析】点D是等边△ABC中BC边的中点,故∠DAC=30°;
在等边△ADE中,∠CAE=60°-30°=30°.
答案:30°
A
B
C
D
E
【解析】∵ΔABC是等边三角形,
∴∠ABC=∠ACB=60°,AB=BC,
∵BD为中线,∴∠DBC=30°,∵CE=CD,
∴∠E=∠CDE,∠E+∠CDE=∠ACB=60°,
∴∠E=30°,∴∠E=∠DBC,∴DE=BD=6㎝.
3.如图,已知,△ABC是等边三角形,BD是中线,BD=6,延长BC到E。使CE=CD,求DE长。
【证明】∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
AB=AC=BC,∵AD=BE=CF,即BD=CE=AF,
在△AFD,△BDE和△CEF中,
∠A=∠B=∠C=60°,
AD=BE=CF
AF=BD=CE
∴△AFD≌△BDE≌△CEF
∴DF=DE=EF,∴△DEF是等边三角形
4.如图,D、E、F分别是等边三角形ABC三边上三点,
且AD=BE=CF。试问:△DEF是什么三角形?
A
B
C
D
E
F
谢 谢
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
