人教版七年级上册3.1.2等式的性质课件(共28张PPT)
文档属性
| 名称 | 人教版七年级上册3.1.2等式的性质课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
第三章 一元一次方程
3.1 从算式到方程
3.1.2 等式的性质
学习目标
1.利用天平,通过观察、分析得出等式的两条重要性质。2.会利用等式的两条性质解方程。
重点
探索等式的性质
难点
掌握等式的性质及注意事项。
√
√
√
√
√
下列各式中哪些是等式?
; ; ;④ 9x+10=19;
;⑥2+3=5;⑦3×4=12;⑧360;
; .
用等号表示相等关系的式子叫做等式.
我们可以用a=b表示一般的等式.
复习回顾
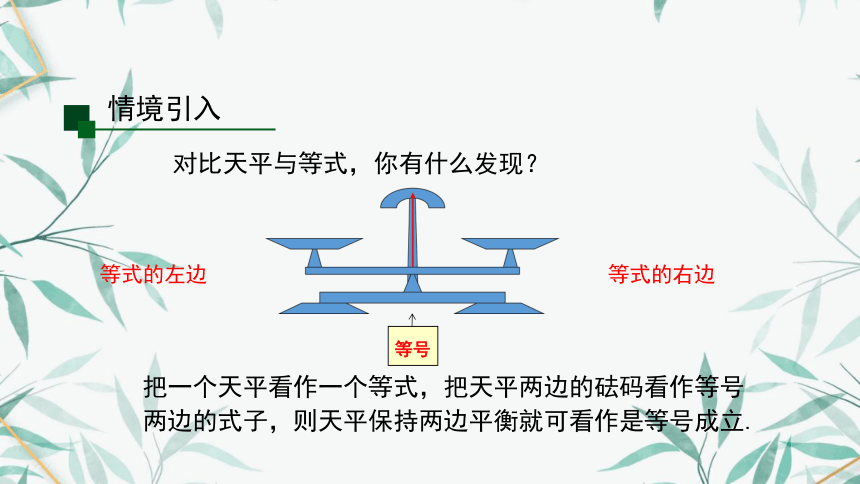
对比天平与等式,你有什么发现?
把一个天平看作一个等式,把天平两边的砝码看作等号两边的式子,则天平保持两边平衡就可看作是等号成立.
等号
等式的左边
等式的右边
情境引入
观察天平有什么特性?
天平两边同时加入相同质量的砝码
天平仍然平衡
天平两边同时拿去相同质量的砝码
天平仍然平衡
学习新知
观察与思考
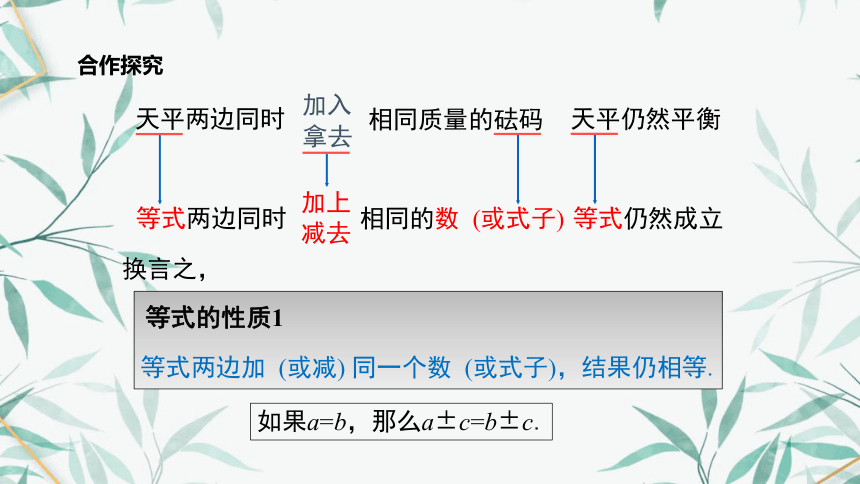
天平两边同时
天平仍然平衡
加入
拿去
相同质量的砝码
相同的数 (或式子)
等式两边同时
加上
减去
等式仍然成立
换言之,
等式两边加 (或减) 同一个数 (或式子),结果仍相等.
如果a=b,那么a±c=b±c.
等式的性质1
合作探究
例1 根据等式性质填空
(1)如果a=2,那么a+3=2______.
依据是等式的性质____,在等式的两边都____________________;
加同一个数,结果仍相等
+3
1
例题讲解
例1 根据等式性质填空
(2)如果a=2, 那么a-5=2______.
依据是等式的性质____,在等式的两边都____________________;
减同一个数,结果仍相等
-5
1
由天平看等式的性质2
你能发现什么规律?
等式两边乘同一个数,或除以同一个不为0的数,结
果仍相等.
等式的性质2
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
例2 根据等式性质填空
(1)如果a=2,那么-3a=2________,
依据是等式的性质____,在等式的两边都____________________;
乘同一个数,结果仍相等
×(-3)
2
例2 根据等式性质填空
(2)如果a=2,那么 ,
依据是等式的性质____,在等式的两边都____________________
________________.
2
除以同一个不为0的数,
结果仍相等
等式的性质1:
如果a=b,那么a±c=b±c.
等式的性质2:
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
等式两边加(或减)同一个数(或式子),结果仍相等.
注意:
1. 等式两边都要参加运算,并且是作同一种运算.
2. 等式两边都不能除以0,即0不能作除数或分母.
例3. 用适当的数或式子填空,并说明是根据等式的哪一条性质以及怎样变形.
(1)因为
等式性质1
4
等式性质2
3
3
例3. 用适当的数或式子填空,并说明是根据等式的哪一条性质以及怎样变形.
(2)因为
2x
3
等式性质1
等式性质2
练习 已知 3a-2=7a-2 以下是某同学的变形过程,请找出变形过程中的错误并解答.
解:两边加2,得 3a-2+2=7a-2+2.
化简,得 3a=7a.
两边除以a,得 3=7.
反思:
等式两边都要参加运算,并且是同一种运算
等式两边都不能除以0,即0不能做除数或分母
例4 . 利用等式的性质解下列方程
(1)x+7=26
解:(1)两边减7,得
x = 19
于是
x+7-7=26-7
(2)-5x=20 (3)
解:(2)两边除以-5,得
于是
x = -4
(3)两边加5,得
化简,得
两边乘-3,得
x = -27
解以x为未知数的方程,就是把方程逐步转化为x=a(常数)的形式,等式的性质是转化的重要依据.
一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等. 例如,
将x = -27代入方程 的左边,得
方程的左右两边相等,所以x = -27是方程 的解.
A
2. 下列各式变形正确的是 ( )
A. 由3x-1= 2x+1得3x-2x =1+1
B. 由5+1= 6得5= 6+1
C. 由2(x+1) = 2y+1得x +1= y +1
D. 由2a + 3b = c-6 得2a = c-18b
1. 下列说法正确的是_______
A. 等式都是方程
B. 方程都是等式
C. 不是方程的就不是等式
D. 未知数的值就是方程的解
B
巩固练习
3. 下列变形,正确的是 ( )
A. 若ac = bc,则a = b
B. 若 ,则a = b
C. 若a2 = b2,则a = b
D. 若 ,则x = -2
B
4.用等式的性质解下列方程并检验:
(1)x-5=6; (2)0.3x=45;(3)5x+4=0.
解: (1)两边加5,得 x-5+5=6+5.
于是 x=11.
检验: 当x=11时,左边=11-5=6=右边,
所以x=11是原方程的解.
(2)两边除以0.3,得 .
于是 x=150.
检验:当x=150时,左边=0.3×150=45=右边,
所以x=150是原方程的解.
(3)两边减4,得 5x+4-4=0-4.
化简,得 5x=-4.
两边除以5,得 x= .
检验:当x= 时,左边=0=右边,
所以x= 是原方程的解.
课堂小结
等式性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
如果a=b,那么a±c=b±c.
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,
结果仍相等.
课下作业
必做:课本83页习题3.1第4题;
选做:智慧学习103页学习巩固。
第三章 一元一次方程
3.1 从算式到方程
3.1.2 等式的性质
学习目标
1.利用天平,通过观察、分析得出等式的两条重要性质。2.会利用等式的两条性质解方程。
重点
探索等式的性质
难点
掌握等式的性质及注意事项。
√
√
√
√
√
下列各式中哪些是等式?
; ; ;④ 9x+10=19;
;⑥2+3=5;⑦3×4=12;⑧360;
; .
用等号表示相等关系的式子叫做等式.
我们可以用a=b表示一般的等式.
复习回顾
对比天平与等式,你有什么发现?
把一个天平看作一个等式,把天平两边的砝码看作等号两边的式子,则天平保持两边平衡就可看作是等号成立.
等号
等式的左边
等式的右边
情境引入
观察天平有什么特性?
天平两边同时加入相同质量的砝码
天平仍然平衡
天平两边同时拿去相同质量的砝码
天平仍然平衡
学习新知
观察与思考
天平两边同时
天平仍然平衡
加入
拿去
相同质量的砝码
相同的数 (或式子)
等式两边同时
加上
减去
等式仍然成立
换言之,
等式两边加 (或减) 同一个数 (或式子),结果仍相等.
如果a=b,那么a±c=b±c.
等式的性质1
合作探究
例1 根据等式性质填空
(1)如果a=2,那么a+3=2______.
依据是等式的性质____,在等式的两边都____________________;
加同一个数,结果仍相等
+3
1
例题讲解
例1 根据等式性质填空
(2)如果a=2, 那么a-5=2______.
依据是等式的性质____,在等式的两边都____________________;
减同一个数,结果仍相等
-5
1
由天平看等式的性质2
你能发现什么规律?
等式两边乘同一个数,或除以同一个不为0的数,结
果仍相等.
等式的性质2
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
例2 根据等式性质填空
(1)如果a=2,那么-3a=2________,
依据是等式的性质____,在等式的两边都____________________;
乘同一个数,结果仍相等
×(-3)
2
例2 根据等式性质填空
(2)如果a=2,那么 ,
依据是等式的性质____,在等式的两边都____________________
________________.
2
除以同一个不为0的数,
结果仍相等
等式的性质1:
如果a=b,那么a±c=b±c.
等式的性质2:
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
等式两边加(或减)同一个数(或式子),结果仍相等.
注意:
1. 等式两边都要参加运算,并且是作同一种运算.
2. 等式两边都不能除以0,即0不能作除数或分母.
例3. 用适当的数或式子填空,并说明是根据等式的哪一条性质以及怎样变形.
(1)因为
等式性质1
4
等式性质2
3
3
例3. 用适当的数或式子填空,并说明是根据等式的哪一条性质以及怎样变形.
(2)因为
2x
3
等式性质1
等式性质2
练习 已知 3a-2=7a-2 以下是某同学的变形过程,请找出变形过程中的错误并解答.
解:两边加2,得 3a-2+2=7a-2+2.
化简,得 3a=7a.
两边除以a,得 3=7.
反思:
等式两边都要参加运算,并且是同一种运算
等式两边都不能除以0,即0不能做除数或分母
例4 . 利用等式的性质解下列方程
(1)x+7=26
解:(1)两边减7,得
x = 19
于是
x+7-7=26-7
(2)-5x=20 (3)
解:(2)两边除以-5,得
于是
x = -4
(3)两边加5,得
化简,得
两边乘-3,得
x = -27
解以x为未知数的方程,就是把方程逐步转化为x=a(常数)的形式,等式的性质是转化的重要依据.
一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等. 例如,
将x = -27代入方程 的左边,得
方程的左右两边相等,所以x = -27是方程 的解.
A
2. 下列各式变形正确的是 ( )
A. 由3x-1= 2x+1得3x-2x =1+1
B. 由5+1= 6得5= 6+1
C. 由2(x+1) = 2y+1得x +1= y +1
D. 由2a + 3b = c-6 得2a = c-18b
1. 下列说法正确的是_______
A. 等式都是方程
B. 方程都是等式
C. 不是方程的就不是等式
D. 未知数的值就是方程的解
B
巩固练习
3. 下列变形,正确的是 ( )
A. 若ac = bc,则a = b
B. 若 ,则a = b
C. 若a2 = b2,则a = b
D. 若 ,则x = -2
B
4.用等式的性质解下列方程并检验:
(1)x-5=6; (2)0.3x=45;(3)5x+4=0.
解: (1)两边加5,得 x-5+5=6+5.
于是 x=11.
检验: 当x=11时,左边=11-5=6=右边,
所以x=11是原方程的解.
(2)两边除以0.3,得 .
于是 x=150.
检验:当x=150时,左边=0.3×150=45=右边,
所以x=150是原方程的解.
(3)两边减4,得 5x+4-4=0-4.
化简,得 5x=-4.
两边除以5,得 x= .
检验:当x= 时,左边=0=右边,
所以x= 是原方程的解.
课堂小结
等式性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
如果a=b,那么a±c=b±c.
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,
结果仍相等.
课下作业
必做:课本83页习题3.1第4题;
选做:智慧学习103页学习巩固。
