苏教版三年级下册数学第六单元 长方形和正方形的面积 单元练习 (pdf版 含答案)
文档属性
| 名称 | 苏教版三年级下册数学第六单元 长方形和正方形的面积 单元练习 (pdf版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 211.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 10:12:16 | ||
图片预览

文档简介
第六单元专项提优
专项一:巧求图形面积
例 1:如图,两张边长为 10 厘米的正方形纸,一部分重叠在一起放在桌上。桌
子被盖住的面积是多少?(单位:厘米)
分析:明确图形之间的包含关系是解决此类问题的关键。
观察图形可知,桌子被盖住的面积等于两个边长为 10 厘米的正方形的面积减去
中间重叠的一个边长为 5厘米的小正方形的面积。
解答:10×10×2=200(平方厘米) 200-5×5=175(平方厘米)
反馈练习
1.求阴影部分的面积。(单位:厘米)
2.如图,一个长方形和一个正方形部分重叠,两块没有重叠的阴影部分面积相差
多少平方厘米?
3.如图,两个完全一样的正方形部分重叠后,成为一个长方形,重叠部分长 6
厘米。已知长方形的长是 16 厘米,则长方形的面积是多少平方厘米?
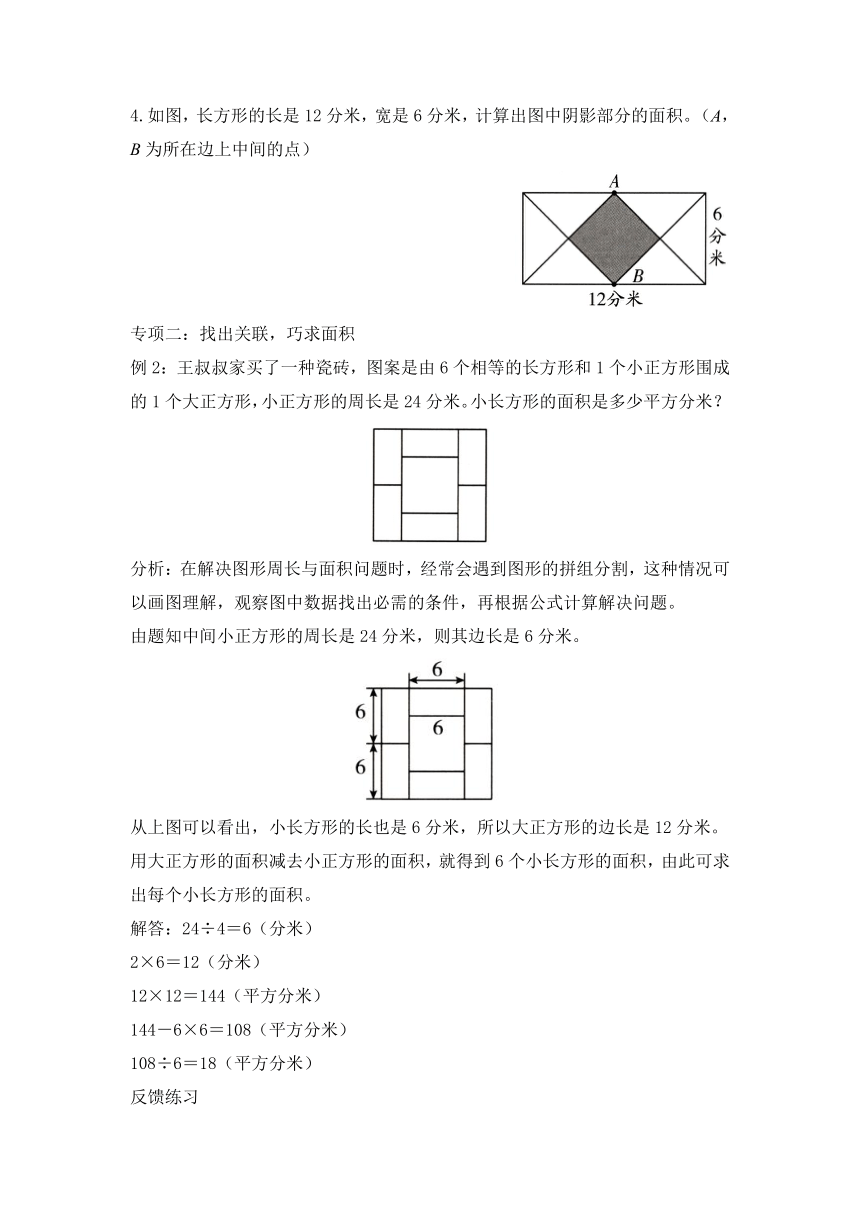
4.如图,长方形的长是 12 分米,宽是 6分米,计算出图中阴影部分的面积。(A,
B 为所在边上中间的点)
专项二:找出关联,巧求面积
例 2:王叔叔家买了一种瓷砖,图案是由 6个相等的长方形和 1个小正方形围成
的 1个大正方形,小正方形的周长是 24 分米。小长方形的面积是多少平方分米?
分析:在解决图形周长与面积问题时,经常会遇到图形的拼组分割,这种情况可
以画图理解,观察图中数据找出必需的条件,再根据公式计算解决问题。
由题知中间小正方形的周长是 24 分米,则其边长是 6分米。
从上图可以看出,小长方形的长也是 6分米,所以大正方形的边长是 12 分米。
用大正方形的面积减去小正方形的面积,就得到 6个小长方形的面积,由此可求
出每个小长方形的面积。
解答:24÷4=6(分米)
2×6=12(分米)
12×12=144(平方分米)
144-6×6=108(平方分米)
108÷6=18(平方分米)
反馈练习
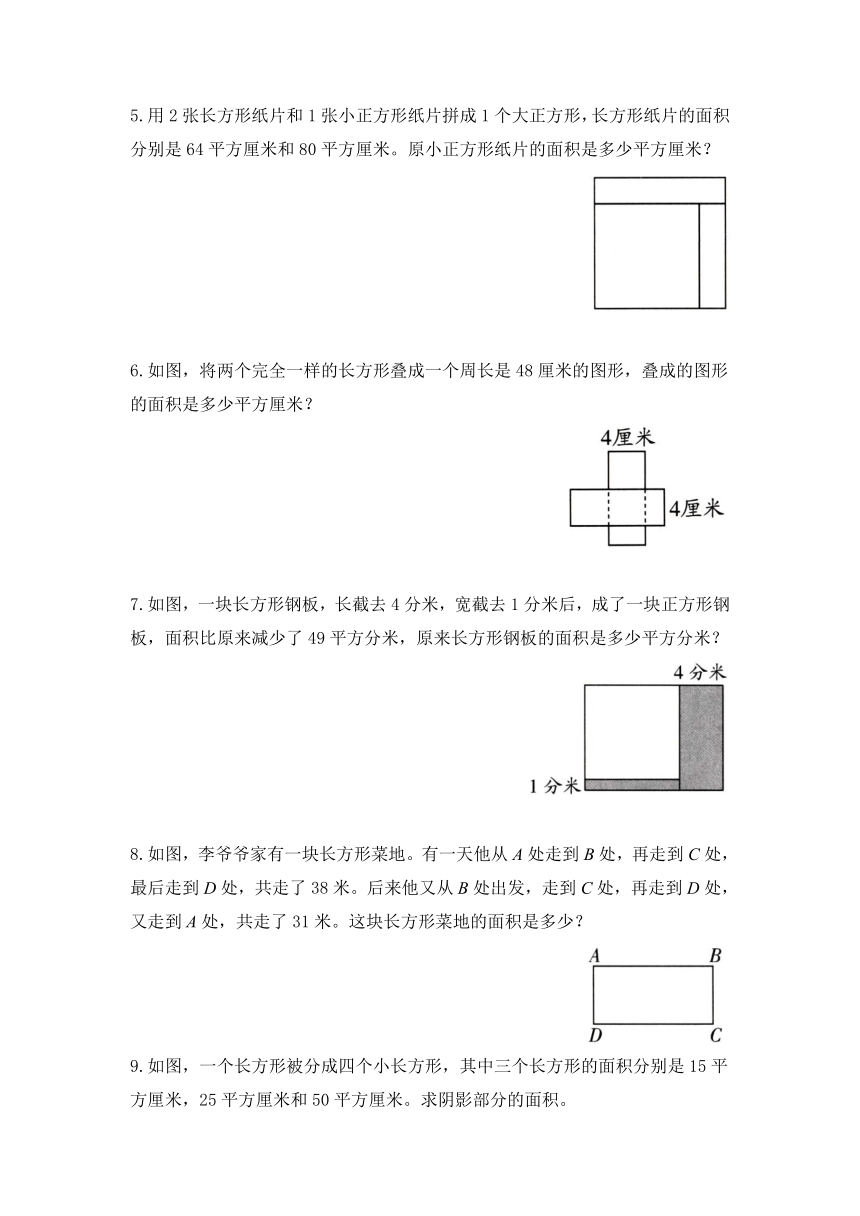
5.用 2 张长方形纸片和 1张小正方形纸片拼成 1个大正方形,长方形纸片的面积
分别是 64 平方厘米和 80 平方厘米。原小正方形纸片的面积是多少平方厘米?
6.如图,将两个完全一样的长方形叠成一个周长是 48 厘米的图形,叠成的图形
的面积是多少平方厘米?
7.如图,一块长方形钢板,长截去 4分米,宽截去 1分米后,成了一块正方形钢
板,面积比原来减少了 49 平方分米,原来长方形钢板的面积是多少平方分米?
8.如图,李爷爷家有一块长方形菜地。有一天他从 A 处走到 B 处,再走到 C 处,
最后走到 D 处,共走了 38 米。后来他又从 B 处出发,走到 C 处,再走到 D 处,
又走到 A 处,共走了 31 米。这块长方形菜地的面积是多少?
9.如图,一个长方形被分成四个小长方形,其中三个长方形的面积分别是 15 平
方厘米,25 平方厘米和 50 平方厘米。求阴影部分的面积。
参考答案
1.4×4=16(平方厘米) 6×4=24(平方厘米)
2×2=4(平方厘米) 16+24-4×2=32(平方厘米)
2.12×7=84(平方厘米) 5×5=25(平方厘米) 84-25=59(平方厘米)
提示:左边阴影部分的面积等于长方形面积减去重叠部分的面积,右边阴影部分
的面积等于正方形面积减去重叠部分的面积,因为重叠部分的面积相等,因此,
阴影部分的面积差就是原长方形和正方形的面积差。
3.(16+6)÷2=11(厘米) 16×11=176(平方厘米)
提示:长方形的长加上重叠部分的 6厘米就是原来正方形的两个边长的和,正方
形的边长等于长方形的宽。
4.6×6÷4×2=18(平方分米) 提示:因为 A,B 是长边上中间的点,而且
长是宽的 2倍。所以如果阴影部分从中间分开,相当于是边长为 6分米的正方形
的四分之一,所以 6×6÷4=9(平方分米),阴影部分的面积为 9×2=18(平
方分米)。
5.80-64=16(平方厘米) 16=4×4 64÷4=16(厘米)
16×16=256(平方厘米)
提示:如图,用大长方形的面积减去小长方形的面积,就是右上角小正方形的面
积,由此可算出小正方形的边长,也就是两个长方形的宽,就可以求出小长方形
的长,即原小正方形纸片的边长。
6.48÷4=12(厘米) 12×4×2=96(平方厘米)
96-4×4=80(平方厘米) 提示:从题图中可以看出,该图形的周长相当于
长方形 4条长边的和,因此可以先求出长方形的长,再求叠成的图形面积。
7.49-1×4=45(平方分米) 45÷(1+4)=9(分米)
9×9+49=130(平方分米)
提示:如图,将左下角阴影部分拼接到右边阴影图形上,组成 2个分别是长是 4
分米、宽是 1分米和长是正方形边长、宽是 5分米的长方形。
8.(38+31)÷3=23(米) 长:38-23=15(米) 宽:31-23=8(米)
面积:15×8=120(平方米)
提示:第一次走了 2条长和 1条宽,第二次走了 2条宽和 1条长,一共 3条长和
3条宽,可以先求出 1条长和 1条宽的和,再分别求出长和宽,从而求出面积。
9.15×2=30(平方厘米)
提示:如图,③3号长方形的面积是②号长方形面积的 2倍,它们的长相同,可
得③号长方形的宽是②号长方形宽的 2倍,那么④号长方形的宽也是①号长方形
宽的 2倍,可知④号长方形的面积也是①号长方形面积的 2倍。
专项一:巧求图形面积
例 1:如图,两张边长为 10 厘米的正方形纸,一部分重叠在一起放在桌上。桌
子被盖住的面积是多少?(单位:厘米)
分析:明确图形之间的包含关系是解决此类问题的关键。
观察图形可知,桌子被盖住的面积等于两个边长为 10 厘米的正方形的面积减去
中间重叠的一个边长为 5厘米的小正方形的面积。
解答:10×10×2=200(平方厘米) 200-5×5=175(平方厘米)
反馈练习
1.求阴影部分的面积。(单位:厘米)
2.如图,一个长方形和一个正方形部分重叠,两块没有重叠的阴影部分面积相差
多少平方厘米?
3.如图,两个完全一样的正方形部分重叠后,成为一个长方形,重叠部分长 6
厘米。已知长方形的长是 16 厘米,则长方形的面积是多少平方厘米?
4.如图,长方形的长是 12 分米,宽是 6分米,计算出图中阴影部分的面积。(A,
B 为所在边上中间的点)
专项二:找出关联,巧求面积
例 2:王叔叔家买了一种瓷砖,图案是由 6个相等的长方形和 1个小正方形围成
的 1个大正方形,小正方形的周长是 24 分米。小长方形的面积是多少平方分米?
分析:在解决图形周长与面积问题时,经常会遇到图形的拼组分割,这种情况可
以画图理解,观察图中数据找出必需的条件,再根据公式计算解决问题。
由题知中间小正方形的周长是 24 分米,则其边长是 6分米。
从上图可以看出,小长方形的长也是 6分米,所以大正方形的边长是 12 分米。
用大正方形的面积减去小正方形的面积,就得到 6个小长方形的面积,由此可求
出每个小长方形的面积。
解答:24÷4=6(分米)
2×6=12(分米)
12×12=144(平方分米)
144-6×6=108(平方分米)
108÷6=18(平方分米)
反馈练习
5.用 2 张长方形纸片和 1张小正方形纸片拼成 1个大正方形,长方形纸片的面积
分别是 64 平方厘米和 80 平方厘米。原小正方形纸片的面积是多少平方厘米?
6.如图,将两个完全一样的长方形叠成一个周长是 48 厘米的图形,叠成的图形
的面积是多少平方厘米?
7.如图,一块长方形钢板,长截去 4分米,宽截去 1分米后,成了一块正方形钢
板,面积比原来减少了 49 平方分米,原来长方形钢板的面积是多少平方分米?
8.如图,李爷爷家有一块长方形菜地。有一天他从 A 处走到 B 处,再走到 C 处,
最后走到 D 处,共走了 38 米。后来他又从 B 处出发,走到 C 处,再走到 D 处,
又走到 A 处,共走了 31 米。这块长方形菜地的面积是多少?
9.如图,一个长方形被分成四个小长方形,其中三个长方形的面积分别是 15 平
方厘米,25 平方厘米和 50 平方厘米。求阴影部分的面积。
参考答案
1.4×4=16(平方厘米) 6×4=24(平方厘米)
2×2=4(平方厘米) 16+24-4×2=32(平方厘米)
2.12×7=84(平方厘米) 5×5=25(平方厘米) 84-25=59(平方厘米)
提示:左边阴影部分的面积等于长方形面积减去重叠部分的面积,右边阴影部分
的面积等于正方形面积减去重叠部分的面积,因为重叠部分的面积相等,因此,
阴影部分的面积差就是原长方形和正方形的面积差。
3.(16+6)÷2=11(厘米) 16×11=176(平方厘米)
提示:长方形的长加上重叠部分的 6厘米就是原来正方形的两个边长的和,正方
形的边长等于长方形的宽。
4.6×6÷4×2=18(平方分米) 提示:因为 A,B 是长边上中间的点,而且
长是宽的 2倍。所以如果阴影部分从中间分开,相当于是边长为 6分米的正方形
的四分之一,所以 6×6÷4=9(平方分米),阴影部分的面积为 9×2=18(平
方分米)。
5.80-64=16(平方厘米) 16=4×4 64÷4=16(厘米)
16×16=256(平方厘米)
提示:如图,用大长方形的面积减去小长方形的面积,就是右上角小正方形的面
积,由此可算出小正方形的边长,也就是两个长方形的宽,就可以求出小长方形
的长,即原小正方形纸片的边长。
6.48÷4=12(厘米) 12×4×2=96(平方厘米)
96-4×4=80(平方厘米) 提示:从题图中可以看出,该图形的周长相当于
长方形 4条长边的和,因此可以先求出长方形的长,再求叠成的图形面积。
7.49-1×4=45(平方分米) 45÷(1+4)=9(分米)
9×9+49=130(平方分米)
提示:如图,将左下角阴影部分拼接到右边阴影图形上,组成 2个分别是长是 4
分米、宽是 1分米和长是正方形边长、宽是 5分米的长方形。
8.(38+31)÷3=23(米) 长:38-23=15(米) 宽:31-23=8(米)
面积:15×8=120(平方米)
提示:第一次走了 2条长和 1条宽,第二次走了 2条宽和 1条长,一共 3条长和
3条宽,可以先求出 1条长和 1条宽的和,再分别求出长和宽,从而求出面积。
9.15×2=30(平方厘米)
提示:如图,③3号长方形的面积是②号长方形面积的 2倍,它们的长相同,可
得③号长方形的宽是②号长方形宽的 2倍,那么④号长方形的宽也是①号长方形
宽的 2倍,可知④号长方形的面积也是①号长方形面积的 2倍。
