新人教版高中物理必修二 第五章 第二节 运动的合成与分解 (共20张PPT)
文档属性
| 名称 | 新人教版高中物理必修二 第五章 第二节 运动的合成与分解 (共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-15 13:02:46 | ||
图片预览








文档简介
(共20张PPT)
运动的合成与分解
5.2
问题
若人在河中始终保持头朝正前方游向对岸,你认为他会在对岸的正前方到达,还是会偏向上游或下游?为什么?
对类似上述的运动应该怎样分析呢?
下面让我们从一个简单的平面运动开始研究。
一个平面运动的实例
观察蜡块的运动
在一端封闭、长约 1 m 的玻璃管内注满清水,水中放一个红蜡做的小圆柱体 A,将玻璃管的开口端用橡胶塞塞紧。把玻璃管倒置,蜡块 A 沿玻璃管上升。
一个平面运动的实例
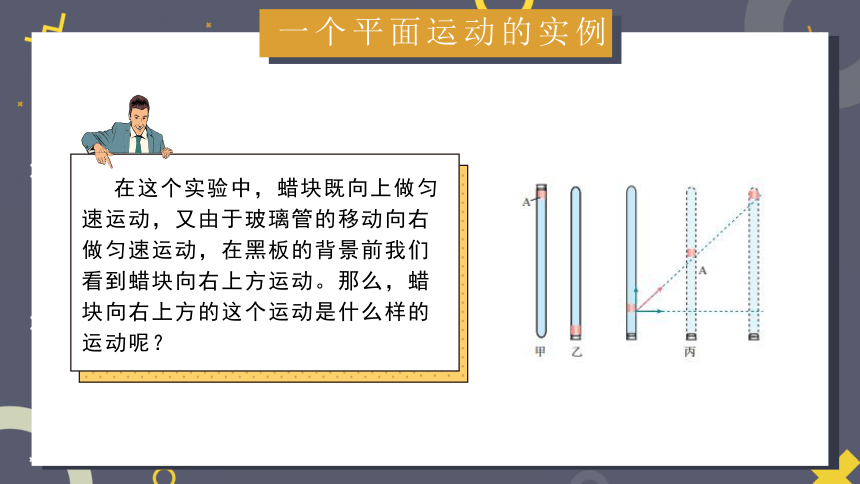
在这个实验中,蜡块既向上做匀速运动,又由于玻璃管的移动向右做匀速运动,在黑板的背景前我们看到蜡块向右上方运动。那么,蜡块向右上方的这个运动是什么样的运动呢?
建立坐标系
一个平面运动的实例
要想定量地研究蜡块的运动,就要建立坐标系,具体分析
研究物体的运动时,坐标系的选取很重要。例如,对于直线运动,最好沿着这条直线建立坐标系。但是,有时在对运动作深入分析之前,物体的运动形式并不清楚,甚至难以判断它的运动轨迹是不是直线。这时,就需要选择其他类型的坐标系。研究物体在平面内的运动时,可以选择平面直角坐标系。
建立坐标系
一个平面运动的实例
要想定量地研究蜡块的运动,就要建立坐标系,具体分析
在研究蜡块的运动时,我们以蜡块开始匀速运动的位置为原点 O,以水平向右的方向和竖直向上的方向分别为 x轴和 y 轴的方向,建立平面直角坐标系(图5.2-2)。
一个平面运动的实例
要确定蜡块运动的轨迹,首先要确定任意时刻蜡块的位置。我们设法写出蜡块的坐标随时间变化的关系式。蜡块 x 坐标的值等于它与 y 轴的距离,y 坐标的值等于它与 x轴的距离。
若以vx 表示玻璃管向右移动的速度,以 vy 表示蜡块沿玻璃管上升的速度,则有
一个平面运动的实例
蜡块沿着什么样的轨迹运动?在数学上,关于 x、y 两个变量的关系式可以描述一条曲线(包括直线),而在上面 x、y 的表达式中,除了x、y 之外还有一个变量 t,我们可以从中消去 t,这样就得到
一个平面运动的实例
蜡块沿着什么样的轨迹运动?在数学上,关于 x、y 两个变量的关系式可以描述一条曲线(包括直线),而在上面 x、y 的表达式中,除了x、y 之外还有一个变量 t,我们可以从中消去 t,这样就得到
由 于vx 和vy都 是 常 量,可见右侧公式代表的是一条过原点的直线,也就是说,蜡块的运动轨迹是直线。
一个平面运动的实例
速度 v 与vx、vy 的关系已经在图5.2-2 中形象地标出,因此可以根据勾股定理写出它们之间的关系
根据三角函数的知识,从图5.2-2 中还可以确定速度v的方向,即用速度矢量v与x轴正方向的夹角θ来表示,它的正切为
运动的合成与分解
在这个实例中,我们看到蜡块向右上方的运动可以看成由沿玻璃管向上的运动和水平向右的运动共同构成。
蜡块沿玻璃管向上的运动和它随着玻璃管向右的运动,都叫作分运动;而蜡块相对于黑板向右上方的运动叫作合运动。
由分运动求合运动的过程,叫作运动的合成
由合运动求分运动的过程,叫作运动的分解
运动的合成与分解遵从矢量运算法则
运动的合成与分解
某商场设有步行楼梯和自动扶梯,步行楼梯每级的高度是 0.15 m,自动扶梯与水平面的夹角为 30°,自动扶梯前进的速度是 0.76 m/s。有甲、乙两位顾客,分别从自动扶梯和步行楼梯的起点同时上楼,甲在自动扶梯上站立不动,乙在步行楼梯上以每秒上两个台阶的速度匀速上楼(图5.2-3)。哪位顾客先到达楼上?如果该楼层高4.56 m,甲上楼用了多少时间?
运动的合成与分解
如图 5.2-4 所示,甲在竖直方向的速度
乙在竖直方向的速度
因此 v 甲y > v 乙 ,甲先到楼上。
甲比乙先到达楼上,甲上楼用了 12 s。
运动的合成与分解
运动的合成与分解是分析复杂运动时常用的方法。虽然本节实验中的两个分运动都是匀速运动,但运动合成与分解的思想和方法对分运动是变速运动的情况也是适用的。
运动的合成与分解
在图 5.2-1 所示的实验中,如果将玻璃管紧贴着黑板沿水平方向向右匀加速移动,若玻璃管内壁是光滑的,蜡块的轨迹还是一条直线吗?
练习与应用
炮筒与水平方向成 30°角(图 5.2-5),炮弹从炮口射出时的速度大小是 800 m/s,这个速度在水平方向和竖直方向的分速度各是多大?
练习与应用
2.在许多情况下,跳伞员跳伞后最初一段时间降落伞并不张开,跳伞员做加速运动。随后,降落伞张开,跳伞员做减速运动。速度减小到一定值后便不再减小,跳伞员以这一速度做匀速运动,直至落地。无风时某跳伞员竖直下落,着地时速度是5m/s。现在有风,运动员在竖直方向的运动情况与无风时相同,并且风使他以4m/s的速度沿水平方向运动。跳伞员将以多大速度着地画出速度合成的图示。
练习与应用
3.一艘炮舰沿河由西向东行驶,在炮舰上发炮射击北岸的目标。要击中目标,射击方向应直接对准目标,还是应该偏东或偏西一些作俯视图,并说明理由。
练习与应用
4.在图的实验中,假设从某时刻(t=0)开始,红蜡块在玻璃管内每1s上升的距离都是10cm,与此同时,玻璃管向右沿水平方向匀加速平移,每1s内的位移依次是4cm、12cm、20cm、28cm。在图所示的坐标系中,y表示蜡块在竖直方向的位移,x表示蜡块随玻璃管通过的水平位移,t=0时蜡块位于坐标原点。请在图中标出t等于1s、2s、3s、4s时蜡块的位置,并用平滑曲线描绘蜡块的轨迹。
练习与应用
5.汽艇以18km/h的速度沿垂直于河岸的方向匀速向对岸行驶,河宽500m。设想河水不流动,汽艇驶到对岸需要多长时间如果河水流速是h,汽艇驶到对岸需要多长时间汽艇在对岸何处靠岸
运动的合成与分解
5.2
问题
若人在河中始终保持头朝正前方游向对岸,你认为他会在对岸的正前方到达,还是会偏向上游或下游?为什么?
对类似上述的运动应该怎样分析呢?
下面让我们从一个简单的平面运动开始研究。
一个平面运动的实例
观察蜡块的运动
在一端封闭、长约 1 m 的玻璃管内注满清水,水中放一个红蜡做的小圆柱体 A,将玻璃管的开口端用橡胶塞塞紧。把玻璃管倒置,蜡块 A 沿玻璃管上升。
一个平面运动的实例
在这个实验中,蜡块既向上做匀速运动,又由于玻璃管的移动向右做匀速运动,在黑板的背景前我们看到蜡块向右上方运动。那么,蜡块向右上方的这个运动是什么样的运动呢?
建立坐标系
一个平面运动的实例
要想定量地研究蜡块的运动,就要建立坐标系,具体分析
研究物体的运动时,坐标系的选取很重要。例如,对于直线运动,最好沿着这条直线建立坐标系。但是,有时在对运动作深入分析之前,物体的运动形式并不清楚,甚至难以判断它的运动轨迹是不是直线。这时,就需要选择其他类型的坐标系。研究物体在平面内的运动时,可以选择平面直角坐标系。
建立坐标系
一个平面运动的实例
要想定量地研究蜡块的运动,就要建立坐标系,具体分析
在研究蜡块的运动时,我们以蜡块开始匀速运动的位置为原点 O,以水平向右的方向和竖直向上的方向分别为 x轴和 y 轴的方向,建立平面直角坐标系(图5.2-2)。
一个平面运动的实例
要确定蜡块运动的轨迹,首先要确定任意时刻蜡块的位置。我们设法写出蜡块的坐标随时间变化的关系式。蜡块 x 坐标的值等于它与 y 轴的距离,y 坐标的值等于它与 x轴的距离。
若以vx 表示玻璃管向右移动的速度,以 vy 表示蜡块沿玻璃管上升的速度,则有
一个平面运动的实例
蜡块沿着什么样的轨迹运动?在数学上,关于 x、y 两个变量的关系式可以描述一条曲线(包括直线),而在上面 x、y 的表达式中,除了x、y 之外还有一个变量 t,我们可以从中消去 t,这样就得到
一个平面运动的实例
蜡块沿着什么样的轨迹运动?在数学上,关于 x、y 两个变量的关系式可以描述一条曲线(包括直线),而在上面 x、y 的表达式中,除了x、y 之外还有一个变量 t,我们可以从中消去 t,这样就得到
由 于vx 和vy都 是 常 量,可见右侧公式代表的是一条过原点的直线,也就是说,蜡块的运动轨迹是直线。
一个平面运动的实例
速度 v 与vx、vy 的关系已经在图5.2-2 中形象地标出,因此可以根据勾股定理写出它们之间的关系
根据三角函数的知识,从图5.2-2 中还可以确定速度v的方向,即用速度矢量v与x轴正方向的夹角θ来表示,它的正切为
运动的合成与分解
在这个实例中,我们看到蜡块向右上方的运动可以看成由沿玻璃管向上的运动和水平向右的运动共同构成。
蜡块沿玻璃管向上的运动和它随着玻璃管向右的运动,都叫作分运动;而蜡块相对于黑板向右上方的运动叫作合运动。
由分运动求合运动的过程,叫作运动的合成
由合运动求分运动的过程,叫作运动的分解
运动的合成与分解遵从矢量运算法则
运动的合成与分解
某商场设有步行楼梯和自动扶梯,步行楼梯每级的高度是 0.15 m,自动扶梯与水平面的夹角为 30°,自动扶梯前进的速度是 0.76 m/s。有甲、乙两位顾客,分别从自动扶梯和步行楼梯的起点同时上楼,甲在自动扶梯上站立不动,乙在步行楼梯上以每秒上两个台阶的速度匀速上楼(图5.2-3)。哪位顾客先到达楼上?如果该楼层高4.56 m,甲上楼用了多少时间?
运动的合成与分解
如图 5.2-4 所示,甲在竖直方向的速度
乙在竖直方向的速度
因此 v 甲y > v 乙 ,甲先到楼上。
甲比乙先到达楼上,甲上楼用了 12 s。
运动的合成与分解
运动的合成与分解是分析复杂运动时常用的方法。虽然本节实验中的两个分运动都是匀速运动,但运动合成与分解的思想和方法对分运动是变速运动的情况也是适用的。
运动的合成与分解
在图 5.2-1 所示的实验中,如果将玻璃管紧贴着黑板沿水平方向向右匀加速移动,若玻璃管内壁是光滑的,蜡块的轨迹还是一条直线吗?
练习与应用
炮筒与水平方向成 30°角(图 5.2-5),炮弹从炮口射出时的速度大小是 800 m/s,这个速度在水平方向和竖直方向的分速度各是多大?
练习与应用
2.在许多情况下,跳伞员跳伞后最初一段时间降落伞并不张开,跳伞员做加速运动。随后,降落伞张开,跳伞员做减速运动。速度减小到一定值后便不再减小,跳伞员以这一速度做匀速运动,直至落地。无风时某跳伞员竖直下落,着地时速度是5m/s。现在有风,运动员在竖直方向的运动情况与无风时相同,并且风使他以4m/s的速度沿水平方向运动。跳伞员将以多大速度着地画出速度合成的图示。
练习与应用
3.一艘炮舰沿河由西向东行驶,在炮舰上发炮射击北岸的目标。要击中目标,射击方向应直接对准目标,还是应该偏东或偏西一些作俯视图,并说明理由。
练习与应用
4.在图的实验中,假设从某时刻(t=0)开始,红蜡块在玻璃管内每1s上升的距离都是10cm,与此同时,玻璃管向右沿水平方向匀加速平移,每1s内的位移依次是4cm、12cm、20cm、28cm。在图所示的坐标系中,y表示蜡块在竖直方向的位移,x表示蜡块随玻璃管通过的水平位移,t=0时蜡块位于坐标原点。请在图中标出t等于1s、2s、3s、4s时蜡块的位置,并用平滑曲线描绘蜡块的轨迹。
练习与应用
5.汽艇以18km/h的速度沿垂直于河岸的方向匀速向对岸行驶,河宽500m。设想河水不流动,汽艇驶到对岸需要多长时间如果河水流速是h,汽艇驶到对岸需要多长时间汽艇在对岸何处靠岸
