数学人教A版(2019)必修第一册4.3.2对数的运算 课件(共22张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.3.2对数的运算 课件(共22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 14:22:34 | ||
图片预览








文档简介
(共22张PPT)
数 学 人 教 版 必 修 第 一 册
第四章 指数函数与对数函数
4.3.2 对数的运算
2022年11月15日星期二11时57分12秒
2022年11月15日星期二11时57分12秒
4.3.2 对数的运算
对数的创始人是苏格兰数学家纳皮尔(Napier,1550年~1617年)。他发明了供天文计算作参考的对数,并于1614年在爱丁堡出版了《奇妙的对数定律说明书》,公布了他的发明。恩格斯把对数的发明与解析几何的创始,微积分的建立并称为17世纪数学的三大成就。
课程标准:掌握积、商、幂的对数运算性质,理解
其推导过程和成立的条件.
教学难点:灵活运用对数运算性质
教学重点:对数的运算性质
1.对数的定义
如果a(a>0且a≠1)的b次幂等于N,就是______,那么数b叫做_______________,记作________,其中a叫做对数的________,N叫做________.
ab=N
以a为底N的对数
b=logaN
底数
真数
复习引入
2.两种特殊的对数
(1)通常将以10为底的对数叫________,log10N简记为________.
(2)通常以e为底,(e为无理数,e≈__________)的对数叫 ______,logeN简记为________.
常用对数
lg N
2.718 28…
自然对数
ln N
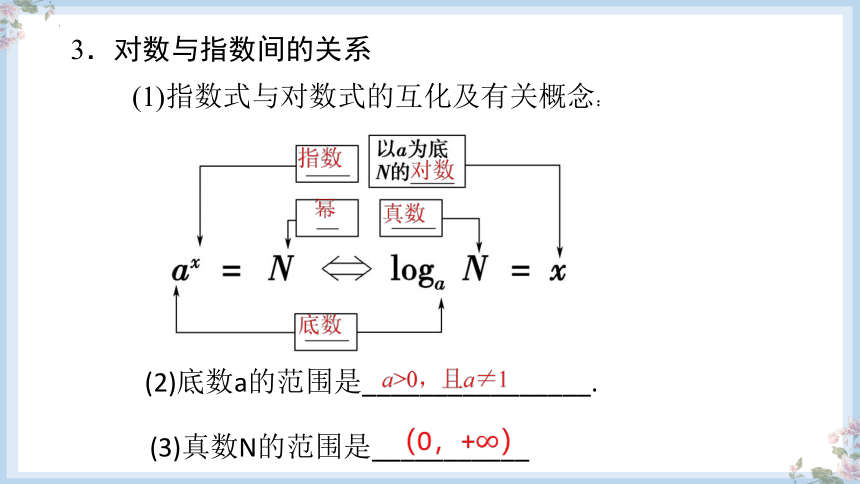
3.对数与指数间的关系
(1)指数式与对数式的互化及有关概念:
(2)底数a的范围是________________.
(3)真数N的范围是___________
(0,+)
新知探索
在引入对数之后,自然应研究对数的运算性质.你认为可以怎样研究?
我们知道了对数与指数间的关系,能否利用指数幂运算性质得出相应的对数运算性质呢?
第一步:我们不妨将转化为
第二步:令= ,=, 易得
第三步:替换后,就得到了对数的一个运算性质
动手
试一试:
你能否仿照上述过程,由 推出对数运算的其它性质呢
第一步:我们不妨将转化为
第二步:令= ,=, 易得
第三步:替换后,又得到了对数的一个运算性质
第一步:我们不妨将转化为
第二步:令=, 易得
第三步:替换后,又得到了对数的一个运算性质
你能否仿照上述过程,由 推出对数运算的其它性质呢
于是,我们得到如下的对数运算性质:
新知整理
对数的运算性质把乘积转化为加法,把商转化为减法,把乘方转化为乘法,降低了运算级别,简化了运算。
【课堂小练】
( )
1.判断题
(1)积、商的对数可以化为对数的和、差.( ) (2)loga(xy)=loga x·loga y ( )
(3)loga(x+y)=loga x·loga y ( )
(4)log2(-7)2=2log2(-7) ( )
【课堂小练】
(1)计算log84+log82等于( )A.log86 B.8 C.6 D.1
(2)计算log510-log52等于( )
A.log58 B.lg 5 C.1 D. 2
2.选择题
3.填空题(请把正确的答案写在横线上) (1)log325-log35=________. (2)lg 8+lg =________. (3)log48=________.
3
log35
【课堂小练】
【例题讲解】
例1 求下列各式的值:
解:
【例题讲解】
例2 用 表示 :
解:
(1)4lg 2+3lg 5-lg
【跟踪训练】
1 计算下列各式的值:
解:原式=lg =lg 104=4
(2)lg 52+lg 8+lg 5·lg 20+(lg 2)2
(2)lg 52+lg 8+lg 5·lg 20+(lg 2)2
【跟踪训练】
解:原式=2lg 5+2lg 2+lg 5×(1+lg 2)+(lg 2)2
=2(lg 5+lg 2)+lg 5+lg 2(lg 5+lg 2)
=2+lg 5+lg 2
=2+1=3.
1.利用对数性质求值的解题关键是化异为同,先使各项底数相同,再找真数间的联系.
2.对于复杂的运算式,可先化简再计算;化简问题的常用方法: ①“拆”:将积(商)的对数拆成两对数之和(差); ②“收”:将同底对数的和(差)收成积(商)的对数.
【方法总结】
【新知拓展】
(1)推广:loga(N1N2…Nk)=logaN1+logaN2+…+logaNk(Nk>0,k∈N*).
(2)只有当式子中所有的对数都有意义时,对数的运算性质才能成立,注意下列式子不成立:
loga(MN)=logaM·logaN,
loga(M±N)=logaM±logaN,
loga=,
【教学小结】
爱学习的孩子才是好孩子
对数运算性质推导的基本方法:利用对数的定义将对数问题转化为指数问题,再利用幂的运算性质,进行转化变形,然后把它还原为对数问题.
第一步:我们不妨将
转化为
第二步:令 ,, 易得
第三步:替换得到了对数的一个
运算性质
【教学小结】
爱学习的孩子才是好孩子
对数运算性质的实质就是把积、商、幂的对数运算分别转化为对数的加、减、乘运算,使用时要注意公式的适用条件.
谢谢大家
2022年11月15日星期二11时57分12秒
数 学 人 教 版 必 修 第 一 册
第四章 指数函数与对数函数
4.3.2 对数的运算
2022年11月15日星期二11时57分12秒
2022年11月15日星期二11时57分12秒
4.3.2 对数的运算
对数的创始人是苏格兰数学家纳皮尔(Napier,1550年~1617年)。他发明了供天文计算作参考的对数,并于1614年在爱丁堡出版了《奇妙的对数定律说明书》,公布了他的发明。恩格斯把对数的发明与解析几何的创始,微积分的建立并称为17世纪数学的三大成就。
课程标准:掌握积、商、幂的对数运算性质,理解
其推导过程和成立的条件.
教学难点:灵活运用对数运算性质
教学重点:对数的运算性质
1.对数的定义
如果a(a>0且a≠1)的b次幂等于N,就是______,那么数b叫做_______________,记作________,其中a叫做对数的________,N叫做________.
ab=N
以a为底N的对数
b=logaN
底数
真数
复习引入
2.两种特殊的对数
(1)通常将以10为底的对数叫________,log10N简记为________.
(2)通常以e为底,(e为无理数,e≈__________)的对数叫 ______,logeN简记为________.
常用对数
lg N
2.718 28…
自然对数
ln N
3.对数与指数间的关系
(1)指数式与对数式的互化及有关概念:
(2)底数a的范围是________________.
(3)真数N的范围是___________
(0,+)
新知探索
在引入对数之后,自然应研究对数的运算性质.你认为可以怎样研究?
我们知道了对数与指数间的关系,能否利用指数幂运算性质得出相应的对数运算性质呢?
第一步:我们不妨将转化为
第二步:令= ,=, 易得
第三步:替换后,就得到了对数的一个运算性质
动手
试一试:
你能否仿照上述过程,由 推出对数运算的其它性质呢
第一步:我们不妨将转化为
第二步:令= ,=, 易得
第三步:替换后,又得到了对数的一个运算性质
第一步:我们不妨将转化为
第二步:令=, 易得
第三步:替换后,又得到了对数的一个运算性质
你能否仿照上述过程,由 推出对数运算的其它性质呢
于是,我们得到如下的对数运算性质:
新知整理
对数的运算性质把乘积转化为加法,把商转化为减法,把乘方转化为乘法,降低了运算级别,简化了运算。
【课堂小练】
( )
1.判断题
(1)积、商的对数可以化为对数的和、差.( ) (2)loga(xy)=loga x·loga y ( )
(3)loga(x+y)=loga x·loga y ( )
(4)log2(-7)2=2log2(-7) ( )
【课堂小练】
(1)计算log84+log82等于( )A.log86 B.8 C.6 D.1
(2)计算log510-log52等于( )
A.log58 B.lg 5 C.1 D. 2
2.选择题
3.填空题(请把正确的答案写在横线上) (1)log325-log35=________. (2)lg 8+lg =________. (3)log48=________.
3
log35
【课堂小练】
【例题讲解】
例1 求下列各式的值:
解:
【例题讲解】
例2 用 表示 :
解:
(1)4lg 2+3lg 5-lg
【跟踪训练】
1 计算下列各式的值:
解:原式=lg =lg 104=4
(2)lg 52+lg 8+lg 5·lg 20+(lg 2)2
(2)lg 52+lg 8+lg 5·lg 20+(lg 2)2
【跟踪训练】
解:原式=2lg 5+2lg 2+lg 5×(1+lg 2)+(lg 2)2
=2(lg 5+lg 2)+lg 5+lg 2(lg 5+lg 2)
=2+lg 5+lg 2
=2+1=3.
1.利用对数性质求值的解题关键是化异为同,先使各项底数相同,再找真数间的联系.
2.对于复杂的运算式,可先化简再计算;化简问题的常用方法: ①“拆”:将积(商)的对数拆成两对数之和(差); ②“收”:将同底对数的和(差)收成积(商)的对数.
【方法总结】
【新知拓展】
(1)推广:loga(N1N2…Nk)=logaN1+logaN2+…+logaNk(Nk>0,k∈N*).
(2)只有当式子中所有的对数都有意义时,对数的运算性质才能成立,注意下列式子不成立:
loga(MN)=logaM·logaN,
loga(M±N)=logaM±logaN,
loga=,
【教学小结】
爱学习的孩子才是好孩子
对数运算性质推导的基本方法:利用对数的定义将对数问题转化为指数问题,再利用幂的运算性质,进行转化变形,然后把它还原为对数问题.
第一步:我们不妨将
转化为
第二步:令 ,, 易得
第三步:替换得到了对数的一个
运算性质
【教学小结】
爱学习的孩子才是好孩子
对数运算性质的实质就是把积、商、幂的对数运算分别转化为对数的加、减、乘运算,使用时要注意公式的适用条件.
谢谢大家
2022年11月15日星期二11时57分12秒
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
