人教B版(2019)数学必修第一册1.2.1全称量词与存在量词 课件(共17张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册1.2.1全称量词与存在量词 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 978.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 15:34:52 | ||
图片预览






文档简介
1.2.1 全称量词与存在量词
高一
必修一
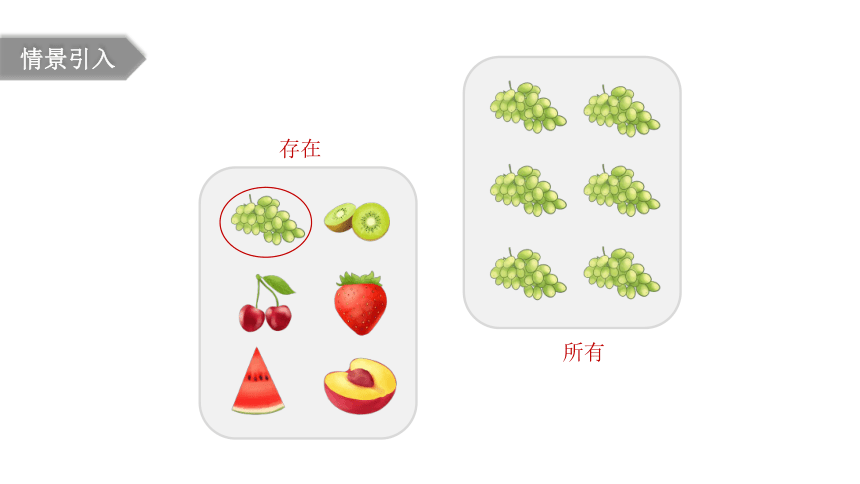
情景引入
存在
所有
本节目标
1. 理解全称量词与存在量词的意义.
2.会判定全称命题和特称命题的真假.
任务一:知识预习
课前预习
预习课本,思考并完成以下问题
1.全称量词、全称量词命题的定义是什么?
2.存在量词、存在量词命题的定义是什么?
课前预习
任务二:简单题型通关
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)在全称量词命题和存在量词命题中,量词都可以省略( )
(2)“有的等差数列也是等比数列”是存在量词命题( )
(3)“三角形内角和是180°”是全称量词命题( )
×
√
√
课前预习
任务二:简单题型通关
2.下列全称量词命题为真命题的是( )
A.所有的质数是奇数
B.?x∈R,x2+1≥1
C.对每一个无理数x,x2也是无理数
D.所有的能被5整除的整数,其末位数字都是5
B
新知精讲
1.全称量词与全称量词命题
新知精讲
2.存在量词与存在量词命题
题型探究
例1 判断下列语句是全称命题,还是特称命题.
(1)凸多边形的外角和等于360°;
(2)有的三角形内角和不是180°;
(3)对任意实数x,都有x 2+2 x+1>0;
(4)矩形的对角线不相等;
(5)若一个四边形是菱形,则这个四边形的对角线互相垂直.
题型一 全称量词命题与存在量词命题的判断
所有
全称量词命题
存在量词命题
全称量词命题
所有
全称量词命题
所有菱形
全称量词命题
归纳总结
判断一个语句是全称量词命题还是存在量词命题的思路
易错提示: 全称量词命题可能省略全称量词,存在量词命题的存在量词一般不能省略.
活学活用
(1)不等式x2+x+1>0恒成立;
(2)当x为有理数时,x2+x+1也是有理数;
(3)正数的绝对值是它本身.
(4)方程3x-2y=10有整数解.
1.用全称量词或存在量词表示下列语句
对任意实数x,不等式????????x2+????????x+1>0成立.
?
对任意有理数x,????????x2+????????x+1是有理数
?
所有正数的绝对值是它本身
存在一对整数x,y,使3x-2y=10成立.
题型探究
题型二 全称量词命题与存在量词命题的真假判断
例2 判断下列命题中的真假
1.有些实数是无限不循环小数( )
2.每一个5的倍数都是末位是0的整数 ( )
3.存在一个三角形不是等腰三角形( )
4.线段垂直平分线上的点到这条线段两个端点的距离相等( )
真
假
真
真
题型探究
题型二 全称量词命题与存在量词命题的真假判断
例3 下列命题中的假命题是( )
A.?x0∈R,x0>0
B.?x0∈R,x2+2x+1=0
C.?x∈R,x2>0
D.?x∈Z,|x|∈N
x0=1时,x0>0
真
x=-1时,x2+2x+1=0
x=0时,x2=0
x∈Z,|x|∈N恒成立
真
假
真
C
归纳总结
全称量词命题与存在量词命题的真假判断的技巧
(1)要判定一个全称量词命题是真命题,必须对限定集合M中的每个元素x验证p(x)成立;但要判定全称量词命题是假命题,只要能举出集合M中的一个x0,使得p(x0)不成立即可.
(2)要判定一个存在量词命题是真命题,只要在限定集合M中,能找到一个x0使p(x0)成立即可;否则,这个存在量词命题就是假命题.
活学活用
2.指出下列命题是全称量词命题,还是存在量词命题,并判断真假.
(1) ?x∈R ,x2-x+1=0
(2)任意两个等边三角形都相似;
(3)有些平行四边形是菱形;
(4)?x0∈R,使????02+1<0.
?
全称量词命题
假
全称量词命题
真
存在量词命题
存在量词命题
真
假
达标检测
1.下列命题中,真命题是( )
A.?x0∈R,????????0≤0
B.?x∈R,2x>x2
C.a+b=0的充要条件是????????=-1
D.a>1,b>1是ab>1的充分条件
?
D
假
?x∈R,ex>0
当x=2时,2x=x2
假
b可取0
b不可取0
假
真
本课小结
1.判断全称命题真假的步骤为“先找反例后证明”.
2.判断特称命题真假的步骤为“先找正例后证明”.
高一
必修一
情景引入
存在
所有
本节目标
1. 理解全称量词与存在量词的意义.
2.会判定全称命题和特称命题的真假.
任务一:知识预习
课前预习
预习课本,思考并完成以下问题
1.全称量词、全称量词命题的定义是什么?
2.存在量词、存在量词命题的定义是什么?
课前预习
任务二:简单题型通关
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)在全称量词命题和存在量词命题中,量词都可以省略( )
(2)“有的等差数列也是等比数列”是存在量词命题( )
(3)“三角形内角和是180°”是全称量词命题( )
×
√
√
课前预习
任务二:简单题型通关
2.下列全称量词命题为真命题的是( )
A.所有的质数是奇数
B.?x∈R,x2+1≥1
C.对每一个无理数x,x2也是无理数
D.所有的能被5整除的整数,其末位数字都是5
B
新知精讲
1.全称量词与全称量词命题
新知精讲
2.存在量词与存在量词命题
题型探究
例1 判断下列语句是全称命题,还是特称命题.
(1)凸多边形的外角和等于360°;
(2)有的三角形内角和不是180°;
(3)对任意实数x,都有x 2+2 x+1>0;
(4)矩形的对角线不相等;
(5)若一个四边形是菱形,则这个四边形的对角线互相垂直.
题型一 全称量词命题与存在量词命题的判断
所有
全称量词命题
存在量词命题
全称量词命题
所有
全称量词命题
所有菱形
全称量词命题
归纳总结
判断一个语句是全称量词命题还是存在量词命题的思路
易错提示: 全称量词命题可能省略全称量词,存在量词命题的存在量词一般不能省略.
活学活用
(1)不等式x2+x+1>0恒成立;
(2)当x为有理数时,x2+x+1也是有理数;
(3)正数的绝对值是它本身.
(4)方程3x-2y=10有整数解.
1.用全称量词或存在量词表示下列语句
对任意实数x,不等式????????x2+????????x+1>0成立.
?
对任意有理数x,????????x2+????????x+1是有理数
?
所有正数的绝对值是它本身
存在一对整数x,y,使3x-2y=10成立.
题型探究
题型二 全称量词命题与存在量词命题的真假判断
例2 判断下列命题中的真假
1.有些实数是无限不循环小数( )
2.每一个5的倍数都是末位是0的整数 ( )
3.存在一个三角形不是等腰三角形( )
4.线段垂直平分线上的点到这条线段两个端点的距离相等( )
真
假
真
真
题型探究
题型二 全称量词命题与存在量词命题的真假判断
例3 下列命题中的假命题是( )
A.?x0∈R,x0>0
B.?x0∈R,x2+2x+1=0
C.?x∈R,x2>0
D.?x∈Z,|x|∈N
x0=1时,x0>0
真
x=-1时,x2+2x+1=0
x=0时,x2=0
x∈Z,|x|∈N恒成立
真
假
真
C
归纳总结
全称量词命题与存在量词命题的真假判断的技巧
(1)要判定一个全称量词命题是真命题,必须对限定集合M中的每个元素x验证p(x)成立;但要判定全称量词命题是假命题,只要能举出集合M中的一个x0,使得p(x0)不成立即可.
(2)要判定一个存在量词命题是真命题,只要在限定集合M中,能找到一个x0使p(x0)成立即可;否则,这个存在量词命题就是假命题.
活学活用
2.指出下列命题是全称量词命题,还是存在量词命题,并判断真假.
(1) ?x∈R ,x2-x+1=0
(2)任意两个等边三角形都相似;
(3)有些平行四边形是菱形;
(4)?x0∈R,使????02+1<0.
?
全称量词命题
假
全称量词命题
真
存在量词命题
存在量词命题
真
假
达标检测
1.下列命题中,真命题是( )
A.?x0∈R,????????0≤0
B.?x∈R,2x>x2
C.a+b=0的充要条件是????????=-1
D.a>1,b>1是ab>1的充分条件
?
D
假
?x∈R,ex>0
当x=2时,2x=x2
假
b可取0
b不可取0
假
真
本课小结
1.判断全称命题真假的步骤为“先找反例后证明”.
2.判断特称命题真假的步骤为“先找正例后证明”.
