14.1.4整式的乘法(第4课时) 课件(共32张PPT)
文档属性
| 名称 | 14.1.4整式的乘法(第4课时) 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
14.1.4整式的乘法(第4课时)
人教版 八年级上册
教学目标
【教学目标】
1. 掌握同底数幂除法的运算法则并能正确计算.
2. 知道任何不等于0的数的0次幂都等于1.
3. 掌握单项式除以单项式及多项式除以单项式的运算法则并能正确计算.
【重点】同底数幂的除法法则,单项式除以单项式及多项式除以单项式的运算法则.
【难点】同底数幂的除法运算,单项式或多项式除以单项式的运算.
回顾复习
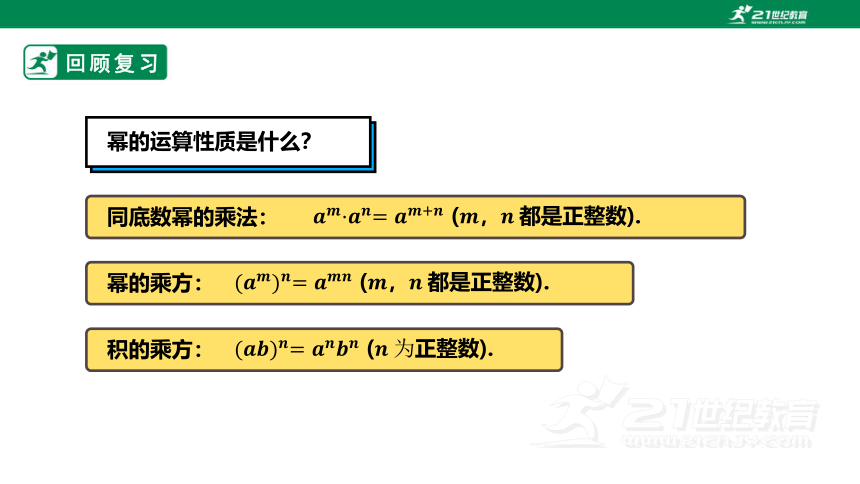
幂的运算性质是什么?
同底数幂的乘法:
幂的乘方:
积的乘方:
(,都是正整数).
(,都是正整数).
(正整数).
新知探究
2.填空
(1) ( ) 22 29 (2) ( )·a2 a7 (3) ( ) 5n 5m n
(m,n是正整数)
除法是乘法的逆运算
1.计算:
(1) 27 22 (2) a5·a2 (3) 5m 5n
(m,n是正整数)
29
a7
5m n
27
a5
5m
(1) 29 22 ( ) (2) a7 a2 ( ) (3) 5m n 5n ( )
(m,n是正整数)
27
a5
5m
观察计算过程,你能发现什么规律?
(a 0)
(a 0)
新知探究
(1) 29 22 ( )
(2) a7 a2 ( )
(3) 5m n 5n ( )
(m,n是正整数)
27
a5
5m
观察计算过程,你能发现什么规律?
9 2 7
7 2 5
(m n) n 5
1.都是同底数幂的除法;
2.底数不变,
指数相减.
(a 0,m,n是正整数,m n )
你能用式子表示这个规律吗?
验证:因为am-n ·an=am-n+n=am,所以am ÷an=am-n.
猜想
新知探究
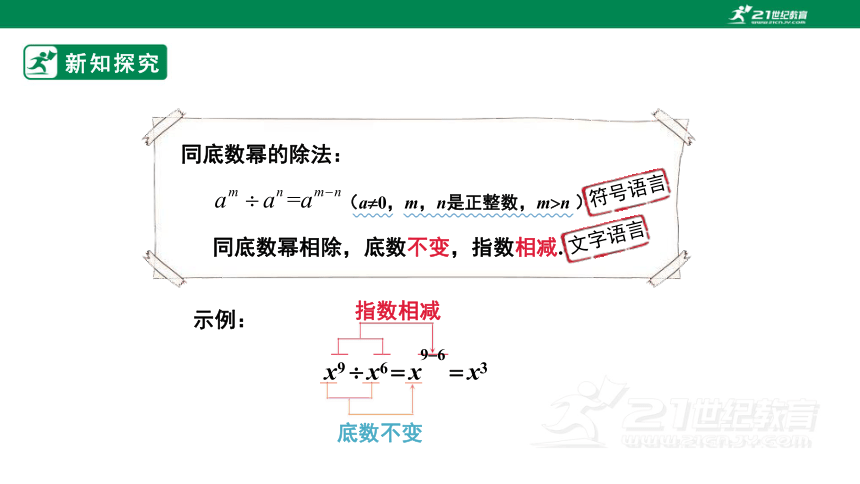
同底数幂的除法:
同底数幂相除,底数不变,指数相减.
(a 0,m,n是正整数,m n )
符号语言
文字语言
x9 x6
示例:
x
x3
底数不变
指数相减
9 6
新知探究
例7 计算:
(1)x8 ÷x2 ; (2) (ab)5 ÷(ab)2.
解:(1)x8 ÷x2=x8-2=x6;
(2) (ab)5 ÷(ab)2=(ab)5-2=(ab)3=a3b3.
方法总结:计算同底数幂的除法时,先判断底数是否相同或变形为相同,若底数为多项式,可将其看作一个整体,再根据法则计算.
新知探究
零指数的意义:
若am÷am,那么,按照公式,am÷an=am-m=a0.
但是,根据除法的意义,am÷am=1,可见:
a0=1(a≠0)
我们规定,任何数的0次幂等于1,0的0次幂无意义.
针对训练
分析:分别利用绝对值的意义和零指数幂的定义计算各自的值,再把结果相加.
解:原式=3+1=4.
(1)零指数幂在同底数幂除法中,是除式与被除式的指
数相同时的特殊情况.
(2)指数为0,但底数不能为0,因为底数为0时,除法无意义.
计算:
新知探究
探究:计算:12a3b2x3÷3ab2.
问题:(1)这是单项式除以单项式吗?怎样求解?
(2)同底数幂的除法我们是运用了乘法的逆运算来计算,单项式除以单项式可不可以用同样的方法来计算?
(3)观察式子12a3b2x3÷3ab2=4a2x3,等式左右两边的数字因数有什么关系,相同字母的指数有什么关系?只在被除数中含有的字母,前后有没有变化?
(4)你能归纳出单项式除以单项式法则吗?
新知探究
单项式除以单项式的运算法则
单项式相除,把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
针对训练
1.下列计算错在哪里?怎样改正?
(1)4a8 ÷2a 2= 2a 4 ( )
(2)10a3 ÷5a2=5a ( )
(3)(-9x5) ÷(-3x) =-3x4 ( )
(4)12a3b ÷4a2=3a ( )
2a6
2a
3x4
7ab
×
×
×
×
系数相除
同底数幂的除法,底数不变,指数相减
只在一个被除式里含有的字母,要连同它的指数写在商里,防止遗漏.
求商的系数,应注意符号
针对训练
2.计算
(1)(2a2b2c)4z÷(-2ab2c2)2; (2)(3x3y3z)4÷(3x3y2z)2÷x2y6z.
解:(1)原式=16a8b8c4z÷4a2b4c4=4a6b4z;
(2)原式=81x12y12z4÷9x6y4z2÷x2y6z=9x4y2z.
新知探究
单项式除以单项式的“三注意”:
(1)系数相除作为商的系数,系数包括前面的符号,应先确定
商的符号;
(2)含有相同字母的部分按同底数幂的除法法则进行运算,即
底数不变,指数相减;
(3)单独在被除式中出现的字母不能漏掉,要连同它的指数直
接作为商的一个因式.
新知探究
?
.
.
,
.
分析
多项式除以单项式
新知探究
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
多项式除以单项式的运算法则
新知探究
多项式除以单项式的“四注意”
(1)多项式除以单项式要转化为单项式除以单项式;
(2)多项式是几项,所得的商就有几项;
(3)要注意商的符号,应弄清多项式中每一项的符号,相除时
要带着符号与单项式相除,注意符号的变化;
(4)注意运算顺序.
新知探究
(1)28x4y2 ÷7x3y;
(2)-5a5b3c ÷15a4b.
=4xy;
(2)原式=(-5÷15)a5-4b3-1c
解:(1)原式=(28 ÷7)x4-3y2-1
= ab2c.
例8 计算
解:
新知探究
整式的混合运算和有理数的混合运算类似,先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
针对训练
分析:先算括号内的,再做除法运算.
解:原式=(3a2+8ab+4b2-4ab-4b2)÷2a
=(3a2+4ab)÷2a
=
计算:[(3a+2b)(a+2b)-b(4a+4b)]÷2a .
课堂练习
1. 下列算式中,正确的有( )
① x8 x2 x4; ② ( a)4 ( a) a3;
③ (x2)3 (x3)2 0; ④ x9 x5 x4 1.
A. 1个 B. 2个 C.3个 D.4个
解:
① x8 x2 x8 2 x6;
② ( a)4 ( a) ( a)4 1 ( a)3
(3) (x2)3 (x3)2 x6 x6 1;
(4) x9 x5 x4 x9 5 4 1.
a3;
A
2.计算-12a6÷3a2的结果是( )
A.-4a3 B.-4a8
C.-4a4 D.- a4
课堂练习
C
3.下列运算结果正确的是( )
A.a+2b=3ab B.3a2-2a2=1
C.a2·a4=a8 D.(-a2b)3÷(a3b)2=-b
D
课堂练习
4.计算多项式-2x(3x-2)2+3除以3x-2后,所得商式与余式两者之和为何?( )
A.-2x+3 B.-6x2+4x
C.-6x2+4x+3 D.-6x2-4x+3
C
课堂练习
5.下列计算:
①(6ab+5a)÷a=6b+5,
②(8x2y-4xy2)÷(-4xy)=-2x-y,
③(15x2yz-10xy2)÷5xy=3x-2y,
④(3x2y-3xy2+x)÷x=3xy-3y2.
其中不正确的有( )
A.1个 B.2个 C.3个 D.4个
C
课堂练习
6.已知(2x 3)0 1,则x的取值范围是 .
解:
由题意知:2x 3 0
∴x
x
7.已知xm 4,xn 9,求x3m 2n的值.
解:
x3m 2n x3m x2n
(xm)3 (xn)2
把xm 4,xn 9代入上式可得:
x3m 2n 43 92
课堂练习
解:
课堂练习
9.(1)若32 92x+1÷27x+1=81,求x的值;
解:(1)32 34x+2÷33x+3=81,
即 3x+1=34,
解得x=3;
(3)已知2x-5y-4=0,求4x÷32y的值.
(3)∵2x-5y-4=0,移项,得2x-5y=4.
4x÷32y=22x÷25y=22x-5y=24=16.
(2) 已知5x=36,5y=2,求5x-2y的值;
(2)52y=(5y)2=4,
5x-2y=5x÷52y=36÷4=9.
课堂练习
10.若一个长方形的面积为,宽为则长方形的长为多少?
解:
课堂小结
同底数幂的除法法则
1
零次幂
2
任何不等于的数的次幂都等于.
.
同底数幂相除,底数不变,指数相减.
都是正整数.
课堂小结
单项式除以单项式法则
3
多项式除以单项式法则
4
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
单项式相除,把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
14.1.4整式的乘法(第4课时)
人教版 八年级上册
教学目标
【教学目标】
1. 掌握同底数幂除法的运算法则并能正确计算.
2. 知道任何不等于0的数的0次幂都等于1.
3. 掌握单项式除以单项式及多项式除以单项式的运算法则并能正确计算.
【重点】同底数幂的除法法则,单项式除以单项式及多项式除以单项式的运算法则.
【难点】同底数幂的除法运算,单项式或多项式除以单项式的运算.
回顾复习
幂的运算性质是什么?
同底数幂的乘法:
幂的乘方:
积的乘方:
(,都是正整数).
(,都是正整数).
(正整数).
新知探究
2.填空
(1) ( ) 22 29 (2) ( )·a2 a7 (3) ( ) 5n 5m n
(m,n是正整数)
除法是乘法的逆运算
1.计算:
(1) 27 22 (2) a5·a2 (3) 5m 5n
(m,n是正整数)
29
a7
5m n
27
a5
5m
(1) 29 22 ( ) (2) a7 a2 ( ) (3) 5m n 5n ( )
(m,n是正整数)
27
a5
5m
观察计算过程,你能发现什么规律?
(a 0)
(a 0)
新知探究
(1) 29 22 ( )
(2) a7 a2 ( )
(3) 5m n 5n ( )
(m,n是正整数)
27
a5
5m
观察计算过程,你能发现什么规律?
9 2 7
7 2 5
(m n) n 5
1.都是同底数幂的除法;
2.底数不变,
指数相减.
(a 0,m,n是正整数,m n )
你能用式子表示这个规律吗?
验证:因为am-n ·an=am-n+n=am,所以am ÷an=am-n.
猜想
新知探究
同底数幂的除法:
同底数幂相除,底数不变,指数相减.
(a 0,m,n是正整数,m n )
符号语言
文字语言
x9 x6
示例:
x
x3
底数不变
指数相减
9 6
新知探究
例7 计算:
(1)x8 ÷x2 ; (2) (ab)5 ÷(ab)2.
解:(1)x8 ÷x2=x8-2=x6;
(2) (ab)5 ÷(ab)2=(ab)5-2=(ab)3=a3b3.
方法总结:计算同底数幂的除法时,先判断底数是否相同或变形为相同,若底数为多项式,可将其看作一个整体,再根据法则计算.
新知探究
零指数的意义:
若am÷am,那么,按照公式,am÷an=am-m=a0.
但是,根据除法的意义,am÷am=1,可见:
a0=1(a≠0)
我们规定,任何数的0次幂等于1,0的0次幂无意义.
针对训练
分析:分别利用绝对值的意义和零指数幂的定义计算各自的值,再把结果相加.
解:原式=3+1=4.
(1)零指数幂在同底数幂除法中,是除式与被除式的指
数相同时的特殊情况.
(2)指数为0,但底数不能为0,因为底数为0时,除法无意义.
计算:
新知探究
探究:计算:12a3b2x3÷3ab2.
问题:(1)这是单项式除以单项式吗?怎样求解?
(2)同底数幂的除法我们是运用了乘法的逆运算来计算,单项式除以单项式可不可以用同样的方法来计算?
(3)观察式子12a3b2x3÷3ab2=4a2x3,等式左右两边的数字因数有什么关系,相同字母的指数有什么关系?只在被除数中含有的字母,前后有没有变化?
(4)你能归纳出单项式除以单项式法则吗?
新知探究
单项式除以单项式的运算法则
单项式相除,把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
针对训练
1.下列计算错在哪里?怎样改正?
(1)4a8 ÷2a 2= 2a 4 ( )
(2)10a3 ÷5a2=5a ( )
(3)(-9x5) ÷(-3x) =-3x4 ( )
(4)12a3b ÷4a2=3a ( )
2a6
2a
3x4
7ab
×
×
×
×
系数相除
同底数幂的除法,底数不变,指数相减
只在一个被除式里含有的字母,要连同它的指数写在商里,防止遗漏.
求商的系数,应注意符号
针对训练
2.计算
(1)(2a2b2c)4z÷(-2ab2c2)2; (2)(3x3y3z)4÷(3x3y2z)2÷x2y6z.
解:(1)原式=16a8b8c4z÷4a2b4c4=4a6b4z;
(2)原式=81x12y12z4÷9x6y4z2÷x2y6z=9x4y2z.
新知探究
单项式除以单项式的“三注意”:
(1)系数相除作为商的系数,系数包括前面的符号,应先确定
商的符号;
(2)含有相同字母的部分按同底数幂的除法法则进行运算,即
底数不变,指数相减;
(3)单独在被除式中出现的字母不能漏掉,要连同它的指数直
接作为商的一个因式.
新知探究
?
.
.
,
.
分析
多项式除以单项式
新知探究
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
多项式除以单项式的运算法则
新知探究
多项式除以单项式的“四注意”
(1)多项式除以单项式要转化为单项式除以单项式;
(2)多项式是几项,所得的商就有几项;
(3)要注意商的符号,应弄清多项式中每一项的符号,相除时
要带着符号与单项式相除,注意符号的变化;
(4)注意运算顺序.
新知探究
(1)28x4y2 ÷7x3y;
(2)-5a5b3c ÷15a4b.
=4xy;
(2)原式=(-5÷15)a5-4b3-1c
解:(1)原式=(28 ÷7)x4-3y2-1
= ab2c.
例8 计算
解:
新知探究
整式的混合运算和有理数的混合运算类似,先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
针对训练
分析:先算括号内的,再做除法运算.
解:原式=(3a2+8ab+4b2-4ab-4b2)÷2a
=(3a2+4ab)÷2a
=
计算:[(3a+2b)(a+2b)-b(4a+4b)]÷2a .
课堂练习
1. 下列算式中,正确的有( )
① x8 x2 x4; ② ( a)4 ( a) a3;
③ (x2)3 (x3)2 0; ④ x9 x5 x4 1.
A. 1个 B. 2个 C.3个 D.4个
解:
① x8 x2 x8 2 x6;
② ( a)4 ( a) ( a)4 1 ( a)3
(3) (x2)3 (x3)2 x6 x6 1;
(4) x9 x5 x4 x9 5 4 1.
a3;
A
2.计算-12a6÷3a2的结果是( )
A.-4a3 B.-4a8
C.-4a4 D.- a4
课堂练习
C
3.下列运算结果正确的是( )
A.a+2b=3ab B.3a2-2a2=1
C.a2·a4=a8 D.(-a2b)3÷(a3b)2=-b
D
课堂练习
4.计算多项式-2x(3x-2)2+3除以3x-2后,所得商式与余式两者之和为何?( )
A.-2x+3 B.-6x2+4x
C.-6x2+4x+3 D.-6x2-4x+3
C
课堂练习
5.下列计算:
①(6ab+5a)÷a=6b+5,
②(8x2y-4xy2)÷(-4xy)=-2x-y,
③(15x2yz-10xy2)÷5xy=3x-2y,
④(3x2y-3xy2+x)÷x=3xy-3y2.
其中不正确的有( )
A.1个 B.2个 C.3个 D.4个
C
课堂练习
6.已知(2x 3)0 1,则x的取值范围是 .
解:
由题意知:2x 3 0
∴x
x
7.已知xm 4,xn 9,求x3m 2n的值.
解:
x3m 2n x3m x2n
(xm)3 (xn)2
把xm 4,xn 9代入上式可得:
x3m 2n 43 92
课堂练习
解:
课堂练习
9.(1)若32 92x+1÷27x+1=81,求x的值;
解:(1)32 34x+2÷33x+3=81,
即 3x+1=34,
解得x=3;
(3)已知2x-5y-4=0,求4x÷32y的值.
(3)∵2x-5y-4=0,移项,得2x-5y=4.
4x÷32y=22x÷25y=22x-5y=24=16.
(2) 已知5x=36,5y=2,求5x-2y的值;
(2)52y=(5y)2=4,
5x-2y=5x÷52y=36÷4=9.
课堂练习
10.若一个长方形的面积为,宽为则长方形的长为多少?
解:
课堂小结
同底数幂的除法法则
1
零次幂
2
任何不等于的数的次幂都等于.
.
同底数幂相除,底数不变,指数相减.
都是正整数.
课堂小结
单项式除以单项式法则
3
多项式除以单项式法则
4
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
单项式相除,把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
