人教B版(2019)数学必修第一册1.1.1.1 集合的含义 课件(共32张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册1.1.1.1 集合的含义 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
1.1.1.1 集合的含义
高一
必修一
情景引入
集合
本节目标
1.通过实例了解集合的含义,并掌握集合中元素的三个特性.
2.体会元素与集合间的“从属关系”.
3.记住常用数集的表示符号并会应用.
任务一:知识预习
课前预习
(1)集合和元素的含义是什么?它们各自用什么字母表示?
(2)元素和集合之间有哪两种关系?常见的数集有哪些?分别用什么符号表示?
预习课本,思考并完成以下问题
任务二:简单题型通关
课前预习
1.判断(正确的打“√”,错误的打“×”)
(1)你班所有的姓氏能组成集合. ( )
(2)新课标数学人教A版必修1课本上的所有难题.( )
(3)一个集合中可以找到两个相同的元素. ( )
√
×
×
标准不明确
集合的元素具有互异性
课前预习
2.下列元素与集合的关系判断正确的是( )
A.0∈N B.π∈Q
C. ∈Q D.-1 Z
A
课前预习
3.已知集合A中含有两个元素1,x2,且x∈A,则x的值是( )
A.0 B.1
C.-1 D.0或1
A
x=1
x=x2
x∈A
x=0或1
集合A中的两个元素1,1
×
x=0时集合A中的两个元素1,0
√
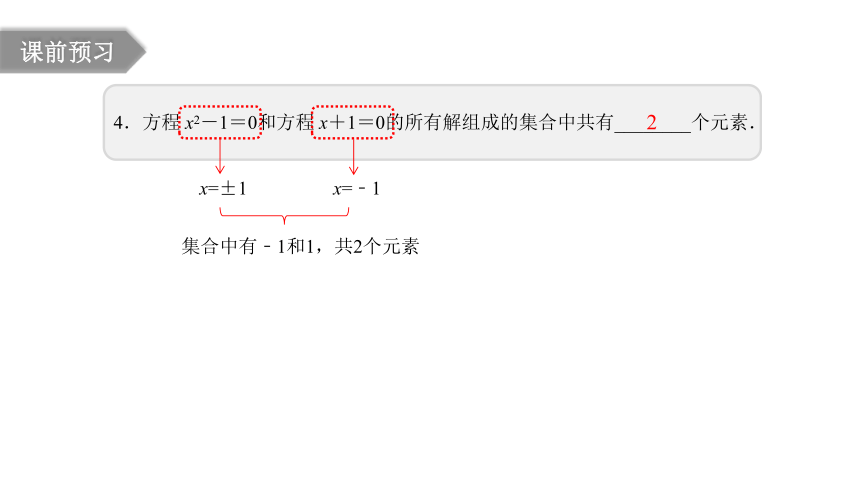
4.方程 x2-1=0和方程 x+1=0的所有解组成的集合中共有________个元素.
课前预习
x=±1
x=﹣1
集合中有﹣1和1,共2个元素
2
新知精讲
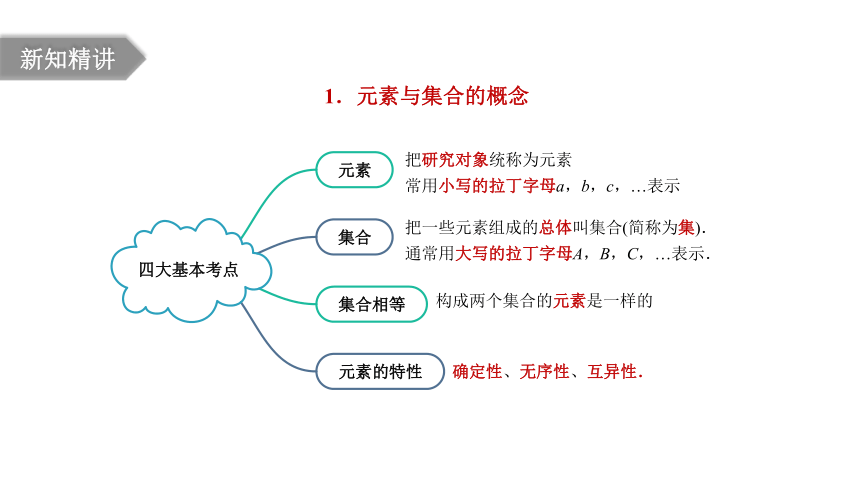
1.元素与集合的概念
四大基本考点
元素
集合
集合相等
元素的特性
把研究对象统称为元素
常用小写的拉丁字母a,b,c,…表示
把一些元素组成的总体叫集合(简称为集).
通常用大写的拉丁字母A,B,C,…表示.
构成两个集合的元素是一样的
确定性、无序性、互异性.
新知精讲
知
识
点
睛
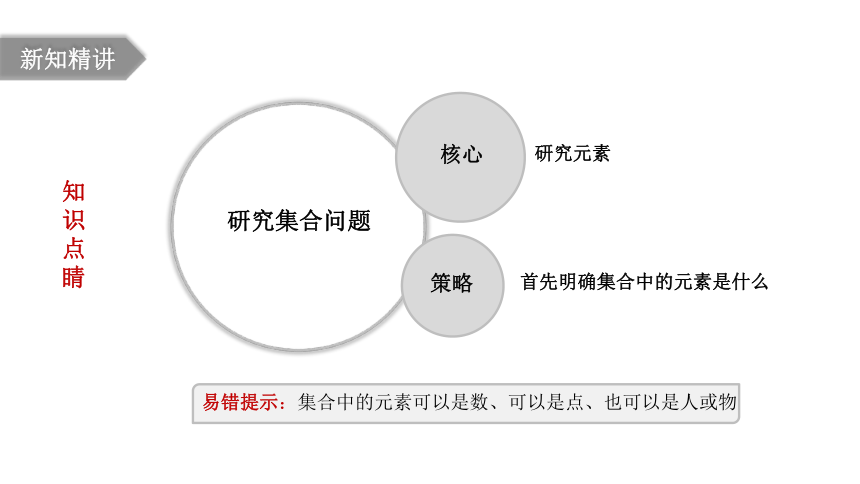
研究集合问题
核心
研究元素
策略
首先明确集合中的元素是什么
易错提示:集合中的元素可以是数、可以是点、也可以是人或物
新知精讲
3.元素与集合的关系
关系 语言描述 记法 读法
属于 a是集合A中的元素 aA a属于集合A
不属于 a不是集合A中的元素 a A a不属于集合A
[易错提示]
符号“”“”刻画的是元素与集合之间的关系.对于一个元素a与一个集合A而言,只有“a∈A”与“a A”这两种结果.
和具有方向性,左边是元素,右边是集合,例如R∈0是错误的.
新知精讲
3.常用的数集及其记法
常用的数集 自然数集 正整数集 整数集 有理数集 实数集
记法 N N*或N+ Z Q R
题型探究
题型一 集合的基本概念
例1 下列各组对象,能构成一个集合的是( )
①某校高一年级成绩优秀的学生;
②直角坐标系中横、纵坐标相等的点;
③不小于3的自然数;
④2018年第23届冬季奥运会金牌获得者.
A.③④ B.②③④
C.②③ D.②④
没有明确的标准
×
√
√
√
B
归纳总结
判断一组对象能否构成集合的方法
关键看该组对象是否满足确定性,如果满足,就可以构成集合;否则,不能构成集合.
还要注意集合中元素的互异性、无序性.
活学活用
1.给出下列说法:
①中国的所有直辖市可以构成一个集合;
②高一(1)班较胖的同学可以构成一个集合;
③正偶数的全体可以构成一个集合;
④大于2013且小于2018的所有整数不能构成集合.
其中正确的有________.(填序号)
√
没有明确的标准
×
√
×
标准明确可以构成集合
①
③
题型探究
题型二 元素与集合的关系
例2 下列关系中,正确的有( )
①∈R; ② Q; ③|-3|∈N; ④|-|∈Q.
A.1个 B.2个 C.3个 D.4个
√
×
√
√
实数
有理数
自然数
不是有理数
C
题型探究
题型二 元素与集合的关系
例3 集合A中的元素x满足∈N,x∈N,则集合A中的元素为________.
3-x可以为1,2,3,6
x∈N
x的值为2,1,0
A中元素有2,1,0
2,1,0
归纳总结
判断
元素与集合关系
的2种方法
①直接法
②推理法
如果集合中元素是直接给出,只要判断该元素在已知集合中是否出现即可
对于没有直接表示的集合,只要判断该元素是否满足集合中元素所具有的特征即可
应首先明确已知集合中的元素具有什么特征
活学活用
2.已知集合A中有四个元素0,1,2,3,集合B中有三个元素0,1,2,且元素 a∈A,a B,则a的值为( )
A.0 B.1 C.2 D.3
D
3
活学活用
3.用适当的符号填空:
已知A={x|x=3k+2,k∈Z},B={x|x=6m-1,m∈Z},则有:17________A;-5________A;17________B.
令3k+2=17
k=5∈Z
令3k+2=-5
k=- Z
令6m-1=17
m=3∈Z
∈
∈
题型探究
题型三 集合中元素的特性及应用
一题多变
发散思维
例4 已知集合A含有两个元素 a和a2,若1∈A,则实数a的值为________.
a=1或a2=1
a=±1
a=1时,集合A有重复元素
a=-1时,集合A有两个元素1,-1
a=-1
不符合
互异性
-1
题型探究
题型三 集合中元素的特性及应用
一题多变
发散思维
例4 已知集合A含有两个元素 a和a2,若1∈A,则实数a的值为_________.
改为2∈A
2∈A
a=2或a2=2
a=2,或a=,或a=-
经检验均满足元素的互异性
2, ,-
题型探究
题型三 集合中元素的特性及应用
一题多变
发散思维
例4 已知集合A含有两个元素 a和a2,若1∈A,则实数a的取值范围是什么?
A中有两个元素a和a2
a≠a2
a≠0且a≠1
删掉
题型探究
题型三 集合中元素的特性及应用
一题多变
发散思维
例4 已知集合A含有两个元素 a和a2,若1∈A,求实数a的值.
a∈A
a=1时, a2=1
与集合元素的互异性矛盾
a≠1
a=a2时
a=0
a=0或1(舍去)
改为:1和a2,若a∈A
归纳总结
根据集合中元素的特性求解字母取值(范围)的3个步骤
易错误区
忽略集合元素中的互异性而出错
例5 含有三个元素的集合也可表示为集合{a2,a+b,0},求a,b的值.
={a2,a+b,0}
或
易错提示:到这里没有结束,要检验是否满足互异性
由集合中元素的互异性,得a≠1
a=-1,b=0
易错总结
易错警示
错误
原因
纠错
心得
忽略了集合中元素的互异性,当a=1时,在一个集合中出现了两个相同的元素.
含有参数的集合问题,涉及的内容多为元素与集合的关系、集合相等,解题时需要根据集合中元素的互异性对参数的取值进行分类讨论.
达标检测
1.下列各组集合,表示相等集合的是( )
①M={(3,2)},N={(2,3)};
②M={3,2},N={2,3};
③M={(1,2)},N={1,2}.
A.① B.② C.③ D.以上都不对
点(3,2)与点(2,3)是两个不同的点
元素的无序性
×
√
M有一个元素点(1,2),N有两个元素1,2
×
B
达标检测
2.已知集合M={1,a},则实数a满足的条件是( )
A.a∈R B.a∈Q
C.a=1 D.a≠1
元素的互异性
M={1,a}
a≠1
D
达标检测
3.集合{x∈N|2x-5<0}中所有元素的和为________.
2x-5<0
x<
x∈N
x=0,1,2
元素之和为3
3
达标检测
4.已知集合A={x|x2+px+q=0}={2},则p+q=________.
x2+px+q=0有两个相等的实根
p+q=0
0
本课小结
研究对象能否构成集合,就要看是否有一个确定的标准,能确定一个个体是否属于这个总体.
集合元素的三个特征
①确定性:给定的集合,它的元素必须是确定的
②互异性:给定的集合,它的任何两个元素都是不同的
③无序性:集合中元素没有顺序
1.1.1.1 集合的含义
高一
必修一
情景引入
集合
本节目标
1.通过实例了解集合的含义,并掌握集合中元素的三个特性.
2.体会元素与集合间的“从属关系”.
3.记住常用数集的表示符号并会应用.
任务一:知识预习
课前预习
(1)集合和元素的含义是什么?它们各自用什么字母表示?
(2)元素和集合之间有哪两种关系?常见的数集有哪些?分别用什么符号表示?
预习课本,思考并完成以下问题
任务二:简单题型通关
课前预习
1.判断(正确的打“√”,错误的打“×”)
(1)你班所有的姓氏能组成集合. ( )
(2)新课标数学人教A版必修1课本上的所有难题.( )
(3)一个集合中可以找到两个相同的元素. ( )
√
×
×
标准不明确
集合的元素具有互异性
课前预习
2.下列元素与集合的关系判断正确的是( )
A.0∈N B.π∈Q
C. ∈Q D.-1 Z
A
课前预习
3.已知集合A中含有两个元素1,x2,且x∈A,则x的值是( )
A.0 B.1
C.-1 D.0或1
A
x=1
x=x2
x∈A
x=0或1
集合A中的两个元素1,1
×
x=0时集合A中的两个元素1,0
√
4.方程 x2-1=0和方程 x+1=0的所有解组成的集合中共有________个元素.
课前预习
x=±1
x=﹣1
集合中有﹣1和1,共2个元素
2
新知精讲
1.元素与集合的概念
四大基本考点
元素
集合
集合相等
元素的特性
把研究对象统称为元素
常用小写的拉丁字母a,b,c,…表示
把一些元素组成的总体叫集合(简称为集).
通常用大写的拉丁字母A,B,C,…表示.
构成两个集合的元素是一样的
确定性、无序性、互异性.
新知精讲
知
识
点
睛
研究集合问题
核心
研究元素
策略
首先明确集合中的元素是什么
易错提示:集合中的元素可以是数、可以是点、也可以是人或物
新知精讲
3.元素与集合的关系
关系 语言描述 记法 读法
属于 a是集合A中的元素 aA a属于集合A
不属于 a不是集合A中的元素 a A a不属于集合A
[易错提示]
符号“”“”刻画的是元素与集合之间的关系.对于一个元素a与一个集合A而言,只有“a∈A”与“a A”这两种结果.
和具有方向性,左边是元素,右边是集合,例如R∈0是错误的.
新知精讲
3.常用的数集及其记法
常用的数集 自然数集 正整数集 整数集 有理数集 实数集
记法 N N*或N+ Z Q R
题型探究
题型一 集合的基本概念
例1 下列各组对象,能构成一个集合的是( )
①某校高一年级成绩优秀的学生;
②直角坐标系中横、纵坐标相等的点;
③不小于3的自然数;
④2018年第23届冬季奥运会金牌获得者.
A.③④ B.②③④
C.②③ D.②④
没有明确的标准
×
√
√
√
B
归纳总结
判断一组对象能否构成集合的方法
关键看该组对象是否满足确定性,如果满足,就可以构成集合;否则,不能构成集合.
还要注意集合中元素的互异性、无序性.
活学活用
1.给出下列说法:
①中国的所有直辖市可以构成一个集合;
②高一(1)班较胖的同学可以构成一个集合;
③正偶数的全体可以构成一个集合;
④大于2013且小于2018的所有整数不能构成集合.
其中正确的有________.(填序号)
√
没有明确的标准
×
√
×
标准明确可以构成集合
①
③
题型探究
题型二 元素与集合的关系
例2 下列关系中,正确的有( )
①∈R; ② Q; ③|-3|∈N; ④|-|∈Q.
A.1个 B.2个 C.3个 D.4个
√
×
√
√
实数
有理数
自然数
不是有理数
C
题型探究
题型二 元素与集合的关系
例3 集合A中的元素x满足∈N,x∈N,则集合A中的元素为________.
3-x可以为1,2,3,6
x∈N
x的值为2,1,0
A中元素有2,1,0
2,1,0
归纳总结
判断
元素与集合关系
的2种方法
①直接法
②推理法
如果集合中元素是直接给出,只要判断该元素在已知集合中是否出现即可
对于没有直接表示的集合,只要判断该元素是否满足集合中元素所具有的特征即可
应首先明确已知集合中的元素具有什么特征
活学活用
2.已知集合A中有四个元素0,1,2,3,集合B中有三个元素0,1,2,且元素 a∈A,a B,则a的值为( )
A.0 B.1 C.2 D.3
D
3
活学活用
3.用适当的符号填空:
已知A={x|x=3k+2,k∈Z},B={x|x=6m-1,m∈Z},则有:17________A;-5________A;17________B.
令3k+2=17
k=5∈Z
令3k+2=-5
k=- Z
令6m-1=17
m=3∈Z
∈
∈
题型探究
题型三 集合中元素的特性及应用
一题多变
发散思维
例4 已知集合A含有两个元素 a和a2,若1∈A,则实数a的值为________.
a=1或a2=1
a=±1
a=1时,集合A有重复元素
a=-1时,集合A有两个元素1,-1
a=-1
不符合
互异性
-1
题型探究
题型三 集合中元素的特性及应用
一题多变
发散思维
例4 已知集合A含有两个元素 a和a2,若1∈A,则实数a的值为_________.
改为2∈A
2∈A
a=2或a2=2
a=2,或a=,或a=-
经检验均满足元素的互异性
2, ,-
题型探究
题型三 集合中元素的特性及应用
一题多变
发散思维
例4 已知集合A含有两个元素 a和a2,若1∈A,则实数a的取值范围是什么?
A中有两个元素a和a2
a≠a2
a≠0且a≠1
删掉
题型探究
题型三 集合中元素的特性及应用
一题多变
发散思维
例4 已知集合A含有两个元素 a和a2,若1∈A,求实数a的值.
a∈A
a=1时, a2=1
与集合元素的互异性矛盾
a≠1
a=a2时
a=0
a=0或1(舍去)
改为:1和a2,若a∈A
归纳总结
根据集合中元素的特性求解字母取值(范围)的3个步骤
易错误区
忽略集合元素中的互异性而出错
例5 含有三个元素的集合也可表示为集合{a2,a+b,0},求a,b的值.
={a2,a+b,0}
或
易错提示:到这里没有结束,要检验是否满足互异性
由集合中元素的互异性,得a≠1
a=-1,b=0
易错总结
易错警示
错误
原因
纠错
心得
忽略了集合中元素的互异性,当a=1时,在一个集合中出现了两个相同的元素.
含有参数的集合问题,涉及的内容多为元素与集合的关系、集合相等,解题时需要根据集合中元素的互异性对参数的取值进行分类讨论.
达标检测
1.下列各组集合,表示相等集合的是( )
①M={(3,2)},N={(2,3)};
②M={3,2},N={2,3};
③M={(1,2)},N={1,2}.
A.① B.② C.③ D.以上都不对
点(3,2)与点(2,3)是两个不同的点
元素的无序性
×
√
M有一个元素点(1,2),N有两个元素1,2
×
B
达标检测
2.已知集合M={1,a},则实数a满足的条件是( )
A.a∈R B.a∈Q
C.a=1 D.a≠1
元素的互异性
M={1,a}
a≠1
D
达标检测
3.集合{x∈N|2x-5<0}中所有元素的和为________.
2x-5<0
x<
x∈N
x=0,1,2
元素之和为3
3
达标检测
4.已知集合A={x|x2+px+q=0}={2},则p+q=________.
x2+px+q=0有两个相等的实根
p+q=0
0
本课小结
研究对象能否构成集合,就要看是否有一个确定的标准,能确定一个个体是否属于这个总体.
集合元素的三个特征
①确定性:给定的集合,它的元素必须是确定的
②互异性:给定的集合,它的任何两个元素都是不同的
③无序性:集合中元素没有顺序
