人教B版(2019)数学必修第一册1.2.2 全称量词命题与存在量词命题的否定 课件(共18张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册1.2.2 全称量词命题与存在量词命题的否定 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 464.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 15:42:51 | ||
图片预览





文档简介
(共18张PPT)
1.2.3 全称量词命题与存在量词命题的否定
高一
必修一
本节目标
1.能正确地对含有一个量词的命题进行否定.
2.体会从具体到一般的认知过程,培养抽象、概括的能力.
任务一:知识预习
课前预习
预习课本,思考并完成以下问题
1.全称量词命题与存在量词命题的分别是什么?
2.全称量词命题与存在量词命题的否定分别是什么命题?
课前预习
1.命题“ x∈R,|x|+x2≥0”的否定是( )
A. x∈R,|x|+x2<0 B. x∈R,|x|+x2≤0
C. x0∈R,|x0|+<0 D. x0∈R,|x0|+≥0
任务二:简单题型通关
C
课前预习
任务二:简单题型通关
2.命题p: x0∈R,+2x0+5<0是____________(填“全称量词命题”或“存在量词命题”),它是______命题(填“真”或“假”),它的否定为 p:___________________.
存在量词命题
假
x∈R,x2+2x+5≥0
新知精讲
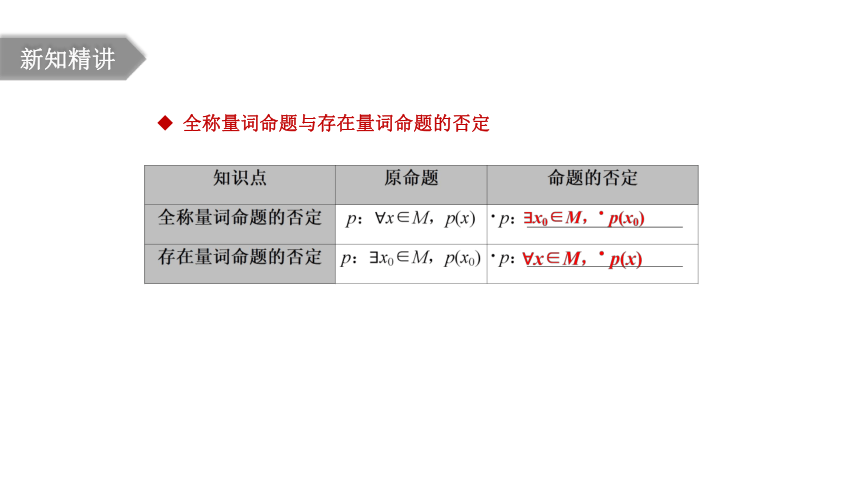
全称量词命题与存在量词命题的否定
新知精讲
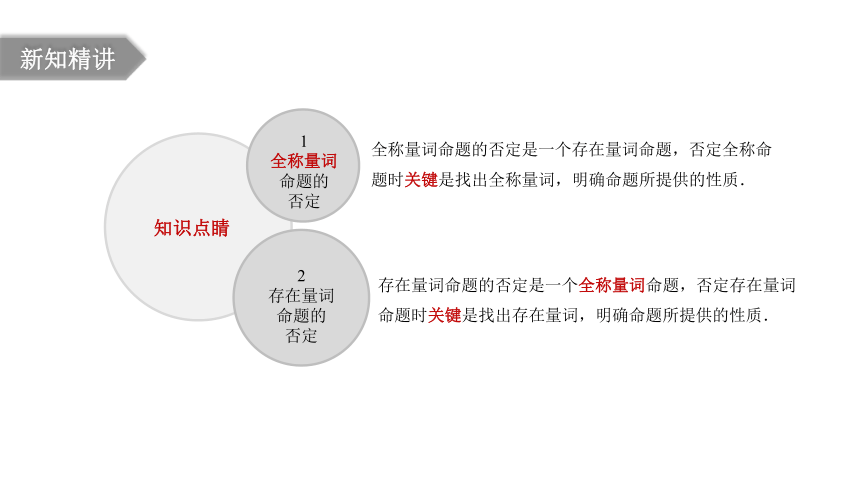
存在量词命题的否定是一个全称量词命题,否定存在量词命题时关键是找出存在量词,明确命题所提供的性质.
知识点睛
1
全称量词命题的
否定
2
存在量词命题的
否定
全称量词命题的否定是一个存在量词命题,否定全称命题时关键是找出全称量词,明确命题所提供的性质.
题型探究
题型一 全称命题和特称命题的否定
例1 设命题p: n∈N,n2>2n,则 p为( )
A. n∈N,n2>2n B. n∈N,n2≤2n
C. n∈N,n2≤2n D. n∈N,n2=2n
C
方法提示:“ x∈M,p(x)”的否定是“ x∈M, p(x)”
题型探究
题型一 全称命题和特称命题的否定
例2 命题“ x∈R, n∈N*,使得n≥x2”的否定形式是( )
A. x∈R, n∈N*,使得n<x2
B. x∈R, n∈N*,使得n<x2
C. x∈R, n∈N*,使得n<x2
D. x∈R, n∈N*,使得n<x2
D
归纳总结
全称命题与特称命题的否定的思路
首先明确这个命题是全称命题还是特称命题
然后找到量词及相应结论
最后把命题中的全称量词改成存在量词,存在量词改成全称量词,同时否定结论
注意:对于省略量词的命题,应先挖掘命题中隐含量词,改写成含量词的完整形式,再依据规则来写出命题的否定.
活学活用
1.判断下列命题的真假,并写出它们的否定
(1)三角形的内角和为180°;
(2)每个二次函数的图象都开口向下;
(3)存在一个四边形不是平行四边形.
真命题
否定:三角形的内角和不全为180°
假命题
否定:存在一个二次函数的图象开口不向下
否定:所有的四边形都是平行四边形
真命题
题型探究
题型二 利用全称命题和特称命题求参数
例3 若命题“ x∈[-1,+∞),x2-2ax+2≥a”是真命题,求实数a的取值范围.
令y=x2-2ax+2
x∈[-1,+∞),ymin≥a恒成立
x∈[-1,+∞),
a∈[-3,1]
法 一
题型探究
题型二 利用全称命题和特称命题求参数
例3 若命题“ x∈[-1,+∞),x2-2ax+2≥a”是真命题,求实数a的取值范围.
法 二
x2-2ax+2-a≥0
令y=x2-2ax+2-a
全称命题转化为 x∈[-1,+∞),y≥0恒成立
Δ≤0或
-3≤a≤1
归纳总结
利用全称命题与特称命题求参数范围的两类题型
全称命题的常见题型是“恒成立”问题
全称命题为真时,意味着命题对应的集合中的每一个元素都具有某种性质,所以利用代入可以体现集合中相应元素的具体性质;也可以根据函数等来解决.
特称命题的常见题型是以适合某种条件的结论“存在”“不存在”
“是否存在”等语句表达.
解答这类问题,一般要先对结论作出肯定存在的假设,然后从肯定的假设出发,结合已知条件进行推理证明,若推出合理的结论,则存在性随之解决;若导致矛盾,则否定了假设.
活学活用
2.已知命题p: x0∈R,使-mx0+1=0,命题q: x∈R,有x2-2x+m>0.若命题q∨(p∧q)为真, p为真,求实数m的取值范围.
1p假、q真
p为真
p为假
p∧q为假
q∨(p∧q)为真
q为真
p为假
x2-mx+1=0无实数解
m2-4<0
-2q为真
4-4m<0
m>1
达标检测
1.命题“存在实数x,使x>1”的否定是( )
A.对任意实数x,都有x>1
B.不存在实数x,使x≤1
C.对任意实数x,都有x≤1
D.存在实数x,使x≤1
C
达标检测
2.设x∈Z,集合A是奇数集,集合B是偶数集.若命题p: x∈A,2x∈B,则( )
A. p: x∈A,2x B B. p: x A,2x B
C. p: x A,2x∈B D. p: x∈A,2x B
D
本课小结
全称命题的否定是一个特称命题,特称命题的否定是一个全称命题.
1.2.3 全称量词命题与存在量词命题的否定
高一
必修一
本节目标
1.能正确地对含有一个量词的命题进行否定.
2.体会从具体到一般的认知过程,培养抽象、概括的能力.
任务一:知识预习
课前预习
预习课本,思考并完成以下问题
1.全称量词命题与存在量词命题的分别是什么?
2.全称量词命题与存在量词命题的否定分别是什么命题?
课前预习
1.命题“ x∈R,|x|+x2≥0”的否定是( )
A. x∈R,|x|+x2<0 B. x∈R,|x|+x2≤0
C. x0∈R,|x0|+<0 D. x0∈R,|x0|+≥0
任务二:简单题型通关
C
课前预习
任务二:简单题型通关
2.命题p: x0∈R,+2x0+5<0是____________(填“全称量词命题”或“存在量词命题”),它是______命题(填“真”或“假”),它的否定为 p:___________________.
存在量词命题
假
x∈R,x2+2x+5≥0
新知精讲
全称量词命题与存在量词命题的否定
新知精讲
存在量词命题的否定是一个全称量词命题,否定存在量词命题时关键是找出存在量词,明确命题所提供的性质.
知识点睛
1
全称量词命题的
否定
2
存在量词命题的
否定
全称量词命题的否定是一个存在量词命题,否定全称命题时关键是找出全称量词,明确命题所提供的性质.
题型探究
题型一 全称命题和特称命题的否定
例1 设命题p: n∈N,n2>2n,则 p为( )
A. n∈N,n2>2n B. n∈N,n2≤2n
C. n∈N,n2≤2n D. n∈N,n2=2n
C
方法提示:“ x∈M,p(x)”的否定是“ x∈M, p(x)”
题型探究
题型一 全称命题和特称命题的否定
例2 命题“ x∈R, n∈N*,使得n≥x2”的否定形式是( )
A. x∈R, n∈N*,使得n<x2
B. x∈R, n∈N*,使得n<x2
C. x∈R, n∈N*,使得n<x2
D. x∈R, n∈N*,使得n<x2
D
归纳总结
全称命题与特称命题的否定的思路
首先明确这个命题是全称命题还是特称命题
然后找到量词及相应结论
最后把命题中的全称量词改成存在量词,存在量词改成全称量词,同时否定结论
注意:对于省略量词的命题,应先挖掘命题中隐含量词,改写成含量词的完整形式,再依据规则来写出命题的否定.
活学活用
1.判断下列命题的真假,并写出它们的否定
(1)三角形的内角和为180°;
(2)每个二次函数的图象都开口向下;
(3)存在一个四边形不是平行四边形.
真命题
否定:三角形的内角和不全为180°
假命题
否定:存在一个二次函数的图象开口不向下
否定:所有的四边形都是平行四边形
真命题
题型探究
题型二 利用全称命题和特称命题求参数
例3 若命题“ x∈[-1,+∞),x2-2ax+2≥a”是真命题,求实数a的取值范围.
令y=x2-2ax+2
x∈[-1,+∞),ymin≥a恒成立
x∈[-1,+∞),
a∈[-3,1]
法 一
题型探究
题型二 利用全称命题和特称命题求参数
例3 若命题“ x∈[-1,+∞),x2-2ax+2≥a”是真命题,求实数a的取值范围.
法 二
x2-2ax+2-a≥0
令y=x2-2ax+2-a
全称命题转化为 x∈[-1,+∞),y≥0恒成立
Δ≤0或
-3≤a≤1
归纳总结
利用全称命题与特称命题求参数范围的两类题型
全称命题的常见题型是“恒成立”问题
全称命题为真时,意味着命题对应的集合中的每一个元素都具有某种性质,所以利用代入可以体现集合中相应元素的具体性质;也可以根据函数等来解决.
特称命题的常见题型是以适合某种条件的结论“存在”“不存在”
“是否存在”等语句表达.
解答这类问题,一般要先对结论作出肯定存在的假设,然后从肯定的假设出发,结合已知条件进行推理证明,若推出合理的结论,则存在性随之解决;若导致矛盾,则否定了假设.
活学活用
2.已知命题p: x0∈R,使-mx0+1=0,命题q: x∈R,有x2-2x+m>0.若命题q∨(p∧q)为真, p为真,求实数m的取值范围.
1
p为真
p为假
p∧q为假
q∨(p∧q)为真
q为真
p为假
x2-mx+1=0无实数解
m2-4<0
-2
4-4m<0
m>1
达标检测
1.命题“存在实数x,使x>1”的否定是( )
A.对任意实数x,都有x>1
B.不存在实数x,使x≤1
C.对任意实数x,都有x≤1
D.存在实数x,使x≤1
C
达标检测
2.设x∈Z,集合A是奇数集,集合B是偶数集.若命题p: x∈A,2x∈B,则( )
A. p: x∈A,2x B B. p: x A,2x B
C. p: x A,2x∈B D. p: x∈A,2x B
D
本课小结
全称命题的否定是一个特称命题,特称命题的否定是一个全称命题.
