人教B版(2019)数学必修第一册2.2.3一元二次不等式的解法 课件(共32张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册2.2.3一元二次不等式的解法 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 15.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 15:48:26 | ||
图片预览










文档简介
(共32张PPT)
2.2.3一元二次不等式的解法
高一
必修一
本节目标
1 .了解一元二次不等式的概念.
2.理解一元二次不等式、一元二次方程与二次函数的关系.
3.会解一元二次不等式.
情景引入
二次函数
与一元二次方程
不等式
任务一:知识预习
课前预习
预习课本,思考并完成以下问题
(1)怎样判断一个不等式是否为一元二次不等式?
(2)如何求解一元二次不等式?
(3)三个“二次”指的是哪三个“二次”?它们之间有何关系?
课前预习
任务二:简单题型通关
1.不等式 x>x2 的解集是( )
A.{x|x>1} B.{x|x<0}
C.{x|0<x<1} D.R
x>x2
x2-x<0
x(x-1)<0
0C
课前预习
任务二:简单题型通关
2.不等式 x2+6x+10<0 的解集是( )
A. B.R
C.{x|x>5} D.{x|x<2}
A
Δ=62-4×10<0
x2+6x+10恒大于0
课前预习
任务二:简单题型通关
3.二次方程ax2+bx+c=0的两根为-2,3,a<0,那么ax2+bx+c>0的解集为( )
A.{x|x>3或x<-2} B.{x|x>2或x<-3}
C.{x|-2<x<3} D.{x|-3< x<2}
y=ax2+bx+c的图象开口向下
y>0取两根之间
C
课前预习
任务二:简单题型通关
4.不等式-x2+x-2<0的解集为________.
Δ=12-4×(-2)×(-1)=-7<0
不等式解集为R
R
新知精讲
1.一元二次不等式
新知精讲
2.一元二次不等式的解与解集
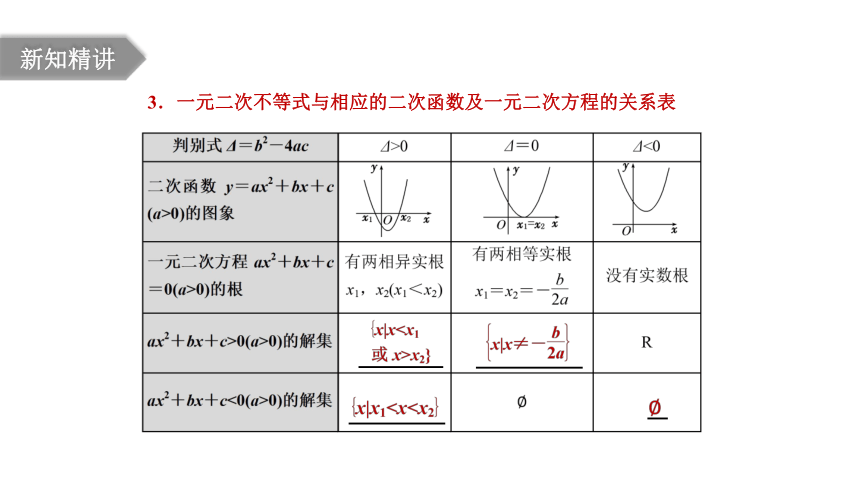
新知精讲
3.一元二次不等式与相应的二次函数及一元二次方程的关系表
题型探究
题型一 一元二次不等式的解法
例1 解下列不等式:
(1)2x2+5x-3<0; (2)-3x2+6x≤2;
(3)4x2+4x+1>0; (4)-x2+6x-10>0.
题型探究
题型一 一元二次不等式的解法
(1)2x2+5x-3<0
原不等式的解集为
Δ=49>0
2x2+5x-3=0的两根为x1=-3,x2=
y=2x2+5x-3的图象,如图①所示
题型探究
题型一 一元二次不等式的解法
(2)-3x2+6x≤2
原不等式的解集为
3x2-6x+2≥0
Δ=12>0
3x2-6x+2=0的解为x1= ,x2=
作出y=3x2-6x+2的图象,如图②所示
题型探究
题型一 一元二次不等式的解法
(3) 4x2+4x+1>0
Δ=0
方程4x2+4x+1=0有两个相等的实根x1=x2=
作出函数y=4x2+4x+1的图象如图所示
原不等式的解集为
题型探究
题型一 一元二次不等式的解法
(4)-x2+6x-10>0
原不等式的解集为
x2-6x+10<0
Δ=-4<0
方程x2-6x+10=0无实根
归纳总结
解一元二次不等式的一般步骤
(1)通过对不等式变形,使二次项系数大于零;
(2)计算对应方程的判别式;
(3)求出相应的一元二次方程的根,或根据判别式说明方程没有实根;
(4)根据函数图象与x轴的相关位置写出不等式的解集.
活学活用
1.已知集合M={x|x2-3x-28≤0},N={x|x2-x-6>0},则M∩N为( )
A.{x|-4≤x<-2或3<x≤7} B.{x|-4<x≤-2或3≤x<7}
C.{x|x≤-2或x>3} D.{x|x<-2或x≥3}
A
M={x|x2-3x-28≤0}={x|-4≤x≤7}
N={x|x2-x-6>0}={x|x<-2或x>3}
M∩N={x|-4≤x<-2或3<x≤7}
题型探究
题型二 三个“二次”关系的应用
例2 若不等式ax2+bx+2>0的解集是,则a+b的值为( )
A.14 B.-10
C.10 D.-14
ax2+bx+2=0的解为,,且a<0.
a+b=-14
D
题型探究
题型二 三个“二次”关系的应用
例3 已知一元二次不等式x2+px+q<0的解集为,求不等式qx2+px+1>0的解集.
x1=-与x2=是方程x2+px+q=0的两个实数根
qx2+px+1>0
- x2+ x+1>0
x2-x-6<0
-2<x<3
归纳总结
一元二次不等式ax2+bx+c>0(a≠0)的解集的端点值是一元二次方程ax2+bx+c=0的根,也是函数y=ax2+bx+c与x轴交点的横坐标.
二次函数y=ax2+bx+c的图象在x轴上方的部分,是由不等式ax2+bx+c>0的x的值构成的;图象在x轴下方的部分,是由不等式ax2+bx+c<0的x的值构成的.
活学活用
2.若不等式y=ax2-x-c>0的解集为(-2,1),则函数y的图象为( )
B
活学活用
3.已知不等式ax2+bx+c>0的解集为{x|20的解集.
cx2-bx+a>0
6ax2+5ax+a>0(a<0)
6x2+5x+1<0
题型探究
题型三 解含参数的一元二次不等式
例4 解关于x的不等式 x2+(1-a)x-a<0.
x2+(1-a)x-a=0的解为x1=-1,x2=a
函数y=x2+(1-a)x-a的图象开口向上
当a<-1时,原不等式解集为{x|a<x<-1}
当a=-1时,原不等式解集为
当a>-1时,原不等式解集为{x|-1<x<a}
分类讨论
归纳总结
解含参数的一元二次不等式时的注意点
(1)若二次项系数含有参数,则需对二次项系数大于0与小于0进行讨论;
(2)若求对应一元二次方程的根需用公式,则应对判别式Δ进行讨论;
(3)若求出的根中含有参数,则应对两根的大小进行讨论.
活学活用
4.设a∈R,解关于x的不等式ax2+(1-2a)x-2>0.
分类讨论
当a=0时
当a≠0时
ax2+(1-2a)x-2=0的两根分别为2和-
①当a<-时,原不等式解集为{x|-②当a=- 时,原不等式的解集为
③当-④当a>0时,原不等式的解集为
x-2>0
ax2+(1-2a)x-2>0
原不等式的解集为{x|x>2}
思想方法
分类讨论思想在解含参数不等式中的应用
例4 解关于x的不等式 ax2-(a-1)x-1<0(a∈R).
(ax+1)(x-1)<0
当a>0时
解集为{x| }
当a=0时
解集为
当-1解集为
当a=-1时
解集为
当a<-1时
解集为
感悟提高
分类讨论是解决含有参数的一元二次不等式的主要方法,确定分类讨论的标准时,要着重处理好以下三点:
(1)讨论的“时刻”,即在什么时候开始进行讨论.
(2)讨论的“点”,即以哪个量为标准进行讨论.
(3)考虑要周到,即讨论对象的各种情况都要加以分析,给出结论.
达标检测
1.已知不等式ax2-5x+b>0的解集为,则不等式bx2-5x+a>0的解集为( )
A. B.
C.{x|-32}
ax2-5x+b=0的解是x1=-,x2=
x1+x2=-+=
x1x2=- × =
a=30,b=-5
bx2-5x+a>0 -5x2-5x+30>0
-3C
达标检测
2.已知不等式 ax2+3x-2>0的解集为{x|1A.a=1,b=-2 B.a=2,b=-1
C.a=-1,b=2 D.a=-2,b=1
a<0,且方程ax2+3x-2=0的两个根分别为1和b
1+b=-,b=
a=-1,b=2
C
达标检测
3.二次函数y=x2-4x+3在 y<0 时x的取值范围是_____________.
x2-4x+3<0
1{x|1本课小结
1.一元二次不等式的有关概念
2.一元二次不等式的解法
3.一元二次不等式与相应的二次函数及一元二次方程的关系
2.2.3一元二次不等式的解法
高一
必修一
本节目标
1 .了解一元二次不等式的概念.
2.理解一元二次不等式、一元二次方程与二次函数的关系.
3.会解一元二次不等式.
情景引入
二次函数
与一元二次方程
不等式
任务一:知识预习
课前预习
预习课本,思考并完成以下问题
(1)怎样判断一个不等式是否为一元二次不等式?
(2)如何求解一元二次不等式?
(3)三个“二次”指的是哪三个“二次”?它们之间有何关系?
课前预习
任务二:简单题型通关
1.不等式 x>x2 的解集是( )
A.{x|x>1} B.{x|x<0}
C.{x|0<x<1} D.R
x>x2
x2-x<0
x(x-1)<0
0
课前预习
任务二:简单题型通关
2.不等式 x2+6x+10<0 的解集是( )
A. B.R
C.{x|x>5} D.{x|x<2}
A
Δ=62-4×10<0
x2+6x+10恒大于0
课前预习
任务二:简单题型通关
3.二次方程ax2+bx+c=0的两根为-2,3,a<0,那么ax2+bx+c>0的解集为( )
A.{x|x>3或x<-2} B.{x|x>2或x<-3}
C.{x|-2<x<3} D.{x|-3< x<2}
y=ax2+bx+c的图象开口向下
y>0取两根之间
C
课前预习
任务二:简单题型通关
4.不等式-x2+x-2<0的解集为________.
Δ=12-4×(-2)×(-1)=-7<0
不等式解集为R
R
新知精讲
1.一元二次不等式
新知精讲
2.一元二次不等式的解与解集
新知精讲
3.一元二次不等式与相应的二次函数及一元二次方程的关系表
题型探究
题型一 一元二次不等式的解法
例1 解下列不等式:
(1)2x2+5x-3<0; (2)-3x2+6x≤2;
(3)4x2+4x+1>0; (4)-x2+6x-10>0.
题型探究
题型一 一元二次不等式的解法
(1)2x2+5x-3<0
原不等式的解集为
Δ=49>0
2x2+5x-3=0的两根为x1=-3,x2=
y=2x2+5x-3的图象,如图①所示
题型探究
题型一 一元二次不等式的解法
(2)-3x2+6x≤2
原不等式的解集为
3x2-6x+2≥0
Δ=12>0
3x2-6x+2=0的解为x1= ,x2=
作出y=3x2-6x+2的图象,如图②所示
题型探究
题型一 一元二次不等式的解法
(3) 4x2+4x+1>0
Δ=0
方程4x2+4x+1=0有两个相等的实根x1=x2=
作出函数y=4x2+4x+1的图象如图所示
原不等式的解集为
题型探究
题型一 一元二次不等式的解法
(4)-x2+6x-10>0
原不等式的解集为
x2-6x+10<0
Δ=-4<0
方程x2-6x+10=0无实根
归纳总结
解一元二次不等式的一般步骤
(1)通过对不等式变形,使二次项系数大于零;
(2)计算对应方程的判别式;
(3)求出相应的一元二次方程的根,或根据判别式说明方程没有实根;
(4)根据函数图象与x轴的相关位置写出不等式的解集.
活学活用
1.已知集合M={x|x2-3x-28≤0},N={x|x2-x-6>0},则M∩N为( )
A.{x|-4≤x<-2或3<x≤7} B.{x|-4<x≤-2或3≤x<7}
C.{x|x≤-2或x>3} D.{x|x<-2或x≥3}
A
M={x|x2-3x-28≤0}={x|-4≤x≤7}
N={x|x2-x-6>0}={x|x<-2或x>3}
M∩N={x|-4≤x<-2或3<x≤7}
题型探究
题型二 三个“二次”关系的应用
例2 若不等式ax2+bx+2>0的解集是,则a+b的值为( )
A.14 B.-10
C.10 D.-14
ax2+bx+2=0的解为,,且a<0.
a+b=-14
D
题型探究
题型二 三个“二次”关系的应用
例3 已知一元二次不等式x2+px+q<0的解集为,求不等式qx2+px+1>0的解集.
x1=-与x2=是方程x2+px+q=0的两个实数根
qx2+px+1>0
- x2+ x+1>0
x2-x-6<0
-2<x<3
归纳总结
一元二次不等式ax2+bx+c>0(a≠0)的解集的端点值是一元二次方程ax2+bx+c=0的根,也是函数y=ax2+bx+c与x轴交点的横坐标.
二次函数y=ax2+bx+c的图象在x轴上方的部分,是由不等式ax2+bx+c>0的x的值构成的;图象在x轴下方的部分,是由不等式ax2+bx+c<0的x的值构成的.
活学活用
2.若不等式y=ax2-x-c>0的解集为(-2,1),则函数y的图象为( )
B
活学活用
3.已知不等式ax2+bx+c>0的解集为{x|2
cx2-bx+a>0
6ax2+5ax+a>0(a<0)
6x2+5x+1<0
题型探究
题型三 解含参数的一元二次不等式
例4 解关于x的不等式 x2+(1-a)x-a<0.
x2+(1-a)x-a=0的解为x1=-1,x2=a
函数y=x2+(1-a)x-a的图象开口向上
当a<-1时,原不等式解集为{x|a<x<-1}
当a=-1时,原不等式解集为
当a>-1时,原不等式解集为{x|-1<x<a}
分类讨论
归纳总结
解含参数的一元二次不等式时的注意点
(1)若二次项系数含有参数,则需对二次项系数大于0与小于0进行讨论;
(2)若求对应一元二次方程的根需用公式,则应对判别式Δ进行讨论;
(3)若求出的根中含有参数,则应对两根的大小进行讨论.
活学活用
4.设a∈R,解关于x的不等式ax2+(1-2a)x-2>0.
分类讨论
当a=0时
当a≠0时
ax2+(1-2a)x-2=0的两根分别为2和-
①当a<-时,原不等式解集为{x|-
③当-
x-2>0
ax2+(1-2a)x-2>0
原不等式的解集为{x|x>2}
思想方法
分类讨论思想在解含参数不等式中的应用
例4 解关于x的不等式 ax2-(a-1)x-1<0(a∈R).
(ax+1)(x-1)<0
当a>0时
解集为{x| }
当a=0时
解集为
当-1
当a=-1时
解集为
当a<-1时
解集为
感悟提高
分类讨论是解决含有参数的一元二次不等式的主要方法,确定分类讨论的标准时,要着重处理好以下三点:
(1)讨论的“时刻”,即在什么时候开始进行讨论.
(2)讨论的“点”,即以哪个量为标准进行讨论.
(3)考虑要周到,即讨论对象的各种情况都要加以分析,给出结论.
达标检测
1.已知不等式ax2-5x+b>0的解集为,则不等式bx2-5x+a>0的解集为( )
A. B.
C.{x|-3
ax2-5x+b=0的解是x1=-,x2=
x1+x2=-+=
x1x2=- × =
a=30,b=-5
bx2-5x+a>0 -5x2-5x+30>0
-3
达标检测
2.已知不等式 ax2+3x-2>0的解集为{x|1
C.a=-1,b=2 D.a=-2,b=1
a<0,且方程ax2+3x-2=0的两个根分别为1和b
1+b=-,b=
a=-1,b=2
C
达标检测
3.二次函数y=x2-4x+3在 y<0 时x的取值范围是_____________.
x2-4x+3<0
1
1.一元二次不等式的有关概念
2.一元二次不等式的解法
3.一元二次不等式与相应的二次函数及一元二次方程的关系
