人教B版(2019)数学必修第一册3.1.2 函数的最大(小)值 课件(共30张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册3.1.2 函数的最大(小)值 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 915.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 15:50:07 | ||
图片预览









文档简介
(共30张PPT)
3.1.2 函数的最大(小)值
高一
必修一
本节目标
1. 理解函数的最大值、最小值及其几何意义
2. 能求一些简单函数的最大值、最小值
任务一:知识预习
课前预习
(1)函数最大(小)值的定义是什么?
(2)从函数的图象可以看出函数最值的几何意义是什么?
预习课本,思考并完成以下问题
任务二:简单题型通关
课前预习
1.函数f(x)=在[1,+∞)上( )
A.有最大值无最小值 B.有最小值无最大值
C.有最大值也有最小值 D.无最大值也无最小值
A
任务二:简单题型通关
课前预习
0
0
-1
任务二:简单题型通关
课前预习
A
新知精讲
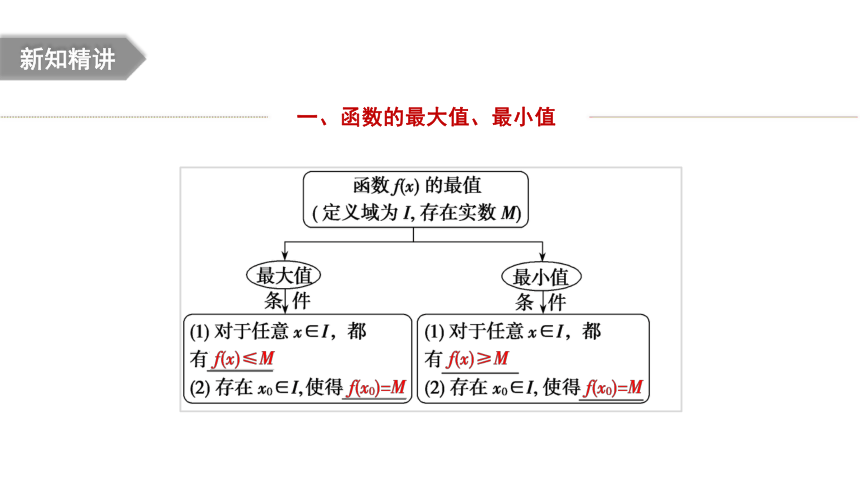
一、函数的最大值、最小值
1.函数y=f(x)的最大值是图象最高点的________坐标.
2.函数y=f(x)的最小值是图象最低点的________坐标.
新知精讲
二、函数最大值、最小值的几何意义
最大(小)值必须是一个函数值,是值域中的一个元素,如函数y=x2(x∈R)的最小值是0,有f(0)=0.
易错提示
题型探究
题型一 图象法求函数的最值
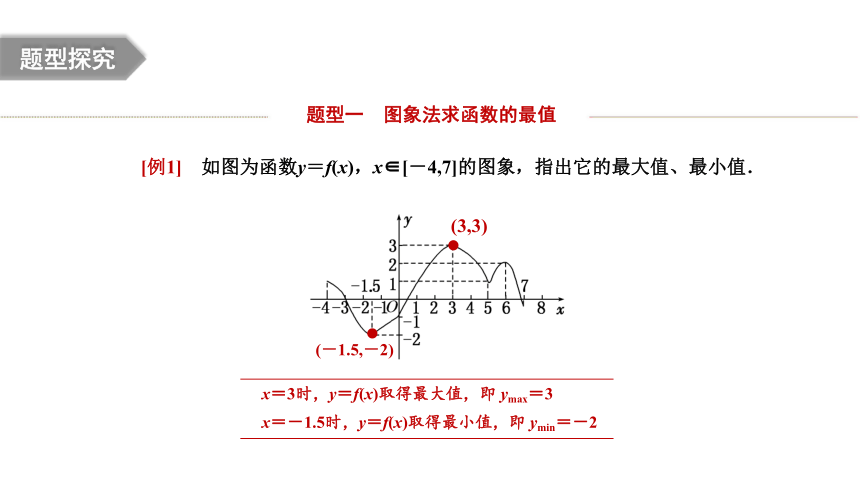
[例1] 如图为函数y=f(x),x∈[-4,7]的图象,指出它的最大值、最小值.
(3,3)
(-1.5,-2)
x=3时,y=f(x)取得最大值,即 ymax=3
x=-1.5时,y=f(x)取得最小值,即 ymin=-2
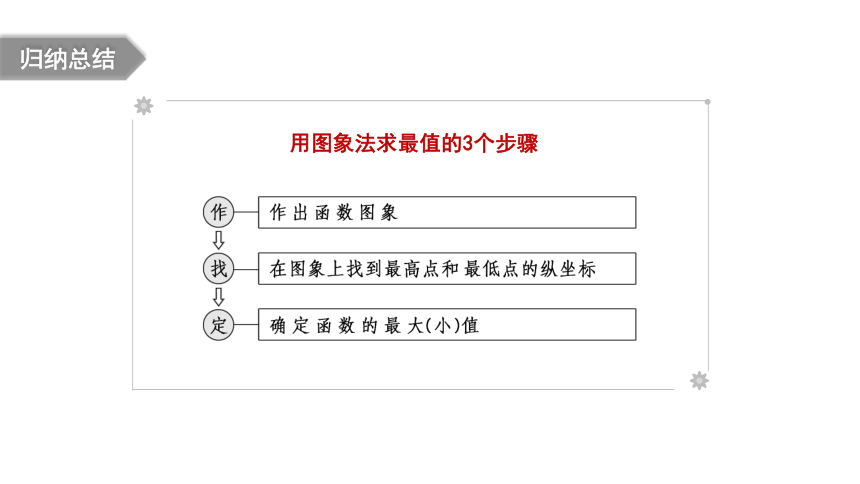
归纳总结
用图象法求最值的3个步骤
活学活用
由图象可知f(x)的最小值为f(1)=1,无最大值
题型探究
题型二
利用单调性求函数的最值
[例2] 已知函数f(x)=x+.
(1)证明:f(x)在(1,+∞)内是增函数;
(2)求f(x)在[2,4]上的最值.
题型探究
[例2] 已知函数f(x)=x+.
(1)证明:f(x)在(1,+∞)内是增函数;
x2>x1>1
x1-x2<0
x1x2>1
x1x2-1>0
f(x)在(1,+∞)内是增函数
f(x1)<f(x2)
题型探究
[例2] 已知函数f(x)=x+.
(2)求f(x)在[2,4]上的最值.
归纳总结
函数的最值与单调性的关系
(1)如果y=f(x)在 (a,b]上是增函数,在[b,c)上是减函数,则y=f(x),x∈(a,c)在x=b处有最大值f(b).
(2)如果y=f(x)在 (a,b]上是减函数,在 [b,c)上是增函数,则y=f(x),x∈(a,c)在x=b处有最小值f(b).
(3)如果y=f(x)在 [a,b]上是增(减)函数,则在区间[a,b]的左、右端点处分别取得最小(大)值、最大(小)值.
活学活用
设x1,x2是区间[2,6]上的任意两个实数,且x1f(x1)-f(x2)>0
f(x1)>f(x2)
函数f(x)=是区间[2,6]上的减函数
x=2时取最大值,最大值是2,x=6时取最小值,最小值是0.4
2≤x1x2-x1>0
(x1-1)(x2-1)>0
题型探究
题型三
实际应用中的最值
(1)将利润表示为月产量的函数f(x);
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本+利润)
题型探究
(1)将利润表示为月产量的函数f(x);
题型探究
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本+利润)
当0≤x≤400时, f(x)=-(x-300)2+25 000
当x=300时,[f(x)]max=25 000
当x>400时,f(x)=60 000-100x是减函数
f(x)<60 000-100×400<25 000
当x=300时,[f(x)]max=25 000
归纳总结
解实际应用问题的5个步骤
(1)审:审清题意,读懂题,找出各量之间的关系.
(2)设:从实际问题中抽象出数学模型,恰当设出未知数.
(3)列:根据已知条件列出正确的数量关系.
(4)解:转化为求函数的最值或解方程或解不等式.
(5)答:回归实际,明确答案,得出结论.
活学活用
3.将进货单价为40元的商品按50元一个出售时,能卖出500个,已知这种商品每涨价1元,其销售量就减少10个,为得到最大利润,售价应为多少元?最大利润为多少?
设售价为x元,利润为y元
y=(x-40)(1 000-10x)=-10(x-70)2+9 000≤9 000
单个涨价(x-50)元,销量减少10(x-50)个,销量为500-10(x-50)=(1 000-10x)个
x=70时,ymax=9 000
售价为70元时,利润最大值为9 000元
题型探究
[例4] 求二次函数 f(x)=x2-2ax+2 在[2,4]上的最小值.
函数图象的对称轴是x=a
当a<2时,f(x)在[2,4]上是增函数
f(x)min=f(2)=6-4a
当a>4时,f(x)在[2,4]上是减函数
f(x)min=f(4)=18-8a
当2≤a≤4时,f(x)min=f(a)=2-a2
分类讨论
一题多变
1.[变设问]在本例条件下,求f(x)的最大值.
[例4] 求二次函数 f(x)=x2-2ax+2 在[2,4]上的最小值.
函数图象的对称轴是x=a
当a≤3时,f(x)max=f(4)=18-8a
当a>3时,f(x)max=f(2)=6-4a
一题多变
2.[变设问]在本例条件下,若f(x)的最小值为2,求a的值.
[例4] 求二次函数 f(x)=x2-2ax+2 在[2,4]上的最小值.
一题多变
3.[变条件,变设问]本例条件变为,若f(x)=x2-2ax+2,当 x∈[2,4]时,f(x)≤a 恒成立,求实数a的取值范围.
[例4] 求二次函数 f(x)=x2-2ax+2 在[2,4]上的最小值.
a≥x2-2ax+2在[2,4]内恒成立
a≥f(x)max,x∈[2,4]
由本例探究1知f(x)max=
(1)当a≤3时,a≥18-8a,解得a≥2,此时有2≤a≤3
(2)当a>3时,a≥6-4a,解得a≥,此时有a>3.
综上有实数a的取值范围是[2,+∞)
归纳总结
求解二次函数最值问题的顺序
(1)确定对称轴与抛物线的开口方向、作图.
(2)在图象上标出定义域的位置.
(3)观察单调性写出最值.
达标检测
1.若函数y=x2+2x+2在闭区间 [m,1]上有最大值5,最小值1,则m的取值范围是( )
A.[-1,1] B.[-1,+∞) C.[-3,0] D.[-3,-1]
y=x2+2x+2=(x+1)2+1
要使函数值为5,需x=1或x=-3
图象开口向上,对称轴是x=-1,最小值为1
m的取值范围是[-3,-1].
D
达标检测
2.某公司在甲、乙两地同时销售一种品牌车,利润(单位:万元)分别为L1=-x2+21x和L2=2x,其中销售量单位:辆.若该公司在两地共销售15辆,则能获得的最大利润为( )
A.90万元 B.60万元 C.120万元 D.120.25万元
设公司在甲地销售x辆,则在乙地销售15-x辆
公司获利为
当x=9或10时,L最大为120万元
C
达标检测
对称轴为直线x=
<0,即a<0时,[0,1]是f(x)的递减区间
f(x)max=f(0)=-4a-a2=-5
a=1(舍),或a=-5
当>1,即a>2时, [0,1]是f(x)的递增区间
f(x)max=f(1)=-4-a2=-5
a=1 (舍) ,或a=-1 (舍)
当0≤ ≤1,即0≤a≤2时
f(x)max=f()=-4a=-5
a=
a=-5,或a=
3.已知 f(x)=-4x2+4ax-4a-a2 在区间[0,1]内有最大值-5,求a的值.
本课小结
1. 函数最大(小)值的定义是什么?
2. 函数最值的几何意义是什么?
3. 函数的最值与单调性的关系。
3.1.2 函数的最大(小)值
高一
必修一
本节目标
1. 理解函数的最大值、最小值及其几何意义
2. 能求一些简单函数的最大值、最小值
任务一:知识预习
课前预习
(1)函数最大(小)值的定义是什么?
(2)从函数的图象可以看出函数最值的几何意义是什么?
预习课本,思考并完成以下问题
任务二:简单题型通关
课前预习
1.函数f(x)=在[1,+∞)上( )
A.有最大值无最小值 B.有最小值无最大值
C.有最大值也有最小值 D.无最大值也无最小值
A
任务二:简单题型通关
课前预习
0
0
-1
任务二:简单题型通关
课前预习
A
新知精讲
一、函数的最大值、最小值
1.函数y=f(x)的最大值是图象最高点的________坐标.
2.函数y=f(x)的最小值是图象最低点的________坐标.
新知精讲
二、函数最大值、最小值的几何意义
最大(小)值必须是一个函数值,是值域中的一个元素,如函数y=x2(x∈R)的最小值是0,有f(0)=0.
易错提示
题型探究
题型一 图象法求函数的最值
[例1] 如图为函数y=f(x),x∈[-4,7]的图象,指出它的最大值、最小值.
(3,3)
(-1.5,-2)
x=3时,y=f(x)取得最大值,即 ymax=3
x=-1.5时,y=f(x)取得最小值,即 ymin=-2
归纳总结
用图象法求最值的3个步骤
活学活用
由图象可知f(x)的最小值为f(1)=1,无最大值
题型探究
题型二
利用单调性求函数的最值
[例2] 已知函数f(x)=x+.
(1)证明:f(x)在(1,+∞)内是增函数;
(2)求f(x)在[2,4]上的最值.
题型探究
[例2] 已知函数f(x)=x+.
(1)证明:f(x)在(1,+∞)内是增函数;
x2>x1>1
x1-x2<0
x1x2>1
x1x2-1>0
f(x)在(1,+∞)内是增函数
f(x1)<f(x2)
题型探究
[例2] 已知函数f(x)=x+.
(2)求f(x)在[2,4]上的最值.
归纳总结
函数的最值与单调性的关系
(1)如果y=f(x)在 (a,b]上是增函数,在[b,c)上是减函数,则y=f(x),x∈(a,c)在x=b处有最大值f(b).
(2)如果y=f(x)在 (a,b]上是减函数,在 [b,c)上是增函数,则y=f(x),x∈(a,c)在x=b处有最小值f(b).
(3)如果y=f(x)在 [a,b]上是增(减)函数,则在区间[a,b]的左、右端点处分别取得最小(大)值、最大(小)值.
活学活用
设x1,x2是区间[2,6]上的任意两个实数,且x1
f(x1)>f(x2)
函数f(x)=是区间[2,6]上的减函数
x=2时取最大值,最大值是2,x=6时取最小值,最小值是0.4
2≤x1
(x1-1)(x2-1)>0
题型探究
题型三
实际应用中的最值
(1)将利润表示为月产量的函数f(x);
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本+利润)
题型探究
(1)将利润表示为月产量的函数f(x);
题型探究
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本+利润)
当0≤x≤400时, f(x)=-(x-300)2+25 000
当x=300时,[f(x)]max=25 000
当x>400时,f(x)=60 000-100x是减函数
f(x)<60 000-100×400<25 000
当x=300时,[f(x)]max=25 000
归纳总结
解实际应用问题的5个步骤
(1)审:审清题意,读懂题,找出各量之间的关系.
(2)设:从实际问题中抽象出数学模型,恰当设出未知数.
(3)列:根据已知条件列出正确的数量关系.
(4)解:转化为求函数的最值或解方程或解不等式.
(5)答:回归实际,明确答案,得出结论.
活学活用
3.将进货单价为40元的商品按50元一个出售时,能卖出500个,已知这种商品每涨价1元,其销售量就减少10个,为得到最大利润,售价应为多少元?最大利润为多少?
设售价为x元,利润为y元
y=(x-40)(1 000-10x)=-10(x-70)2+9 000≤9 000
单个涨价(x-50)元,销量减少10(x-50)个,销量为500-10(x-50)=(1 000-10x)个
x=70时,ymax=9 000
售价为70元时,利润最大值为9 000元
题型探究
[例4] 求二次函数 f(x)=x2-2ax+2 在[2,4]上的最小值.
函数图象的对称轴是x=a
当a<2时,f(x)在[2,4]上是增函数
f(x)min=f(2)=6-4a
当a>4时,f(x)在[2,4]上是减函数
f(x)min=f(4)=18-8a
当2≤a≤4时,f(x)min=f(a)=2-a2
分类讨论
一题多变
1.[变设问]在本例条件下,求f(x)的最大值.
[例4] 求二次函数 f(x)=x2-2ax+2 在[2,4]上的最小值.
函数图象的对称轴是x=a
当a≤3时,f(x)max=f(4)=18-8a
当a>3时,f(x)max=f(2)=6-4a
一题多变
2.[变设问]在本例条件下,若f(x)的最小值为2,求a的值.
[例4] 求二次函数 f(x)=x2-2ax+2 在[2,4]上的最小值.
一题多变
3.[变条件,变设问]本例条件变为,若f(x)=x2-2ax+2,当 x∈[2,4]时,f(x)≤a 恒成立,求实数a的取值范围.
[例4] 求二次函数 f(x)=x2-2ax+2 在[2,4]上的最小值.
a≥x2-2ax+2在[2,4]内恒成立
a≥f(x)max,x∈[2,4]
由本例探究1知f(x)max=
(1)当a≤3时,a≥18-8a,解得a≥2,此时有2≤a≤3
(2)当a>3时,a≥6-4a,解得a≥,此时有a>3.
综上有实数a的取值范围是[2,+∞)
归纳总结
求解二次函数最值问题的顺序
(1)确定对称轴与抛物线的开口方向、作图.
(2)在图象上标出定义域的位置.
(3)观察单调性写出最值.
达标检测
1.若函数y=x2+2x+2在闭区间 [m,1]上有最大值5,最小值1,则m的取值范围是( )
A.[-1,1] B.[-1,+∞) C.[-3,0] D.[-3,-1]
y=x2+2x+2=(x+1)2+1
要使函数值为5,需x=1或x=-3
图象开口向上,对称轴是x=-1,最小值为1
m的取值范围是[-3,-1].
D
达标检测
2.某公司在甲、乙两地同时销售一种品牌车,利润(单位:万元)分别为L1=-x2+21x和L2=2x,其中销售量单位:辆.若该公司在两地共销售15辆,则能获得的最大利润为( )
A.90万元 B.60万元 C.120万元 D.120.25万元
设公司在甲地销售x辆,则在乙地销售15-x辆
公司获利为
当x=9或10时,L最大为120万元
C
达标检测
对称轴为直线x=
<0,即a<0时,[0,1]是f(x)的递减区间
f(x)max=f(0)=-4a-a2=-5
a=1(舍),或a=-5
当>1,即a>2时, [0,1]是f(x)的递增区间
f(x)max=f(1)=-4-a2=-5
a=1 (舍) ,或a=-1 (舍)
当0≤ ≤1,即0≤a≤2时
f(x)max=f()=-4a=-5
a=
a=-5,或a=
3.已知 f(x)=-4x2+4ax-4a-a2 在区间[0,1]内有最大值-5,求a的值.
本课小结
1. 函数最大(小)值的定义是什么?
2. 函数最值的几何意义是什么?
3. 函数的最值与单调性的关系。
