人教B版(2019)数学必修第一册3.1.1 函数的表示法 课件(共34张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册3.1.1 函数的表示法 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 16:10:10 | ||
图片预览









文档简介
(共34张PPT)
3.1.1 函数的表示法
高一
必修一
本节目标
1. 掌握函数的三种表示方法.
2.会识别简单的图象.
任务一 知识预习
课前预习
(1)表示两个变量之间函数关系的方法有几种?分别是什么?
(2)函数的各种表示法各有什么特点?
预习课本,思考并完成以下问题
课前预习
任务二 简单题型通关
D
课前预习
任务二 简单题型通关
2.下列函数中,不满足f(2x)=2f(x)的是( )
A.f(x)=|x| B.f(x)=x-|x|
C.f(x)=x+1 D.f(x)=-x
C
课前预习
任务二 简单题型通关
3.函数f(x)=|x-1|的图象为( )
B
课前预习
任务二 简单题型通关
4.若 f(x)=x2,则 f(2x-1)=_____________.
4x2-4x+1
f(2x-1)= (2x-1)2
新知精讲
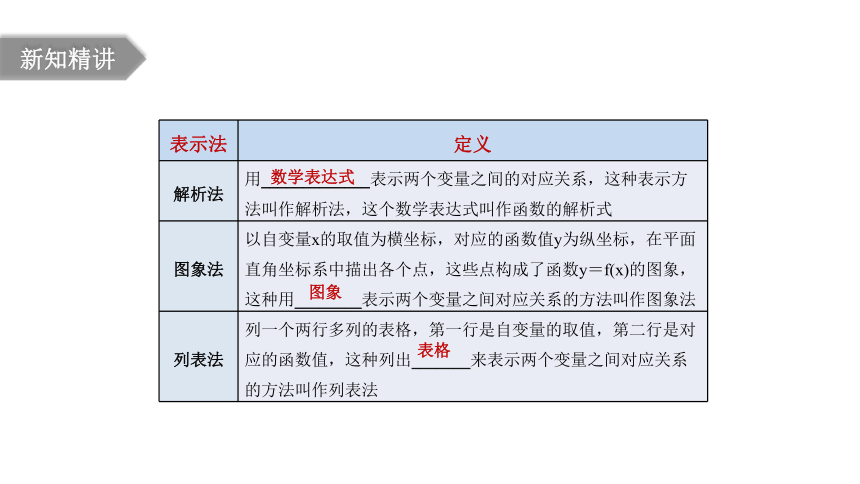
表示法 定义
解析法 用_____________表示两个变量之间的对应关系,这种表示方法叫作解析法,这个数学表达式叫作函数的解析式
图象法 以自变量x的取值为横坐标,对应的函数值y为纵坐标,在平面直角坐标系中描出各个点,这些点构成了函数y=f(x)的图象,这种用________表示两个变量之间对应关系的方法叫作图象法
列表法 列一个两行多列的表格,第一行是自变量的取值,第二行是对应的函数值,这种列出_______来表示两个变量之间对应关系的方法叫作列表法
数学表达式
图象
表格
新知精讲
小结
列表法、图象法和解析法是从三个不同的角度刻画自变量与函数值的对应关系,同一个函数可以用不同的方法表示.
题型探究
题型一 函数的表示法
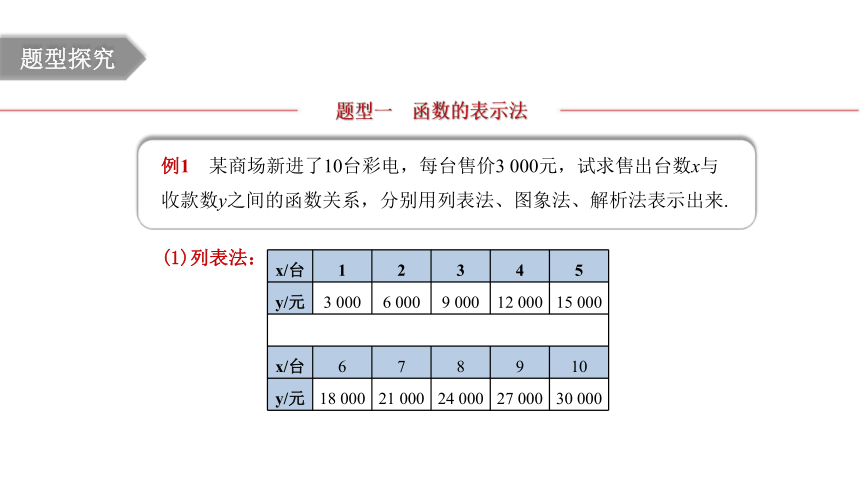
例1 某商场新进了10台彩电,每台售价3 000元,试求售出台数x与收款数y之间的函数关系,分别用列表法、图象法、解析法表示出来.
(1)列表法:
x/台 1 2 3 4 5
y/元 3 000 6 000 9 000 12 000 15 000
x/台 6 7 8 9 10
y/元 18 000 21 000 24 000 27 000 30 000
题型探究
题型一 函数的表示法
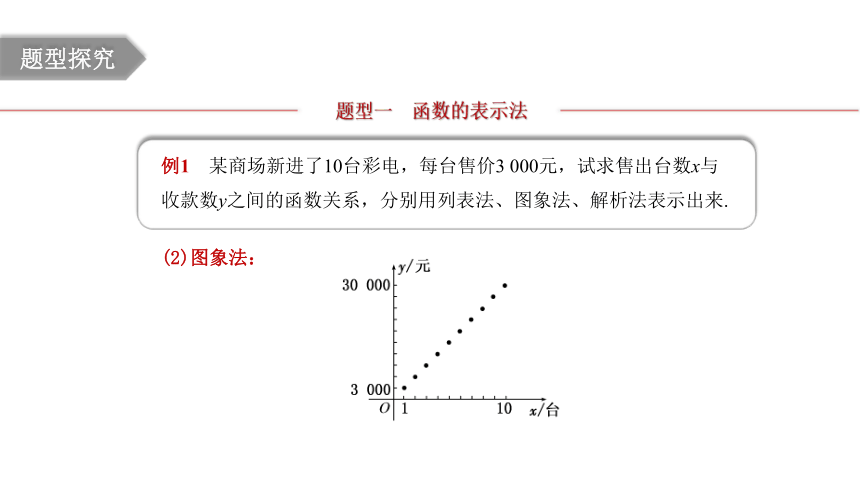
例1 某商场新进了10台彩电,每台售价3 000元,试求售出台数x与收款数y之间的函数关系,分别用列表法、图象法、解析法表示出来.
(2)图象法:
题型探究
题型一 函数的表示法
例1 某商场新进了10台彩电,每台售价3 000元,试求售出台数x与收款数y之间的函数关系,分别用列表法、图象法、解析法表示出来.
(3)解析法:
y=3 000x,x∈{1,2,3,…,10}
类题通法
理解函数的表示法3个关注点
(1)列表法、图象法、解析法均是函数的表示法,无论用哪种方式表示函数,都必须满足函数的概念.
(2)判断所给图象、表格、解析式是否表示函数的关键在于是否满足函数的定义.
(3)函数的三种表示法互相兼容或补充,许多函数是可以用三种方法表示的,但在实际操作中,仍以解析法为主.
活学活用
1.已知函数f(x),g(x)分别由下表给出.
x 1 2 3
f(x) 2 1 1
x 1 2 3
g(x) 3 2 1
则f ( g(1))的值为________;当g ( f (x))=2时,x=________.
g (1)=3
f ( g(1))=f (3)=1
1
g (2)=2
f (x)=2
x=1
1
题型探究
题型二 函数图象的作法及应用
例2 作出下列函数的图象并求出其值域.
(1)y=2x+1,x∈[0,2];
(2)y=,x∈[2,+∞);
(3)y=x2+2x,x∈[-2,2].
题型探究
题型二 函数图象的作法及应用
例2 作出下列函数的图象并求出其值域.
(1)y=2x+1,x∈[0,2];
观察图象可知,其值域为[1,5]
题型探究
题型二 函数图象的作法及应用
例2 作出下列函数的图象并求出其值域.
(2)y=,x∈[2,+∞);
观察图象可知其值域为(0,1]
题型探究
题型二 函数图象的作法及应用
例2 作出下列函数的图象并求出其值域.
(3)y=x2+2x,x∈[-2,2].
由图可得函数的值域是[-1,8]
类题通法
作函数y=f(x)图象的方法
(1)若y=f(x)是已学过的基本初等函数,则描出图象上的几个关键点,直接画出图象即可,有些可能需要根据定义域进行取舍.
(2)若y=f(x)不是所学过的基本初等函数之一,则要按:①列表;②描点;③连线 三个基本步骤作出y=f(x)的图象.
活学活用
2.作出下列函数的图象:
(1)y=1-x(x∈Z); (2)y=x2-4x+3,x∈[1,3].
图象如图①所示
易错提示:x∈Z,所以图象为直线y=1-x上的孤立点
y=x2-4x+3=(x-2)2-1
图象如图②所示
题型探究
题型三 函数解析式的求法
例3 求下列函数的解析式:
(1)已知函数 f (+1)=x+2,求f (x);
(2)已知函数f (x)是二次函数,且f (0)=1,f (x+1)-f (x)=2x,求f (x).
题型探究
题型三 函数解析式的求法
例3 求下列函数的解析式:
(1)已知函数f (+1)=x+2,求f (x)
换元法
法一
设t=+1
x=(t-1)2(t≥1)
f (t)=(t-1)2+2(t-1)=t2-2t+1+2t-2=t2-1
f (x)=x2-1(x≥1)
题型探究
题型三 函数解析式的求法
例3 求下列函数的解析式:
(1)已知函数f (+1)=x+2,求f (x)
配凑法
法二
x+2=()2+2+1-1=(+1)2-1
f (+1)=(+1)2-1(+1≥1)
f (x)=x2-1(x≥1)
题型探究
题型三 函数解析式的求法
例3 求下列函数的解析式:
(2)已知函数f (x)是二次函数,且f (0)=1,f (x+1)-f (x)=2x,求f (x).
设f (x)=ax2+bx+c(a≠0)
f (0)=1
c=1
f (x+1)-f (x)=2x
a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x
2ax+(a+b)=2x
f(x)=x2-x+1
类题通法
求函数解析式的4种常用求法
(1)配凑法:由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),便得f(x)的表达式;
(2)待定系数法:若已知函数的类型(如一次函数、二次函数)可用待定系数法;
(3)换元法:已知复合函数f(g(x))的解析式,可用换元法,此时要注意新元的取值范围;
(4)解方程组法:已知关于f(x)与f或f(-x)的表达式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出f(x).
活学活用
3.已知f (x+1)=x2-3x+2,求f (x).
法一
配凑法
f (x+1)=x2-3x+2=(x+1)2-5x+1=(x+1)2-5(x+1)+6
f (x)=x2-5x+6
活学活用
3.已知f (x+1)=x2-3x+2,求f (x).
法二
换元法
令t=x+1
x=t-1
f (t)=(t-1)2-3(t-1)+2=t2-5t+6
f (x)=x2-5x+6
活学活用
4.已知函数f(x)是一次函数,若f ( f (x))=4x+8,求f (x)的解析式.
f ( f (x))=4x+8
a2x+ab+b=4x+8
设f (x)=ax+b(a≠0)
f ( f (x))=f ( ax+b)=a(ax+b)+b=a2x+ab+b
或
f (x)=2x+或f (x)=-2x-8
活学活用
5.已知f (x)+2f (-x)=x2+2x,求f (x).
f (x)+2 f (-x)=x2+2x, ①
将x换成-x,得f (-x)+2 f (x)=x2-2x. ②
3 f (x)=x2-6x
f (x)=x2-2x
达标检测
1.已知f(x)是一次函数,2f(2)-3f(1)=5, 2f(0)-f(-1)=1,则f(x)=( )
A.3x+2 B.3x-2 C.2x+3 D.2x-3
设f(x)=kx+b(k≠0)
2f(2)-3f(1)=5,2f(0)-f(-1)=1
f(x)=3x-2
B
达标检测
令1-2x=t
x=(t≠1)
f(t)=-1
f()=16-1=15
C
法一
法二
令1-2x=
x=
f () =f(1-2×)==15
达标检测
C
(x+3x)·y=100
xy=50
达标检测
4.设二次函数f(x)满足f(2+x)=f(2-x),对于x∈R恒成立,且f(x)=0的两个实数根的平方和为10,f(x)的图象过点(0,3),求f(x)的解析式.
f(0)=3
k=3-4a
f(x)=a(x-2)2+3-4a=ax2-4ax+3
f(2+x)=f(2-x)
f(x)的图象关于直线x=2对称
设f(x)=a(x-2)2+k(a≠0)
10=+=(x1+x2)2-2x1x2=16-
a=1
f(x)=x2-4x+3
本课小结
3.1.1 函数的表示法
高一
必修一
本节目标
1. 掌握函数的三种表示方法.
2.会识别简单的图象.
任务一 知识预习
课前预习
(1)表示两个变量之间函数关系的方法有几种?分别是什么?
(2)函数的各种表示法各有什么特点?
预习课本,思考并完成以下问题
课前预习
任务二 简单题型通关
D
课前预习
任务二 简单题型通关
2.下列函数中,不满足f(2x)=2f(x)的是( )
A.f(x)=|x| B.f(x)=x-|x|
C.f(x)=x+1 D.f(x)=-x
C
课前预习
任务二 简单题型通关
3.函数f(x)=|x-1|的图象为( )
B
课前预习
任务二 简单题型通关
4.若 f(x)=x2,则 f(2x-1)=_____________.
4x2-4x+1
f(2x-1)= (2x-1)2
新知精讲
表示法 定义
解析法 用_____________表示两个变量之间的对应关系,这种表示方法叫作解析法,这个数学表达式叫作函数的解析式
图象法 以自变量x的取值为横坐标,对应的函数值y为纵坐标,在平面直角坐标系中描出各个点,这些点构成了函数y=f(x)的图象,这种用________表示两个变量之间对应关系的方法叫作图象法
列表法 列一个两行多列的表格,第一行是自变量的取值,第二行是对应的函数值,这种列出_______来表示两个变量之间对应关系的方法叫作列表法
数学表达式
图象
表格
新知精讲
小结
列表法、图象法和解析法是从三个不同的角度刻画自变量与函数值的对应关系,同一个函数可以用不同的方法表示.
题型探究
题型一 函数的表示法
例1 某商场新进了10台彩电,每台售价3 000元,试求售出台数x与收款数y之间的函数关系,分别用列表法、图象法、解析法表示出来.
(1)列表法:
x/台 1 2 3 4 5
y/元 3 000 6 000 9 000 12 000 15 000
x/台 6 7 8 9 10
y/元 18 000 21 000 24 000 27 000 30 000
题型探究
题型一 函数的表示法
例1 某商场新进了10台彩电,每台售价3 000元,试求售出台数x与收款数y之间的函数关系,分别用列表法、图象法、解析法表示出来.
(2)图象法:
题型探究
题型一 函数的表示法
例1 某商场新进了10台彩电,每台售价3 000元,试求售出台数x与收款数y之间的函数关系,分别用列表法、图象法、解析法表示出来.
(3)解析法:
y=3 000x,x∈{1,2,3,…,10}
类题通法
理解函数的表示法3个关注点
(1)列表法、图象法、解析法均是函数的表示法,无论用哪种方式表示函数,都必须满足函数的概念.
(2)判断所给图象、表格、解析式是否表示函数的关键在于是否满足函数的定义.
(3)函数的三种表示法互相兼容或补充,许多函数是可以用三种方法表示的,但在实际操作中,仍以解析法为主.
活学活用
1.已知函数f(x),g(x)分别由下表给出.
x 1 2 3
f(x) 2 1 1
x 1 2 3
g(x) 3 2 1
则f ( g(1))的值为________;当g ( f (x))=2时,x=________.
g (1)=3
f ( g(1))=f (3)=1
1
g (2)=2
f (x)=2
x=1
1
题型探究
题型二 函数图象的作法及应用
例2 作出下列函数的图象并求出其值域.
(1)y=2x+1,x∈[0,2];
(2)y=,x∈[2,+∞);
(3)y=x2+2x,x∈[-2,2].
题型探究
题型二 函数图象的作法及应用
例2 作出下列函数的图象并求出其值域.
(1)y=2x+1,x∈[0,2];
观察图象可知,其值域为[1,5]
题型探究
题型二 函数图象的作法及应用
例2 作出下列函数的图象并求出其值域.
(2)y=,x∈[2,+∞);
观察图象可知其值域为(0,1]
题型探究
题型二 函数图象的作法及应用
例2 作出下列函数的图象并求出其值域.
(3)y=x2+2x,x∈[-2,2].
由图可得函数的值域是[-1,8]
类题通法
作函数y=f(x)图象的方法
(1)若y=f(x)是已学过的基本初等函数,则描出图象上的几个关键点,直接画出图象即可,有些可能需要根据定义域进行取舍.
(2)若y=f(x)不是所学过的基本初等函数之一,则要按:①列表;②描点;③连线 三个基本步骤作出y=f(x)的图象.
活学活用
2.作出下列函数的图象:
(1)y=1-x(x∈Z); (2)y=x2-4x+3,x∈[1,3].
图象如图①所示
易错提示:x∈Z,所以图象为直线y=1-x上的孤立点
y=x2-4x+3=(x-2)2-1
图象如图②所示
题型探究
题型三 函数解析式的求法
例3 求下列函数的解析式:
(1)已知函数 f (+1)=x+2,求f (x);
(2)已知函数f (x)是二次函数,且f (0)=1,f (x+1)-f (x)=2x,求f (x).
题型探究
题型三 函数解析式的求法
例3 求下列函数的解析式:
(1)已知函数f (+1)=x+2,求f (x)
换元法
法一
设t=+1
x=(t-1)2(t≥1)
f (t)=(t-1)2+2(t-1)=t2-2t+1+2t-2=t2-1
f (x)=x2-1(x≥1)
题型探究
题型三 函数解析式的求法
例3 求下列函数的解析式:
(1)已知函数f (+1)=x+2,求f (x)
配凑法
法二
x+2=()2+2+1-1=(+1)2-1
f (+1)=(+1)2-1(+1≥1)
f (x)=x2-1(x≥1)
题型探究
题型三 函数解析式的求法
例3 求下列函数的解析式:
(2)已知函数f (x)是二次函数,且f (0)=1,f (x+1)-f (x)=2x,求f (x).
设f (x)=ax2+bx+c(a≠0)
f (0)=1
c=1
f (x+1)-f (x)=2x
a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x
2ax+(a+b)=2x
f(x)=x2-x+1
类题通法
求函数解析式的4种常用求法
(1)配凑法:由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),便得f(x)的表达式;
(2)待定系数法:若已知函数的类型(如一次函数、二次函数)可用待定系数法;
(3)换元法:已知复合函数f(g(x))的解析式,可用换元法,此时要注意新元的取值范围;
(4)解方程组法:已知关于f(x)与f或f(-x)的表达式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出f(x).
活学活用
3.已知f (x+1)=x2-3x+2,求f (x).
法一
配凑法
f (x+1)=x2-3x+2=(x+1)2-5x+1=(x+1)2-5(x+1)+6
f (x)=x2-5x+6
活学活用
3.已知f (x+1)=x2-3x+2,求f (x).
法二
换元法
令t=x+1
x=t-1
f (t)=(t-1)2-3(t-1)+2=t2-5t+6
f (x)=x2-5x+6
活学活用
4.已知函数f(x)是一次函数,若f ( f (x))=4x+8,求f (x)的解析式.
f ( f (x))=4x+8
a2x+ab+b=4x+8
设f (x)=ax+b(a≠0)
f ( f (x))=f ( ax+b)=a(ax+b)+b=a2x+ab+b
或
f (x)=2x+或f (x)=-2x-8
活学活用
5.已知f (x)+2f (-x)=x2+2x,求f (x).
f (x)+2 f (-x)=x2+2x, ①
将x换成-x,得f (-x)+2 f (x)=x2-2x. ②
3 f (x)=x2-6x
f (x)=x2-2x
达标检测
1.已知f(x)是一次函数,2f(2)-3f(1)=5, 2f(0)-f(-1)=1,则f(x)=( )
A.3x+2 B.3x-2 C.2x+3 D.2x-3
设f(x)=kx+b(k≠0)
2f(2)-3f(1)=5,2f(0)-f(-1)=1
f(x)=3x-2
B
达标检测
令1-2x=t
x=(t≠1)
f(t)=-1
f()=16-1=15
C
法一
法二
令1-2x=
x=
f () =f(1-2×)==15
达标检测
C
(x+3x)·y=100
xy=50
达标检测
4.设二次函数f(x)满足f(2+x)=f(2-x),对于x∈R恒成立,且f(x)=0的两个实数根的平方和为10,f(x)的图象过点(0,3),求f(x)的解析式.
f(0)=3
k=3-4a
f(x)=a(x-2)2+3-4a=ax2-4ax+3
f(2+x)=f(2-x)
f(x)的图象关于直线x=2对称
设f(x)=a(x-2)2+k(a≠0)
10=+=(x1+x2)2-2x1x2=16-
a=1
f(x)=x2-4x+3
本课小结
