人教B版(2019)数学必修第一册3.1.1 分段函数 课件(共29张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册3.1.1 分段函数 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 25.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 16:11:10 | ||
图片预览








文档简介
(共29张PPT)
3.1.1 分段函数
高一
必修一
情景引入
某公共汽车的票价如下:(1)5公里以内(含5公里)票价2元;(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算)。如果一条线路的总长为30公里。
请回答下列问题:
1.我如果坐车到离起点15公里的地方,票价为多少元?如果坐车到离起点18公里的地方呢?
2.写出票价与里程之间的函数关系式,并画出函数图象。
本节目标
1. 了解简单的分段函数,会求分段函数的值.
2.会画简单的分段函数图象,会应用函数图象解决简单的问题.
任务一:知识预习
课前预习
(1)什么是分段函数?分段函数是一个还是几个函数?
(2)怎样求分段函数的值?如何画分段函数的图象?
预习课本,思考并完成以下问题
任务二:简单题型通关
课前预习
B
任务二:简单题型通关
课前预习
[1,+∞)
任务二:简单题型通关
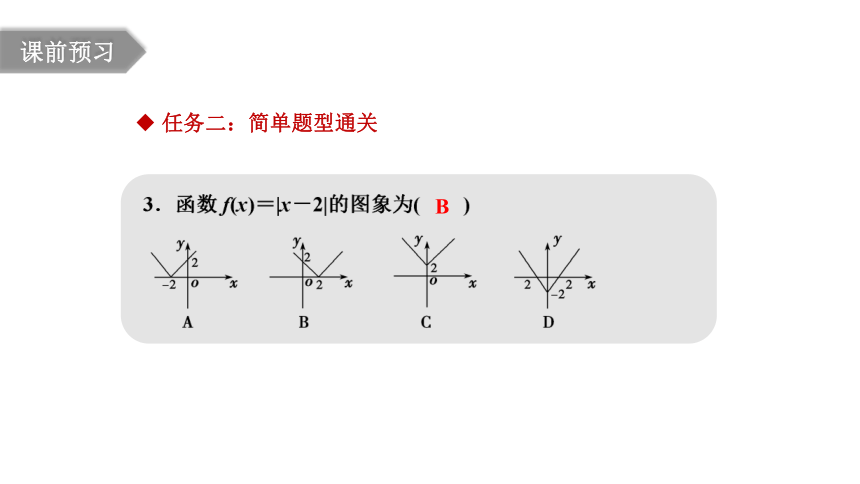
课前预习
B
任务二:简单题型通关
课前预习
D
新知精讲
分段函数
新知精讲
知识点睛
题型探究
题型探究
题型探究
分类讨论
若|x|≤1,则|x-1|-2=
若|x|>1,则
所以x的值为
x=或x=
因为|x|≤1,所以x的值不存在
x=,符合|x|>1
归纳总结
类题通法
1.求分段
函数函数值的方法
2.求某条件下自变量的值的方法
(1)确定要求值的自变量属于哪一段区间.
(2)代入该段的解析式求值,当出现 f(f(x0))的形式时,应从内到外依次求值.
先假设所求的值在分段函数定义区间的各段上,然后相应求出自变量的值,切记代入检验.
活学活用
分类讨论
当0<a<1时
f(a)=f(a+1)
=2a
当a≥1时
2(a-1)=2a,无解
综上,f =6
C
f(a)=
a+1>1
f(a+1)=2(a+1-1)=2a
a=或a=0(舍去)
f=f(4)=2×(4-1)=6
f(a)=2(a-1)
a+1≥2
f(a+1)=2(a+1-1)=2a
活学活用
综上可知,x0= 或x0=10
当x0≤2时
f(x0)=+2=8,即=6
x0=或x0=(舍去)
当x0>2时
f(x0)=x0
x0=10
或10
题型探究
题点一:分段函数图象的作法
归纳总结
分段函数图象的画法
作分段函数的图象时,分别作出各段的图象,在作每一段图象时,先不管定义域的限制,作出其图象,再保留定义域内的一段图象即可,作图时要特别注意接点处点的虚实,保证不重不漏.
题型探究
题点二:由函数图象确定其解析式
当-1≤x<0时
当0≤x≤1时
设f(x)=ax+b
将(-1,0),(0,1)代入
设f(x)=kx
将(1,-1)代入,则k=-1
题型探究
[例4] 已知f(x)=|x-1|+|x+1|.
(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;
(3)写出该函数的值域.
题型探究
[例4] 已知f(x)=|x-1|+|x+1|.
(1)用分段函数的形式表示该函数;
当x≥1时
|x-1|=x-1
|x+1|=x+1
f(x)=(x-1)+(x+1)=2x
当-1<x<1时
|x-1|=1-x
|x+1|=x+1
f(x)=(1-x)+(x+1)=2
当x≤-1时
|x-1|=1-x
|x+1|=-x-1
f(x)=(1-x)+(-x-1)=-2x
题型探究
[例4] 已知f(x)=|x-1|+|x+1|.
(2)画出该函数的图象; (3)写出该函数的值域.
(2)图象如图:
(3)由函数图象可以得知函数的值域为[2,+∞).
归纳总结
对含有绝对值的函数,要作其图象,首先应根据绝对值的意义去掉绝对值符号,将函数转化为分段函数,然后分段作出函数图象.
类题通法
活学活用
画出函数f(x)的图象得值域是(-∞,1]
(-∞,1]
达标检测
D
达标检测
B
1<<6
f()=
达标检测
① √ 符合函数定义,且在定义域的不同区间,有不同的对应关系.
② × 当x=2时,f(2)=3或4,故不是函数.
③ × 当x=1时,f(1)=5或1,故不是函数.
④ √ 符合函数定义,且在定义域的不同区间,有不同的对应关系.
B
达标检测
A.-3 B.-1 C.1 D.3
f(1)=2
f(a)+f(1)=0
f(a)=-2
A
a肯定小于0
f(a)=a+1=-2
a=-3
本课小结
1. 求分段函数的函数值的方法
2. 求某条件下自变量的值的方法
3. 分段函数图象的作法
3.1.1 分段函数
高一
必修一
情景引入
某公共汽车的票价如下:(1)5公里以内(含5公里)票价2元;(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算)。如果一条线路的总长为30公里。
请回答下列问题:
1.我如果坐车到离起点15公里的地方,票价为多少元?如果坐车到离起点18公里的地方呢?
2.写出票价与里程之间的函数关系式,并画出函数图象。
本节目标
1. 了解简单的分段函数,会求分段函数的值.
2.会画简单的分段函数图象,会应用函数图象解决简单的问题.
任务一:知识预习
课前预习
(1)什么是分段函数?分段函数是一个还是几个函数?
(2)怎样求分段函数的值?如何画分段函数的图象?
预习课本,思考并完成以下问题
任务二:简单题型通关
课前预习
B
任务二:简单题型通关
课前预习
[1,+∞)
任务二:简单题型通关
课前预习
B
任务二:简单题型通关
课前预习
D
新知精讲
分段函数
新知精讲
知识点睛
题型探究
题型探究
题型探究
分类讨论
若|x|≤1,则|x-1|-2=
若|x|>1,则
所以x的值为
x=或x=
因为|x|≤1,所以x的值不存在
x=,符合|x|>1
归纳总结
类题通法
1.求分段
函数函数值的方法
2.求某条件下自变量的值的方法
(1)确定要求值的自变量属于哪一段区间.
(2)代入该段的解析式求值,当出现 f(f(x0))的形式时,应从内到外依次求值.
先假设所求的值在分段函数定义区间的各段上,然后相应求出自变量的值,切记代入检验.
活学活用
分类讨论
当0<a<1时
f(a)=f(a+1)
=2a
当a≥1时
2(a-1)=2a,无解
综上,f =6
C
f(a)=
a+1>1
f(a+1)=2(a+1-1)=2a
a=或a=0(舍去)
f=f(4)=2×(4-1)=6
f(a)=2(a-1)
a+1≥2
f(a+1)=2(a+1-1)=2a
活学活用
综上可知,x0= 或x0=10
当x0≤2时
f(x0)=+2=8,即=6
x0=或x0=(舍去)
当x0>2时
f(x0)=x0
x0=10
或10
题型探究
题点一:分段函数图象的作法
归纳总结
分段函数图象的画法
作分段函数的图象时,分别作出各段的图象,在作每一段图象时,先不管定义域的限制,作出其图象,再保留定义域内的一段图象即可,作图时要特别注意接点处点的虚实,保证不重不漏.
题型探究
题点二:由函数图象确定其解析式
当-1≤x<0时
当0≤x≤1时
设f(x)=ax+b
将(-1,0),(0,1)代入
设f(x)=kx
将(1,-1)代入,则k=-1
题型探究
[例4] 已知f(x)=|x-1|+|x+1|.
(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;
(3)写出该函数的值域.
题型探究
[例4] 已知f(x)=|x-1|+|x+1|.
(1)用分段函数的形式表示该函数;
当x≥1时
|x-1|=x-1
|x+1|=x+1
f(x)=(x-1)+(x+1)=2x
当-1<x<1时
|x-1|=1-x
|x+1|=x+1
f(x)=(1-x)+(x+1)=2
当x≤-1时
|x-1|=1-x
|x+1|=-x-1
f(x)=(1-x)+(-x-1)=-2x
题型探究
[例4] 已知f(x)=|x-1|+|x+1|.
(2)画出该函数的图象; (3)写出该函数的值域.
(2)图象如图:
(3)由函数图象可以得知函数的值域为[2,+∞).
归纳总结
对含有绝对值的函数,要作其图象,首先应根据绝对值的意义去掉绝对值符号,将函数转化为分段函数,然后分段作出函数图象.
类题通法
活学活用
画出函数f(x)的图象得值域是(-∞,1]
(-∞,1]
达标检测
D
达标检测
B
1<<6
f()=
达标检测
① √ 符合函数定义,且在定义域的不同区间,有不同的对应关系.
② × 当x=2时,f(2)=3或4,故不是函数.
③ × 当x=1时,f(1)=5或1,故不是函数.
④ √ 符合函数定义,且在定义域的不同区间,有不同的对应关系.
B
达标检测
A.-3 B.-1 C.1 D.3
f(1)=2
f(a)+f(1)=0
f(a)=-2
A
a肯定小于0
f(a)=a+1=-2
a=-3
本课小结
1. 求分段函数的函数值的方法
2. 求某条件下自变量的值的方法
3. 分段函数图象的作法
