人教B版(2019)数学必修第一册3.1.3 函数的奇偶性 课件(共36张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册3.1.3 函数的奇偶性 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 703.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 16:11:42 | ||
图片预览











文档简介
(共36张PPT)
3.1.3 函数的奇偶性
高一
必修一
本节目标
1.结合具体函数,了解函数奇偶性的含义.
2.理解函数奇偶性与图象的对称性之间的关系,会判断函数的奇偶性.
任务一:知识预习
课前预习
(1)偶函数与奇函数的定义分别是什么?
(2)奇、偶函数的定义域有什么特点?
(3)奇、偶函数的图象分别有什么特征?
预习课本,思考并完成以下问题
课前预习
任务二:简单题型通关
C
课前预习
任务二:简单题型通关
D
课前预习
任务二:简单题型通关
3.下列说法正确的是( )
A.如果一个函数的定义域关于坐标原点对称,则这个函数为奇函数
B.如果一个函数为偶函数,则它的定义域关于坐标原点对称
C.如果一个函数的定义域关于坐标原点对称,则这个函数为偶函数
D.如果一个函数的图象关于y轴对称,则这个函数为奇函数
B
课前预习
任务二:简单题型通关
4.已知f(x)是偶函数,且f(2)=2,则f(2)+f(-2)=________.
4
新知精讲
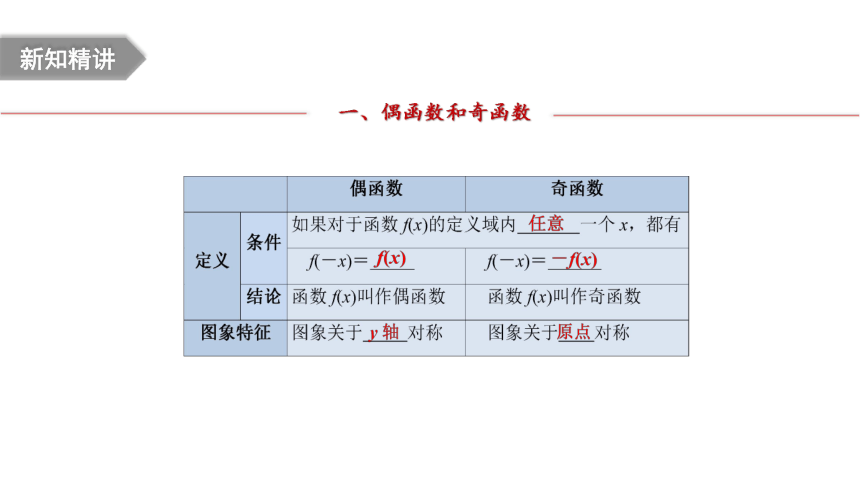
一、偶函数和奇函数
新知精讲
二、奇偶性
奇、偶函数的定义域关于原点对称,反之,若定义域不关于原点对称,则这个函数一定不具有奇偶性.
易错
提示
题型探究
题型一
判断函数的奇偶性
题型探究
函数f(x)的定义域为R,关于原点对称
第一步:确定定义域
第二步:验证
第三步:下结论
f(-x)=2-|-x|=2-|x|=f(x)
f(x)为偶函数
题型探究
定义域为{-1,1},关于原点对称,且f(x)=0
第一步:确定定义域
第二步:验证
第三步:下结论
f(-x)=-f(x),f(-x)=f(x)
f(x)既是奇函数又是偶函数
题型探究
定义域为{x|x≠1},不关于原点对称
第一步:确定定义域
第二步:下结论
f(x)是非奇非偶函数
题型探究
定义域是(-∞,0)∪(0,+∞),关于原点对称
第一步:确定定义域
第二步:验证
第三步:下结论
当x>0时,f(-x)=1-(-x)=1+x=f(x)
当x<0时,f(-x)=1+(-x)=1-x=f(x)
f(-x)=f(x),f(x)为偶函数
归纳总结
判断函数奇偶性的方法
1.定义法
2.图象法
3.性质法
①判断定义域是否关于原点对称
②验证f(-x)=-f(x)或f(-x)=f(x)
③下结论
①图象关于原点对称,则f(x)是奇函数
②图象关于y轴对称,则f(x)是偶函数
③图象既关于原点对称,又关于y轴对称,则f(x)既是奇函数,又是偶函数
④图象既不关于原点对称,又不关于y轴对称,则f(x)是非奇非偶函数
①偶函数的和、差、积、商(分母不为零)仍为偶函数
②奇函数的和、差仍为奇函数
③奇(偶)数个奇函数的积、商(分母不为零)为奇(偶)函数
④一个奇函数与一个偶函数的积为奇函数
活学活用
第一步:确定定义域
第二步:验证
第三步:下结论
x∈R,关于原点对称
f(-x)=(-x)2[(-x)2+2]=x2(x2+2)=f(x)
f(x)为偶函数
活学活用
第一步:确定定义域
第二步:验证
第三步:下结论
x∈R,关于原点对称
f(-x)=|-x+1|-|-x-1|
=-(|x+1|-|x-1|)=-f(x)
f(x)为奇函数
活学活用
第一步:确定定义域
第二步:验证
第三步:下结论
定义域为[-1,0)∪(0,1],关于原点对称
f(x)为奇函数
题型探究
题型二
利用函数的奇偶性
求
参数
[例2] (1)若函数f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a=________,b=________;
(2)已知函数f(x)=ax2+2x是奇函数,则实数a=________.
题型探究
[例2] (1)若函数f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a=________,b=________;
f(x)的定义域关于原点对称
a-1=-2a
a=
f(x)=x2+bx+b+1为二次函数
f(x)为偶函数
b=0
0
题型探究
[例2] (2)已知函数 f(x)=ax2+2x是奇函数,则实数a=________.
f(-x)+f(x)=0
a(-x)2+2(-x)+ax2+2x=2ax2=0
a=0
0
归纳总结
利用奇偶性求参数的常见类型
(1)定义域含参数:奇偶函数f(x)的定义域为[a,b],根据定义域关于原点对称,利用a+b=0求参数.
(2)解析式含参数:根据f(-x)=-f(x)或f(-x)=f(x)列式,比较系数利用待定系数法求解.
活学活用
-1
题型探究
题型三
利用函数的奇偶性
求
解析式
[例3] 若f(x)是定义在R上的奇函数,当x>0时,f(x)=x2-2x+3,求f(x)的解析式.
x<0时,f(-x)=(-x)2-2(-x)+3=x2+2x+3
f(x)=-f(-x)
f(x)=-x2-2x-3
题型探究
一题多变
思维发散
[例3] 若f(x)是定义在R上的奇函数,当x>0时,f(x)=x2-2x+3,求f(x)的解析式.
1.[变设问]本例条件不变,求f(-2)的值.
f(-2)=-f(2)=-(22-2×2+3)=-3
题型探究
一题多变
思维发散
[例3] 若f(x)是定义在R上的奇函数,当x>0时,f(x)=x2-2x+3,求f(x)的解析式.
2.[变条件]把本例中的奇函数改为偶函数,其他条件不变,求当x<0时,f(x)的解析式.
当x<0时,f(-x)=(-x)2-2(-x)+3=x2+2x+3
f(x)是偶函数
f(x)=f(-x)
f(x)=x2+2x+3
归纳总结
利用函数奇偶性求函数解析式3个步骤
(1)“求谁设谁”,即在哪个区间上求解析式,x就应在哪个区间上设;
(2)转化到已知区间上,代入已知的解析式;
(3)利用f(x)的奇偶性写出-f(x)或f(-x),从而解出f(x).
题型探究
题型四
函数单调性与奇偶性
综合
题点一:比较大小问题
1.已知偶函数f(x)在[0,+∞)上单调递减,则f(1)和f(-10)的大小关系为( )
A.f(1)>f(-10) B.f(1)C.f(1)=f(-10) D.f(1)和f(-10)关系不定
一题多联题根显现
f(x)是偶函数
f(-10)=f(10)
f(x)在[0,+∞)上单调递减
f(1)>f(10)
f(1)>f(-10)
A
题型探究
题型四
函数单调性与奇偶性
综合
题点二:区间内的最值问题
2.若奇函数f(x)在区间[2,5]上的最小值是6,那么f(x)在区间[-5,-2]上有 ( )
A.最小值6 B.最小值-6
C.最大值-6 D.最大值6
一题多联题根显现
C
奇函数f(x)在[2,5]上有最小值6,所以可设a∈[2,5],有f(a)=6.由奇函数的性质,f(x)在[-5,-2]上必有最大值,且最大值为f(-a)=-f(a)=-6
题型探究
题型四
函数单调性与奇偶性
综合
题点三:解不等式问题
3.设定义在[-2,2]上的奇函数f(x)在区间[0,2]上是减函数,若 f(1-m)<f(m),求实数m的取值范围.
一题多联题根显现
f(x)是奇函数
f(x)在[0,2]上是减函数
f(x)在[-2,2]上是减函数
f(1-m)归纳总结
函数的奇偶性与单调性的综合问题解题思路
(1)解决比较大小、最值问题应充分利用奇函数在关于原点对称的两个区间上具有相同的单调性,偶函数在关于原点对称的两个区间上具有相反的单调性.
(2)解决不等式问题时一定要充分利用已知的条件,把已知不等式转化成f(x1)>f(x2)或f(x1)达标检测
由偶函数定义知f(x)=|x-1|+|x+1|是偶函数
D
达标检测
定义域关于原点对称
f(x)是奇函数
图象关于原点对称
B
达标检测
3.已知f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,且f(2)=0,
则使f(x)<0的x的取值范围是( )
A.(-∞,2) B.(2,+∞)
C.(-∞,-2)∪(2,+∞) D.(-2,2)
如图所示
D
遇到以偶函数为背景的此类题目,画出不含坐标轴的二次函数简图.若f(x)在(-∞,0]上递减,则开口向上,若f(x)在(-∞,0]上递增,则开口向下
方法总结
达标检测
B
设x<0,则-x>0,
∵f(x)是奇函数,
∴f(x)=-f(-x)=-[(-x)(1+x)]=x(1+x)
本课小结
1、偶函数与奇函数的定义分别是什么?有什么性质
2、怎样判断函数的奇偶性?
3.1.3 函数的奇偶性
高一
必修一
本节目标
1.结合具体函数,了解函数奇偶性的含义.
2.理解函数奇偶性与图象的对称性之间的关系,会判断函数的奇偶性.
任务一:知识预习
课前预习
(1)偶函数与奇函数的定义分别是什么?
(2)奇、偶函数的定义域有什么特点?
(3)奇、偶函数的图象分别有什么特征?
预习课本,思考并完成以下问题
课前预习
任务二:简单题型通关
C
课前预习
任务二:简单题型通关
D
课前预习
任务二:简单题型通关
3.下列说法正确的是( )
A.如果一个函数的定义域关于坐标原点对称,则这个函数为奇函数
B.如果一个函数为偶函数,则它的定义域关于坐标原点对称
C.如果一个函数的定义域关于坐标原点对称,则这个函数为偶函数
D.如果一个函数的图象关于y轴对称,则这个函数为奇函数
B
课前预习
任务二:简单题型通关
4.已知f(x)是偶函数,且f(2)=2,则f(2)+f(-2)=________.
4
新知精讲
一、偶函数和奇函数
新知精讲
二、奇偶性
奇、偶函数的定义域关于原点对称,反之,若定义域不关于原点对称,则这个函数一定不具有奇偶性.
易错
提示
题型探究
题型一
判断函数的奇偶性
题型探究
函数f(x)的定义域为R,关于原点对称
第一步:确定定义域
第二步:验证
第三步:下结论
f(-x)=2-|-x|=2-|x|=f(x)
f(x)为偶函数
题型探究
定义域为{-1,1},关于原点对称,且f(x)=0
第一步:确定定义域
第二步:验证
第三步:下结论
f(-x)=-f(x),f(-x)=f(x)
f(x)既是奇函数又是偶函数
题型探究
定义域为{x|x≠1},不关于原点对称
第一步:确定定义域
第二步:下结论
f(x)是非奇非偶函数
题型探究
定义域是(-∞,0)∪(0,+∞),关于原点对称
第一步:确定定义域
第二步:验证
第三步:下结论
当x>0时,f(-x)=1-(-x)=1+x=f(x)
当x<0时,f(-x)=1+(-x)=1-x=f(x)
f(-x)=f(x),f(x)为偶函数
归纳总结
判断函数奇偶性的方法
1.定义法
2.图象法
3.性质法
①判断定义域是否关于原点对称
②验证f(-x)=-f(x)或f(-x)=f(x)
③下结论
①图象关于原点对称,则f(x)是奇函数
②图象关于y轴对称,则f(x)是偶函数
③图象既关于原点对称,又关于y轴对称,则f(x)既是奇函数,又是偶函数
④图象既不关于原点对称,又不关于y轴对称,则f(x)是非奇非偶函数
①偶函数的和、差、积、商(分母不为零)仍为偶函数
②奇函数的和、差仍为奇函数
③奇(偶)数个奇函数的积、商(分母不为零)为奇(偶)函数
④一个奇函数与一个偶函数的积为奇函数
活学活用
第一步:确定定义域
第二步:验证
第三步:下结论
x∈R,关于原点对称
f(-x)=(-x)2[(-x)2+2]=x2(x2+2)=f(x)
f(x)为偶函数
活学活用
第一步:确定定义域
第二步:验证
第三步:下结论
x∈R,关于原点对称
f(-x)=|-x+1|-|-x-1|
=-(|x+1|-|x-1|)=-f(x)
f(x)为奇函数
活学活用
第一步:确定定义域
第二步:验证
第三步:下结论
定义域为[-1,0)∪(0,1],关于原点对称
f(x)为奇函数
题型探究
题型二
利用函数的奇偶性
求
参数
[例2] (1)若函数f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a=________,b=________;
(2)已知函数f(x)=ax2+2x是奇函数,则实数a=________.
题型探究
[例2] (1)若函数f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a=________,b=________;
f(x)的定义域关于原点对称
a-1=-2a
a=
f(x)=x2+bx+b+1为二次函数
f(x)为偶函数
b=0
0
题型探究
[例2] (2)已知函数 f(x)=ax2+2x是奇函数,则实数a=________.
f(-x)+f(x)=0
a(-x)2+2(-x)+ax2+2x=2ax2=0
a=0
0
归纳总结
利用奇偶性求参数的常见类型
(1)定义域含参数:奇偶函数f(x)的定义域为[a,b],根据定义域关于原点对称,利用a+b=0求参数.
(2)解析式含参数:根据f(-x)=-f(x)或f(-x)=f(x)列式,比较系数利用待定系数法求解.
活学活用
-1
题型探究
题型三
利用函数的奇偶性
求
解析式
[例3] 若f(x)是定义在R上的奇函数,当x>0时,f(x)=x2-2x+3,求f(x)的解析式.
x<0时,f(-x)=(-x)2-2(-x)+3=x2+2x+3
f(x)=-f(-x)
f(x)=-x2-2x-3
题型探究
一题多变
思维发散
[例3] 若f(x)是定义在R上的奇函数,当x>0时,f(x)=x2-2x+3,求f(x)的解析式.
1.[变设问]本例条件不变,求f(-2)的值.
f(-2)=-f(2)=-(22-2×2+3)=-3
题型探究
一题多变
思维发散
[例3] 若f(x)是定义在R上的奇函数,当x>0时,f(x)=x2-2x+3,求f(x)的解析式.
2.[变条件]把本例中的奇函数改为偶函数,其他条件不变,求当x<0时,f(x)的解析式.
当x<0时,f(-x)=(-x)2-2(-x)+3=x2+2x+3
f(x)是偶函数
f(x)=f(-x)
f(x)=x2+2x+3
归纳总结
利用函数奇偶性求函数解析式3个步骤
(1)“求谁设谁”,即在哪个区间上求解析式,x就应在哪个区间上设;
(2)转化到已知区间上,代入已知的解析式;
(3)利用f(x)的奇偶性写出-f(x)或f(-x),从而解出f(x).
题型探究
题型四
函数单调性与奇偶性
综合
题点一:比较大小问题
1.已知偶函数f(x)在[0,+∞)上单调递减,则f(1)和f(-10)的大小关系为( )
A.f(1)>f(-10) B.f(1)
一题多联题根显现
f(x)是偶函数
f(-10)=f(10)
f(x)在[0,+∞)上单调递减
f(1)>f(10)
f(1)>f(-10)
A
题型探究
题型四
函数单调性与奇偶性
综合
题点二:区间内的最值问题
2.若奇函数f(x)在区间[2,5]上的最小值是6,那么f(x)在区间[-5,-2]上有 ( )
A.最小值6 B.最小值-6
C.最大值-6 D.最大值6
一题多联题根显现
C
奇函数f(x)在[2,5]上有最小值6,所以可设a∈[2,5],有f(a)=6.由奇函数的性质,f(x)在[-5,-2]上必有最大值,且最大值为f(-a)=-f(a)=-6
题型探究
题型四
函数单调性与奇偶性
综合
题点三:解不等式问题
3.设定义在[-2,2]上的奇函数f(x)在区间[0,2]上是减函数,若 f(1-m)<f(m),求实数m的取值范围.
一题多联题根显现
f(x)是奇函数
f(x)在[0,2]上是减函数
f(x)在[-2,2]上是减函数
f(1-m)
函数的奇偶性与单调性的综合问题解题思路
(1)解决比较大小、最值问题应充分利用奇函数在关于原点对称的两个区间上具有相同的单调性,偶函数在关于原点对称的两个区间上具有相反的单调性.
(2)解决不等式问题时一定要充分利用已知的条件,把已知不等式转化成f(x1)>f(x2)或f(x1)
由偶函数定义知f(x)=|x-1|+|x+1|是偶函数
D
达标检测
定义域关于原点对称
f(x)是奇函数
图象关于原点对称
B
达标检测
3.已知f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,且f(2)=0,
则使f(x)<0的x的取值范围是( )
A.(-∞,2) B.(2,+∞)
C.(-∞,-2)∪(2,+∞) D.(-2,2)
如图所示
D
遇到以偶函数为背景的此类题目,画出不含坐标轴的二次函数简图.若f(x)在(-∞,0]上递减,则开口向上,若f(x)在(-∞,0]上递增,则开口向下
方法总结
达标检测
B
设x<0,则-x>0,
∵f(x)是奇函数,
∴f(x)=-f(-x)=-[(-x)(1+x)]=x(1+x)
本课小结
1、偶函数与奇函数的定义分别是什么?有什么性质
2、怎样判断函数的奇偶性?
