人教B版(2019)数学必修第一册3.1.2 函数的单调性 课件(共27张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册3.1.2 函数的单调性 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 16:12:57 | ||
图片预览







文档简介
(共27张PPT)
3.1.2 函数的单调性
高一
必修一
情景引入
上图为股市中,某股票在半天内的行情,请描述此股票的涨幅情况。
本节目标
1.通过已学过的函数特别是二次函数,理解函数的单调性及其几何意义.
2.学会运用函数图象理解和研究函数的性质.
3.能够熟练应用定义判断与证明函数在某区间上的单调性.
任务一:知识预习
课前预习
(1)增函数、减函数的概念是什么?
(2)如何表示函数的单调区间?
(3)函数的单调性和单调区间有什么关系?
预习课本,思考并完成以下问题
任务二:简单题型通关
课前预习
C
任务二:简单题型通关
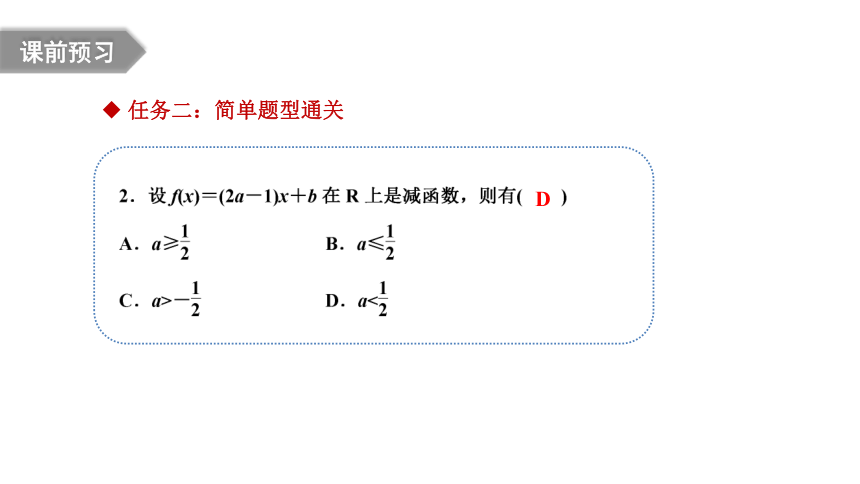
课前预习
D
任务二:简单题型通关
课前预习
B
任务二:简单题型通关
课前预习
[1,+∞)
(-∞,1]
新知精讲
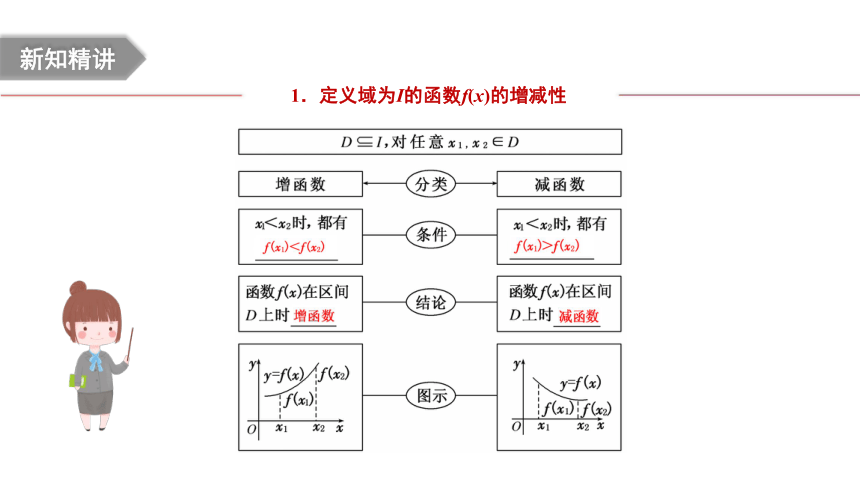
1.定义域为I的函数f(x)的增减性
新知精讲
要点提示
定义中的x1,x2有以下3个特征:
(1)任意性,即“任意取x1,x2”中“任意”二字绝不能去掉,证明时不能以特殊代替一般;
(2)有大小,通常规定x1<x2;
(3)属于同一个单调区间.
如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间上具有(严格的)________,区间D叫做y=f(x)的_________.
新知精讲
2.单调性与单调区间
一个函数出现两个或者两个以上的单调区间时,不能用“∪”连接,而应该用“和”连接.如函数y=在(-∞,0)和(0,+∞)上单调递减,却不能表述为:函数y=在(-∞,0)∪(0,+∞)上单调递减.
易错提示
题型探究
题型一 函数单调性的判定与证明
例1 求证:函数f(x)=在(0,+∞)上是减函数,在(-∞,0)上是增函数.
1.证在(-∞,0)上是增函数
f (x1)-f (x2)<0
f (x1)在(-∞,0)上是增函数
对于任意的x1,x2∈(0,+∞),且x1f(x1)-f(x2)>0
f(x1)>f(x2)
在(0,+∞)上是减函数
2.证在(0,+∞)上是减函数
归纳总结
利用定义证明函数单调性的4个步骤
活学活用
1.证明函数f(x)=x+在(0,1)上是减函数.
设x1,x2是区间(0,1)上的任意两个实数,且x10f(x1)-f(x2)>0
f(x1)>f(x2)
f(x)=x+ 在(0,1)上是减函数
题型探究
题型二 求函数的单调性区间
例2 画出函数 y=-x2+2|x|+1的图象并写出函数的单调区间.
单调增区间为(-∞,-1],[0,1]
单调减区间为(-1,0),(1,+∞)
归纳总结
求函数单调区间的2种方法
法一
定义法
法二
图象法
即先求出定义域,再利用定义法进行判断求解
先画出图象,根据图象求单调区间
活学活用
2.如图所示为函数y=f(x),x∈[-4,7]的图象,则函数f(x)的单调递增区间是________________.
[-1.5,3]和[5,6]
活学活用
函数f(x)=的定义域为(-∞,1)∪(1,+∞)
设x1,x2∈(-∞,1),且x1x1f(x1)-f(x2)>0
f(x1)>f(x2)
f(x)在(-∞,1)上单调递减
同理函数f(x)在(1,+∞)上单调递减
函数f(x)的单调递减区间是(-∞,1),(1,+∞)
题型探究
题点一:利用单调性比较大小
例3 若函数f(x)在区间(-∞,+∞)上是减函数,则下列关系式一定成立的是( )
A.f(a)>f(2a) B.f(a2)<f(a)
C.f(a2+a)<f(a) D.f(a2+1)<f(a2)
f(x)是区间(-∞,+∞)上的减函数
a2+1>a2
f(a2+1)<f(a2)
D
题型探究
题点二:利用单调性解不等式
例4 已知函数y=f(x)是(-∞,+∞)上的增函数,且 f(2x-3)>f(5x+6),求实数x的取值范围.
y=f(x)是(-∞,+∞)上的增函数
f(2x-3)>f(5x+6)
2x-3>5x+6
x<-3
题型探究
题点三:已知单调性求参数范围
例5 已知函数f(x)=x-+在(1,+∞)上是增函数,求实数a的取值范围.
设1f(x)在(1,+∞)上是增函数
f(x1)-f(x2)=(x1-x2) <0
x1-x2<0
>0
a>-x1x2
x1x2>1
-x1x2<-1
a≥-1
归纳总结
函数单调性的应用
(1)函数单调性定义的“双向性”:利用定义可以判断、证明函数的单调性,反过来,若已知函数的单调性可以确定函数中参数的取值范围.
(2)若一个函数在区间[a,b]上是单调的,则此函数在这一单调区间内的任意子集上也是单调的.
达标检测
1.若函数f(x)的定义域为R,且在(0,+∞)上是减函数,则下列不等式成立的是( )
A.f()>f(a2-a+1) B.f()≥f(a2-a+1)
C.f()B
a2-a+1=
f(x)在(0,+∞)上是减函数
f(a2-a+1)≤f()
达标检测
2.函数 f(x)=x|x-2| 的增区间是( )
A.(-∞,1] B.[2,+∞)
C.(-∞,1],[2,+∞) D.(-∞,+∞)
C
f(x)=x|x-2|=
作出f(x)简图如图:
由图象可知f(x)的增区间是(-∞,1],[2,+∞)
达标检测
3.设函数f(x)是R上的减函数,若 f(m-1)>f(2m-1),则实数m的取值范围是________.
f(x)是R上的减函数
f(m-1)>f(2m-1)
m-1<2m-1
m>0
达标检测
本课小结
1. 增函数、减函数的概念
2. 利用定义证明函数单调性的方法
3. 求函数单调区间的方法
3.1.2 函数的单调性
高一
必修一
情景引入
上图为股市中,某股票在半天内的行情,请描述此股票的涨幅情况。
本节目标
1.通过已学过的函数特别是二次函数,理解函数的单调性及其几何意义.
2.学会运用函数图象理解和研究函数的性质.
3.能够熟练应用定义判断与证明函数在某区间上的单调性.
任务一:知识预习
课前预习
(1)增函数、减函数的概念是什么?
(2)如何表示函数的单调区间?
(3)函数的单调性和单调区间有什么关系?
预习课本,思考并完成以下问题
任务二:简单题型通关
课前预习
C
任务二:简单题型通关
课前预习
D
任务二:简单题型通关
课前预习
B
任务二:简单题型通关
课前预习
[1,+∞)
(-∞,1]
新知精讲
1.定义域为I的函数f(x)的增减性
新知精讲
要点提示
定义中的x1,x2有以下3个特征:
(1)任意性,即“任意取x1,x2”中“任意”二字绝不能去掉,证明时不能以特殊代替一般;
(2)有大小,通常规定x1<x2;
(3)属于同一个单调区间.
如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间上具有(严格的)________,区间D叫做y=f(x)的_________.
新知精讲
2.单调性与单调区间
一个函数出现两个或者两个以上的单调区间时,不能用“∪”连接,而应该用“和”连接.如函数y=在(-∞,0)和(0,+∞)上单调递减,却不能表述为:函数y=在(-∞,0)∪(0,+∞)上单调递减.
易错提示
题型探究
题型一 函数单调性的判定与证明
例1 求证:函数f(x)=在(0,+∞)上是减函数,在(-∞,0)上是增函数.
1.证在(-∞,0)上是增函数
f (x1)-f (x2)<0
f (x1)
对于任意的x1,x2∈(0,+∞),且x1
f(x1)>f(x2)
在(0,+∞)上是减函数
2.证在(0,+∞)上是减函数
归纳总结
利用定义证明函数单调性的4个步骤
活学活用
1.证明函数f(x)=x+在(0,1)上是减函数.
设x1,x2是区间(0,1)上的任意两个实数,且x1
f(x1)>f(x2)
f(x)=x+ 在(0,1)上是减函数
题型探究
题型二 求函数的单调性区间
例2 画出函数 y=-x2+2|x|+1的图象并写出函数的单调区间.
单调增区间为(-∞,-1],[0,1]
单调减区间为(-1,0),(1,+∞)
归纳总结
求函数单调区间的2种方法
法一
定义法
法二
图象法
即先求出定义域,再利用定义法进行判断求解
先画出图象,根据图象求单调区间
活学活用
2.如图所示为函数y=f(x),x∈[-4,7]的图象,则函数f(x)的单调递增区间是________________.
[-1.5,3]和[5,6]
活学活用
函数f(x)=的定义域为(-∞,1)∪(1,+∞)
设x1,x2∈(-∞,1),且x1
f(x1)>f(x2)
f(x)在(-∞,1)上单调递减
同理函数f(x)在(1,+∞)上单调递减
函数f(x)的单调递减区间是(-∞,1),(1,+∞)
题型探究
题点一:利用单调性比较大小
例3 若函数f(x)在区间(-∞,+∞)上是减函数,则下列关系式一定成立的是( )
A.f(a)>f(2a) B.f(a2)<f(a)
C.f(a2+a)<f(a) D.f(a2+1)<f(a2)
f(x)是区间(-∞,+∞)上的减函数
a2+1>a2
f(a2+1)<f(a2)
D
题型探究
题点二:利用单调性解不等式
例4 已知函数y=f(x)是(-∞,+∞)上的增函数,且 f(2x-3)>f(5x+6),求实数x的取值范围.
y=f(x)是(-∞,+∞)上的增函数
f(2x-3)>f(5x+6)
2x-3>5x+6
x<-3
题型探究
题点三:已知单调性求参数范围
例5 已知函数f(x)=x-+在(1,+∞)上是增函数,求实数a的取值范围.
设1
f(x1)-f(x2)=(x1-x2) <0
x1-x2<0
>0
a>-x1x2
x1x2>1
-x1x2<-1
a≥-1
归纳总结
函数单调性的应用
(1)函数单调性定义的“双向性”:利用定义可以判断、证明函数的单调性,反过来,若已知函数的单调性可以确定函数中参数的取值范围.
(2)若一个函数在区间[a,b]上是单调的,则此函数在这一单调区间内的任意子集上也是单调的.
达标检测
1.若函数f(x)的定义域为R,且在(0,+∞)上是减函数,则下列不等式成立的是( )
A.f()>f(a2-a+1) B.f()≥f(a2-a+1)
C.f()
a2-a+1=
f(x)在(0,+∞)上是减函数
f(a2-a+1)≤f()
达标检测
2.函数 f(x)=x|x-2| 的增区间是( )
A.(-∞,1] B.[2,+∞)
C.(-∞,1],[2,+∞) D.(-∞,+∞)
C
f(x)=x|x-2|=
作出f(x)简图如图:
由图象可知f(x)的增区间是(-∞,1],[2,+∞)
达标检测
3.设函数f(x)是R上的减函数,若 f(m-1)>f(2m-1),则实数m的取值范围是________.
f(x)是R上的减函数
f(m-1)>f(2m-1)
m-1<2m-1
m>0
达标检测
本课小结
1. 增函数、减函数的概念
2. 利用定义证明函数单调性的方法
3. 求函数单调区间的方法
