人教B版(2019)数学必修第一册3.1.1函数的概念 课件(共34张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第一册3.1.1函数的概念 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 16:15:26 | ||
图片预览











文档简介
(共34张PPT)
3.1.1 函数的概念
高一
必修一
本节目标
1 .理解函数的概念,了解函数构成的三要素.
2.会求一些简单函数的定义域、值域.
任务一:知识预习
课前预习
(1)在集合的观点下函数是如何定义?函数有哪三要素?
(2)相等函数是指什么样的函数?
预习课本,思考并完成以下问题
任务二:简单题型通关
课前预习
1.设函数f(x)=3x4-1,则f(a)-f(-a)=( )
A.0 B.3a4-1
C.6a4-2 D.6a4
A
任务二:简单题型通关
课前预习
2.下列函数f(x)与g(x)表示同一个函数的是( )
A.f(x)=与g(x)=3x
B.f(x)=x;g(x)=
C.f(x)=x2;g(x)=(x+1)2
D.f(x)=|x|;g(x)=
D
定义域不同
×
对应关系不同
×
对应关系不同
×
√
任务二:简单题型通关
课前预习
3.函数y=的定义域为A,函数y=的值域是B,则A∩B=________________(用区间表示).
[0,1)∪(1,+∞)
新知精讲
函数的概念
新知精讲
函数的概念
新知精讲
函数的概念
对函数概念的3点说明
(1)当A,B为非空数集时,符号“f:A→B”表示A到B的一个函数.
(2)集合A中的数具有任意性,集合B中的数具有唯一性.
(3)符号“f”它表示对应关系,在不同的函数中f的具体含义不一样.
题型探究
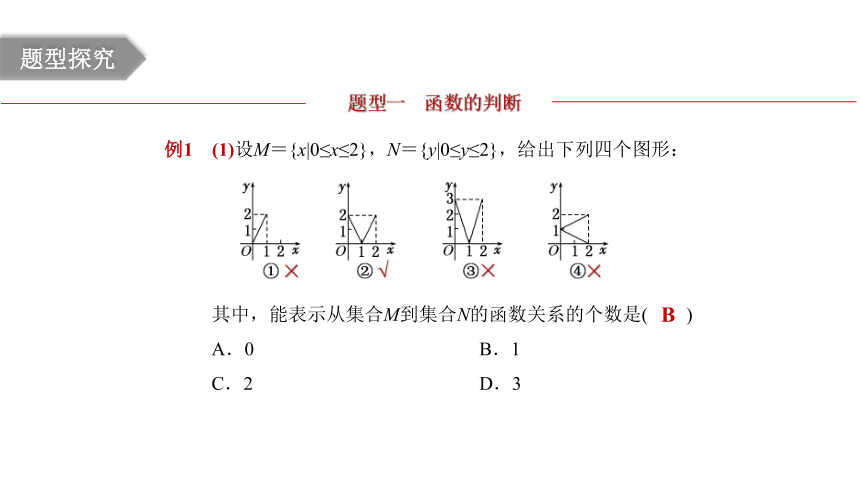
题型一 函数的判断
例1 (1)设M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形:
其中,能表示从集合M到集合N的函数关系的个数是( )
A.0 B.1
C.2 D.3
×
√
×
×
B
题型探究
题型一 函数的判断
√
√
×
×
x=0时,的值不存在
x<0时,的值不存在
归纳总结
1.判断对应关系是否为函数的2个条件
(1)A,B必须是非空数集.
(2)A中任意一元素在B中有且只有一个元素与之对应.
对应关系是“一对一”或“多对一”的是函数关系,“一对多”的不是函数关系.
归纳总结
2.根据图形判断是否为函数的方法
(1)任取一条垂直于x轴的直线l.
(2)在定义域内平行移动直线l.
(3)若l与图形有且只有一个交点,则是函数;若在定义域内没有交点或有两个或两个以上的交点,则不是函数.
活学活用
对任意x∈A,y值不唯一
×
2∈A,在B中找不到
与之相对应的数
-1∈A,在B中找不到
与之相对应的数
√
×
×
B
题型探究
题型二 相等函数
定义域不同
×
√
定义域不同
×
对应关系不同
×
B
考点透视:若两函数的定义域和对应关系都相同,则这两个函数为相等函数。
归纳总结
判断函数相等的方法
判断函数是否相等,关键是树立定义域优先的原则.
(1)先看定义域,若定义域不同,则不相等;
(2)若定义域相同,再化简函数的解析式,看对应关系是否相同.
活学活用
√
定义域不同
×
√
对应关系不同
×
题型探究
题型三 求函数的定义域
例3 求下列函数的定义域
{x|x≤1,且x≠-1}
{x|x≤5,且x≠±3}
类题通法
求函数定义域的常用方法
(1)若f(x)是分式,则应考虑使分母不为零.
(2)若f(x)是偶次根式,则被开方数大于或等于零.
(3)若f(x)是指数幂,则函数的定义域是使幂运算有意义的实数集合.
(4)若f(x)是由几个式子构成的,则函数的定义域是几个部分定义域的交集.
(5)若f(x)是实际问题的解析式,则应符合实际问题,使实际问题有意义.
活学活用
3.求下列函数的定义域:
x-2≠0
定义域为{x|x≠2}
定义域为{x|1≤x≤3}
定义域为{x|x>-1,且x≠1}
题型探究
题型四 求函数值和值域
例4 (1)已知 f(x)=(x∈R,且x≠-1),g(x)=x2+2(x∈R),则f(2)=________,f(g(2))=________.
f(2)==
g (2)=22+2=6
f ( g(2))=f (6)==
题型探究
题型四 求函数值和值域
题型探究
题型四 求函数值和值域
x∈R
x+1∈R
函数值域是R
题型探究
题型四 求函数值和值域
y=x2-2x+3=(x-1)2+2,x∈[0,3)
函数的值域为[2,6)
配方法
题型探究
题型四 求函数值和值域
分离常数法
≠0
值域为{y|y∈R且y≠3}
题型探究
题型四 求函数值和值域
换元法
设t=
t≥0且x=t2+1
y=2(t2+1)-t=2+
函数的值域为
类题通法
1.函数求值的方法
(1)已知f(x)的表达式时,只需用a替换表达式中的x即得f(a)的值.
(2)求f(g(a))的值应遵循由里往外的原则.
类题通法
2.求函数值域常用的4种方法
(1)观察法:对于一些比较简单的函数,其值域可通过观察得到;
(2)配方法:当所给函数是二次函数或可化为二次函数时,可利用配方法求其值域;
(3)分离常数法:此方法主要是针对有理分式,即将有理分式转化为“反比例函数类”的形式,便于求值域;
(4)换元法:即运用新元代换,将所给函数化成值域易确定的函数.对于f(x)=ax+b+(其中a,b,c,d为常数,且a≠0)型的函数常用换元法.
活学活用
x2+1≥1
0<≤2
函数的值域为(-1,1]
+1≥1
函数的值域为[1,+∞)
达标检测
A
达标检测
B
达标检测
定义域不同
×
√
对应关系不同
值域不同
×
×
C
达标检测
(1) f(x)的定义域是(-∞,0)∪(0,+∞)
(2) f(-1)=-1+=-2
f(2)=2+=
(3)当a≠-1时,a+1≠0
f(a+1)=a+1+
本课小结
1. 判断对应关系是否为函数的条件
2. 判断函数相等的方法
3. 求函数定义域的常用方法
4.求函数值域常用的4种方法
3.1.1 函数的概念
高一
必修一
本节目标
1 .理解函数的概念,了解函数构成的三要素.
2.会求一些简单函数的定义域、值域.
任务一:知识预习
课前预习
(1)在集合的观点下函数是如何定义?函数有哪三要素?
(2)相等函数是指什么样的函数?
预习课本,思考并完成以下问题
任务二:简单题型通关
课前预习
1.设函数f(x)=3x4-1,则f(a)-f(-a)=( )
A.0 B.3a4-1
C.6a4-2 D.6a4
A
任务二:简单题型通关
课前预习
2.下列函数f(x)与g(x)表示同一个函数的是( )
A.f(x)=与g(x)=3x
B.f(x)=x;g(x)=
C.f(x)=x2;g(x)=(x+1)2
D.f(x)=|x|;g(x)=
D
定义域不同
×
对应关系不同
×
对应关系不同
×
√
任务二:简单题型通关
课前预习
3.函数y=的定义域为A,函数y=的值域是B,则A∩B=________________(用区间表示).
[0,1)∪(1,+∞)
新知精讲
函数的概念
新知精讲
函数的概念
新知精讲
函数的概念
对函数概念的3点说明
(1)当A,B为非空数集时,符号“f:A→B”表示A到B的一个函数.
(2)集合A中的数具有任意性,集合B中的数具有唯一性.
(3)符号“f”它表示对应关系,在不同的函数中f的具体含义不一样.
题型探究
题型一 函数的判断
例1 (1)设M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形:
其中,能表示从集合M到集合N的函数关系的个数是( )
A.0 B.1
C.2 D.3
×
√
×
×
B
题型探究
题型一 函数的判断
√
√
×
×
x=0时,的值不存在
x<0时,的值不存在
归纳总结
1.判断对应关系是否为函数的2个条件
(1)A,B必须是非空数集.
(2)A中任意一元素在B中有且只有一个元素与之对应.
对应关系是“一对一”或“多对一”的是函数关系,“一对多”的不是函数关系.
归纳总结
2.根据图形判断是否为函数的方法
(1)任取一条垂直于x轴的直线l.
(2)在定义域内平行移动直线l.
(3)若l与图形有且只有一个交点,则是函数;若在定义域内没有交点或有两个或两个以上的交点,则不是函数.
活学活用
对任意x∈A,y值不唯一
×
2∈A,在B中找不到
与之相对应的数
-1∈A,在B中找不到
与之相对应的数
√
×
×
B
题型探究
题型二 相等函数
定义域不同
×
√
定义域不同
×
对应关系不同
×
B
考点透视:若两函数的定义域和对应关系都相同,则这两个函数为相等函数。
归纳总结
判断函数相等的方法
判断函数是否相等,关键是树立定义域优先的原则.
(1)先看定义域,若定义域不同,则不相等;
(2)若定义域相同,再化简函数的解析式,看对应关系是否相同.
活学活用
√
定义域不同
×
√
对应关系不同
×
题型探究
题型三 求函数的定义域
例3 求下列函数的定义域
{x|x≤1,且x≠-1}
{x|x≤5,且x≠±3}
类题通法
求函数定义域的常用方法
(1)若f(x)是分式,则应考虑使分母不为零.
(2)若f(x)是偶次根式,则被开方数大于或等于零.
(3)若f(x)是指数幂,则函数的定义域是使幂运算有意义的实数集合.
(4)若f(x)是由几个式子构成的,则函数的定义域是几个部分定义域的交集.
(5)若f(x)是实际问题的解析式,则应符合实际问题,使实际问题有意义.
活学活用
3.求下列函数的定义域:
x-2≠0
定义域为{x|x≠2}
定义域为{x|1≤x≤3}
定义域为{x|x>-1,且x≠1}
题型探究
题型四 求函数值和值域
例4 (1)已知 f(x)=(x∈R,且x≠-1),g(x)=x2+2(x∈R),则f(2)=________,f(g(2))=________.
f(2)==
g (2)=22+2=6
f ( g(2))=f (6)==
题型探究
题型四 求函数值和值域
题型探究
题型四 求函数值和值域
x∈R
x+1∈R
函数值域是R
题型探究
题型四 求函数值和值域
y=x2-2x+3=(x-1)2+2,x∈[0,3)
函数的值域为[2,6)
配方法
题型探究
题型四 求函数值和值域
分离常数法
≠0
值域为{y|y∈R且y≠3}
题型探究
题型四 求函数值和值域
换元法
设t=
t≥0且x=t2+1
y=2(t2+1)-t=2+
函数的值域为
类题通法
1.函数求值的方法
(1)已知f(x)的表达式时,只需用a替换表达式中的x即得f(a)的值.
(2)求f(g(a))的值应遵循由里往外的原则.
类题通法
2.求函数值域常用的4种方法
(1)观察法:对于一些比较简单的函数,其值域可通过观察得到;
(2)配方法:当所给函数是二次函数或可化为二次函数时,可利用配方法求其值域;
(3)分离常数法:此方法主要是针对有理分式,即将有理分式转化为“反比例函数类”的形式,便于求值域;
(4)换元法:即运用新元代换,将所给函数化成值域易确定的函数.对于f(x)=ax+b+(其中a,b,c,d为常数,且a≠0)型的函数常用换元法.
活学活用
x2+1≥1
0<≤2
函数的值域为(-1,1]
+1≥1
函数的值域为[1,+∞)
达标检测
A
达标检测
B
达标检测
定义域不同
×
√
对应关系不同
值域不同
×
×
C
达标检测
(1) f(x)的定义域是(-∞,0)∪(0,+∞)
(2) f(-1)=-1+=-2
f(2)=2+=
(3)当a≠-1时,a+1≠0
f(a+1)=a+1+
本课小结
1. 判断对应关系是否为函数的条件
2. 判断函数相等的方法
3. 求函数定义域的常用方法
4.求函数值域常用的4种方法
