6.3二次函数复习 课件

课件31张PPT。复习：二次函数复习要点巩固训练能力训练例题讲解归纳小结退出二次函数（复习）一、定义二、顶点与对称轴三、解析式的求法四、图象位置与
a、b、c、 的
正负关系一、定义二、顶点与对称轴四、图象位置与
a、b、c、 的
正负关系一般地，如果
y=ax2+bx+c(a，b，c
是常数，a≠0)，那么，y
叫做x的二次函数。三、解析式的求法一、定义二、顶点与对称轴三、解析式的求法四、图象位置与
a、b、c、 的
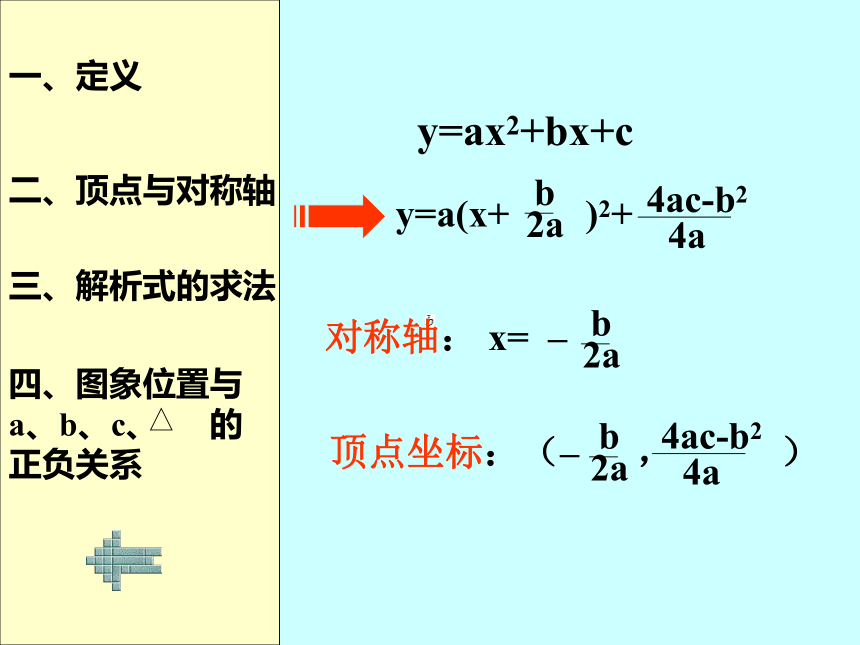
正负关系y=ax2+bx+c 对称轴： x= – 顶点坐标：（– ， ）一、定义二、顶点与对称轴三、解析式的求法四、图象位置与
a、b、c、 的
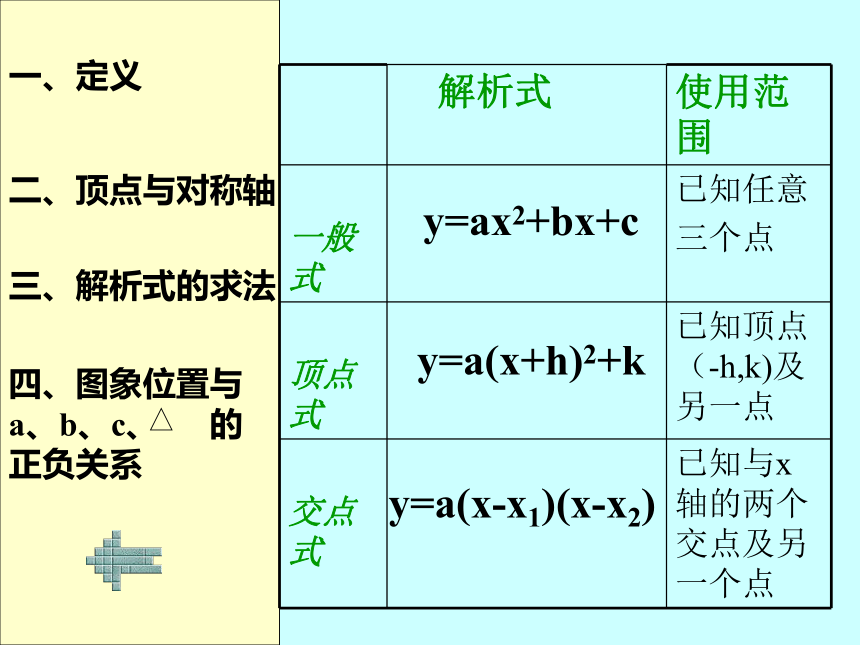
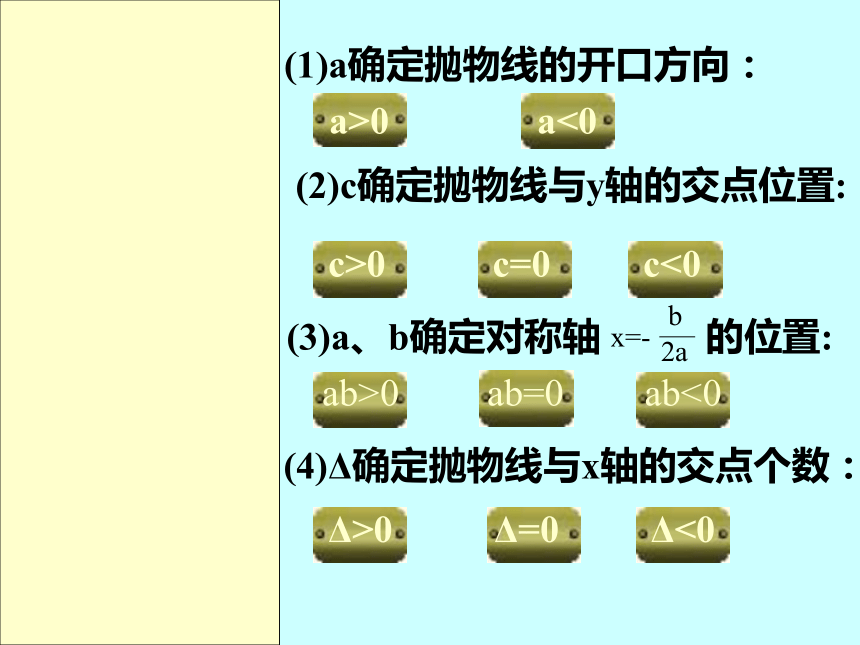
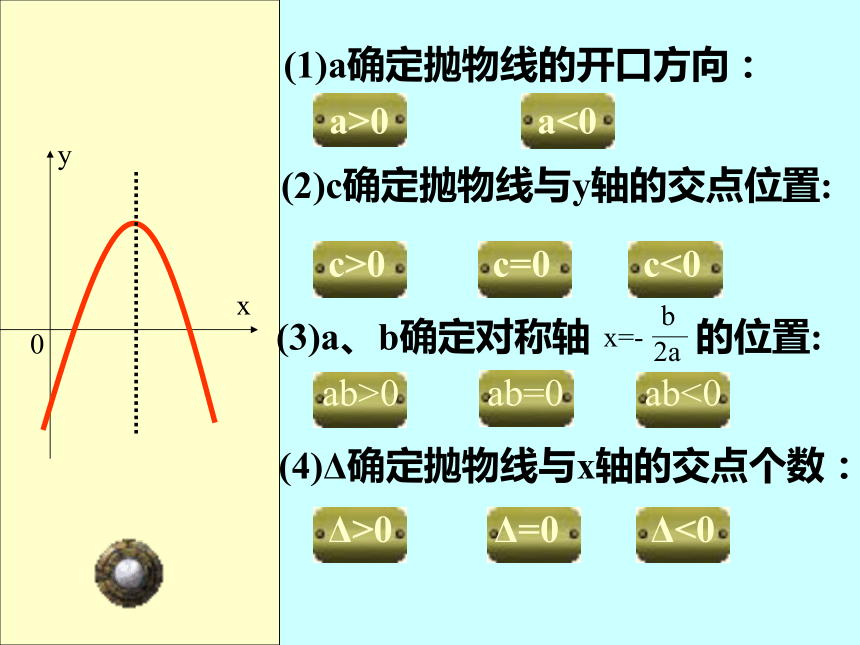
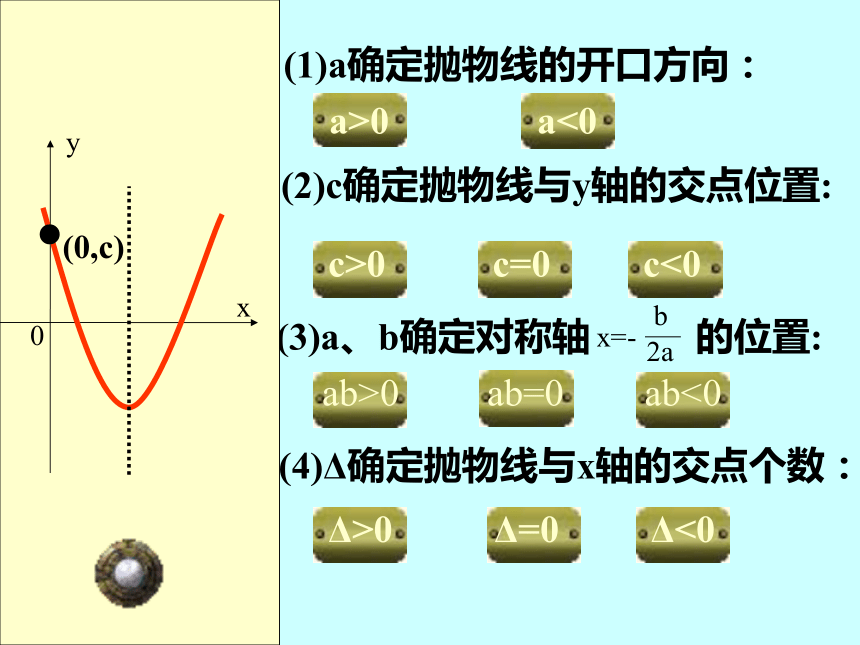
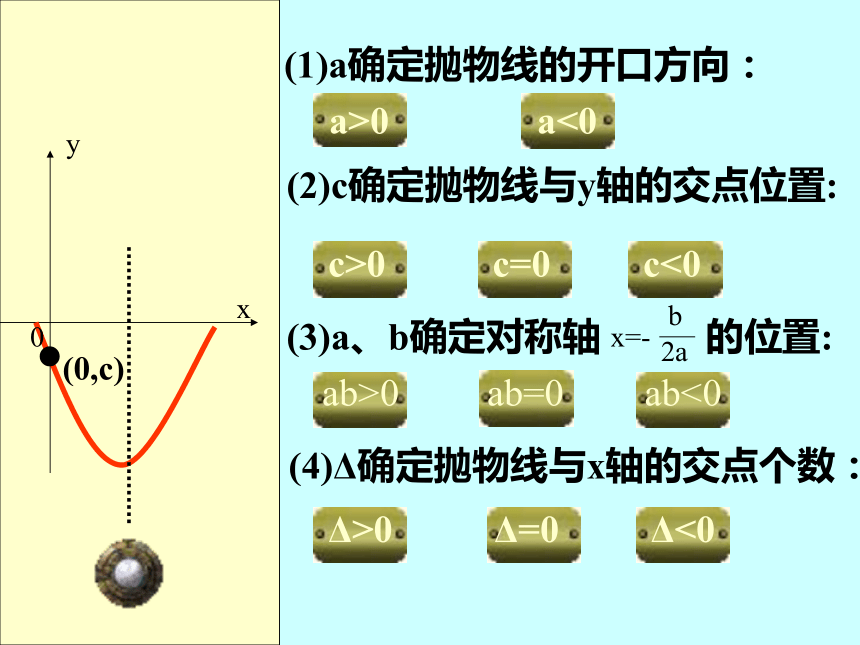
正负关系y=ax2+bx+cy=a(x+h)2+ky=a(x-x1)(x-x2) (1)a确定抛物线的开口方向：a>0a<0 (2)c确定抛物线与y轴的交点位置:c>0c=0c<0 (3)a、b确定对称轴 的位置:ab>0ab=0ab<0 (4)Δ确定抛物线与x轴的交点个数：Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数：xy0a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (2)c确定抛物线与y轴的交点位置:(3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数：a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数：xy0?(0,c)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数：xy0?(0,0)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数：xy0?(0,c)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数： xy0a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数：xy0a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数：xy0a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数：?(x1,0)?(x2,0)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数：xy0?(x,0)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 的位置: (4)Δ确定抛物线与x轴的交点个数：xy0?a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0例1： 已知二次函数y=—x2+x-—
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C，
A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大
（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？例1： 已知二次函数y=—x2+x-—
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C，
A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大
（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？解:解0xy(3)解0?M(-1,-2)??C(0,-–)??A(-3,0)B(1,0)3 2yxD解解0xx=-1??(0,-–)??(-3,0)(1,0)3 2:(5)?(-1,-2)当x=-1时，y有最小值为
y最小值=-2
当x＜-1时，y随x的增大
而减小;解:0?(-1,-2)??(0,-–)??(-3,0)(1,0)3 2yx由图象可知(6)返回巩固练习（1）二次函数y=x2-x-6的图象顶点坐标是___________对称轴是_________。
（2）抛物线y=-2x2+4x与x轴的交点坐标是___________
（3）已知函数y=—x2-x-4，当函数值y随x的增大而减小时，x的取值范围是___________
（4）二次函数y=mx2-3x+2m-m2的图象经过原点，则m= ____。12（0，0）（2，0）x<12返回如图，在△ABC中∠B=90o，AB=12cm，BC=24cm，动点P从A开始沿AB边以2cm/s的速度向B运动，动点Q从B开始沿BC边以4cm/s的速度向C运动，如果P、Q分别从A、B同时出发。
（1）写出△PBQ的面积S与运动时间t之间的函数关系式，并写出自变量t的取值范围；
（2）当t为何值时，△PBQ的面积S最大，最大值是多少？ 例2；BP=12-2t，BQ=4t
△PBQ的面积:
S=1/2(12-2t) ?4t
即S=- 4t2+24t=- 4(t-3)2+36
在⊙O的内接三角形ABC中，AB+AC=12，AD垂直于BC，垂足为D，且AD=3，设⊙O的半径为y，AB为x。
（1）求y与x的函数关系式；
（2）当AB长等于多少时，⊙O的面积最大？最大面积是多少？ 课时训练△ABE∽ △ADC
AB ?AC=AD ?AE
X ?(12-X)=2y ?3
y=-1/6x2+2X能力训练 二次函数的图象如图所示，则在下列各不等式
中成立的个数是____________1-10xy返回①abc<0
②a+b+c < 0
③a+c > b
④2a+b=0
⑤Δ=b-4ac > 0
归纳小结： （1）二次函数y=ax2+bx+c及抛物线的性质和应用
注意：图象的递增性，以及利用图象求自变量x或函
数值y的取值范围返回再见