26.1.1 反比例函数(课件)(共29张PPT)
文档属性
| 名称 | 26.1.1 反比例函数(课件)(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
反比例函数
1. 理解并掌握反比例函数的概念. (重点)
2. 从实际问题中抽象出反比例函数的概念,能根据已知条件确定反比例函数的解析式. (重点、难点)
1.什么是函数?什么是一次函数?什么是二次函数?
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是 x的函数.
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数. 特别的,当b=0时,y=kx为正比例函数.
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数.
2.已知登山队原来所在位置的温度为10℃,海拔每升高1km,气温下降6℃.若登山队又向上登高xkm,他们现在所在位置的温度为y℃,则y与x之间的函数解析式为___________.
3.若y=(k-1)x2+2是二次函数,则k的取值范围是_____.
y=-6x+10
k≠0
下列问题中,变量间具有函数关系吗?如果有,它们的解析式有什么共同特点?
(1) 京沪线铁路全程为1463km,某次列车的平均速度v(单位:km/h) 随此次列车的全程运行时间t(单位:h) 的变化而变化;
下列问题中,变量间具有函数关系吗?如果有,它们的解析式有什么共同特点?
(2) 某住宅小区要种植一块面积为1000m2的矩形草坪,草坪的长y(单位:m)随宽x(单位:m)的变化而变化;
下列问题中,变量间具有函数关系吗?如果有,它们的解析式有什么共同特点?
(3)已知北京市的总面积为1.68×104km2 ,人均占有面积S(km2/人) 随全市总人口n(单位:人)的变化而变化.
下列关系式中,变量间具有函数关系吗 如果有,它们的解析式有什么共同特点
上述解析式都具有 的形式,其中k是非零常数.
(k为常数,k≠0)的函数,叫做反比例函数,
一般地,形如
其中x是自变量,y是函数.
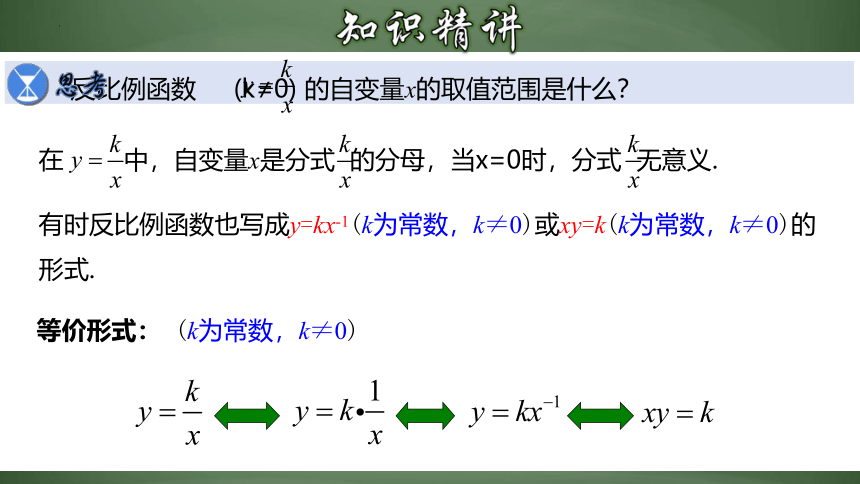
反比例函数 (k≠0) 的自变量x的取值范围是什么?
在 中,自变量x是分式 的分母,当x=0时,分式 无意义.
有时反比例函数也写成y=kx-1(k为常数,k≠0)或xy=k(k为常数,k≠0)的形式.
等价形式: (k为常数,k≠0)
下列哪些关系中的y是x的反比例函数?
,
y=6x+1 y=x2-1
xy=123
y=4x
√
√
例1.已知y是x的反比例函数,并且当x=2时,y=6.
(1) 写出y关于x的函数解析式;
(2) 当x=4时,求y的值.
分析:因为y是x的反比例函数,所以设 ,再把x=2和y=6代入上式就可以求出常数k的值.
解:(1)设 .
因为当x=2时,y=6,所以有 . 解得k=12
因此
(2)把x=4代入 ,得
已知y与x2成反比例,并且当x=3时,y=4.
(1)写出y关于x的函数解析式;
(2)求x=1.5时,求y的值;
(3)当y=6时,求x的值.
解:(1)设 ,因为当x=3时,y=4,所以有 . 解得k=36
因此 ;
(2)把x=1.5代入 ,得 ;
(3)当y=6时, ,解得 x= .
例2.当m取何值时,是关于x的反比例函数?
解:∵是关于x的反比例函数,
∴ ,
解得 ,
∴,
【点睛】已知某个函数为反比例函数,只需要根据反比例函数的定义列出方程(组)求解即可,如本题中x的次数为-1,且系数不等于0.
k为何值时,y=(k2+k)是反比例函数.
解 ∵函数y=(k2+k)是反比例函数,
∴
解得k=2.
故k为2时,y=(k2+k)是反比例函数.
例3.人的视觉机能受运动速度的影响很大,行驶中司机在驾驶室内观察前方物体是动态的,车速增加,视野变窄. 当车速为50km/h时,视野为80度,如果视野f(度) 是车速v(km/h) 的反比例函数,求f关于v的函数解析式,并计算当车速为100km/h 时视野的度数.
当v=100 时,f=40.
所以当车速为100km/h 时视野为40度.
解:设 . 由题意知,当v=50时,f=80,
解得k=4000.
因此
所以
例4.如图,某养鸡场利用一面长为11m的墙,其他三面用栅栏围成矩形,面积为,设与墙垂直的边长为xm,与墙平行的边长为ym.
(1)直接写出y与x的函数关系式为______;
(2)现有两种方案或,试选择合理的设计方案,并求此栅栏总长.
(1)解:根据题意得:,
∴y与x的函数关系式为:;
例4.如图,某养鸡场利用一面长为11m的墙,其他三面用栅栏围成矩形,面积为,设与墙垂直的边长为xm,与墙平行的边长为ym.
(2)现有两种方案或,试选择合理的设计方案,并求此栅栏总长.
(2)解:当x= 5时,,
∵,
∴不符合题意,舍去;
当x=6时,,
∵,
∴符合题意,此栅栏总长为:;
答:应选择x = 6的设计方案,此栅栏总长为22m.
如图所示,已知菱形ABCD的面积为180,设它的两条对角线AC,BD的长分别为x,y. 写出变量y与x之间的关系式,并指出它是什么函数.
A
B
C
D
解:因为菱形的面积等于两条对角线长乘积的一半,
所以
所以变量y与x之间的关系式为 ,
它是反比例函数.
1.下列函数是反比例函数的是( )
A. y=x B. y=kx-1 C.y=- D.y=
2.在函数y=-中,自变量x的取值范围是( )
A.x>0 B.x≠0 C.x<0 D.全体实数
3.已知一个函数满足下表(x为自变量):
则这个函数的解析式为( )
A.y= B.y=-C.y=D.y=-
C
B
B
4.某公司推出的一款新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动.一部售价为9330元的新手机,前期付款2000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数解析式是( )
A. y=+2000 B. y=-2000 C.y= D.y=
C
5.如果y是n的反比例函数,n是x的正比例函数,那么y是x的( )
A.反比例函数 B.正比例函数
C.一次函数 D.反比例函数或正比例函数
A
6.已知一个三角形的面积为1,一边长为x,这条边上的高为y,则y与x的函数解析式为_______.
7.在反比例函数y=-中,常数k=_____.
8.已知函数y=3xm-7是反比例函数,则m=____.
y=
-
6
9.当m=_____时,关于x的函数y=(m+1)x-2是反比例函数.
10.已知反比例函数y=,当x=2时,y=1,则k的值为_____.
11.已知y是x的反比例函数,当x的值由2增加到4时,y的值减小3,则这个反比例函数的解析式为______.
1
2
y=
12.用函数解析式表示下列问题中变量间的对应关系:
(1)一个游泳池的容积为2000m3,游泳池注满水所用时间t(单位:h)随注水速度v(单位:m3/h)的变化而变化;
(2)某长方体的体积为1000cm3,长方体的高h(单位:cm)随底面积S(单位:cm2)的变化而变化;
(3)一个物体重100N,物体对地面的压强p(单位:pa)随物体与地面的接触面积S(单位:m2)的变化而变化.
13.已知:,与成正比例,与成反比例.当时,;当时,.求与的函数解析式.
解:(1)设y1=k1(x+1)(k1≠0),y2=(k2≠0),
∴y=k1(x+1)+ .
∵当x=1时,y=7.当x=3时,y=4,
∴,
∴,
∴y关于x的函数解析式是:y=(x+1)+;
14.某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
(1)观察表中数据,x,y满足什么函数关系 请求出这个函数解析式;
(2)若商场计划每天的销售利润为3200元,则其单价应定为多少元
解:由表中数据得xy=6400
∴y是x的反比例函数,函数解析式为y=.
(1)观察表中数据,x,y满足什么函数关系 请求出这个函数解析式;
(2)若商场计划每天的销售利润为3200元,则其单价应定为多少元
解:由题意得(x-120)y=3200
(x-120)×6400=3200,
解得x=240
答:若商场计划每天的销售利润为3200元,则其单价应定为240元.
(k为常数,k≠0)的函数,叫做反比例函数,
一般地,形如
其中x是自变量,y是函数.
等价形式: (k为常数,k≠0)
反比例函数
1. 理解并掌握反比例函数的概念. (重点)
2. 从实际问题中抽象出反比例函数的概念,能根据已知条件确定反比例函数的解析式. (重点、难点)
1.什么是函数?什么是一次函数?什么是二次函数?
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是 x的函数.
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数. 特别的,当b=0时,y=kx为正比例函数.
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数.
2.已知登山队原来所在位置的温度为10℃,海拔每升高1km,气温下降6℃.若登山队又向上登高xkm,他们现在所在位置的温度为y℃,则y与x之间的函数解析式为___________.
3.若y=(k-1)x2+2是二次函数,则k的取值范围是_____.
y=-6x+10
k≠0
下列问题中,变量间具有函数关系吗?如果有,它们的解析式有什么共同特点?
(1) 京沪线铁路全程为1463km,某次列车的平均速度v(单位:km/h) 随此次列车的全程运行时间t(单位:h) 的变化而变化;
下列问题中,变量间具有函数关系吗?如果有,它们的解析式有什么共同特点?
(2) 某住宅小区要种植一块面积为1000m2的矩形草坪,草坪的长y(单位:m)随宽x(单位:m)的变化而变化;
下列问题中,变量间具有函数关系吗?如果有,它们的解析式有什么共同特点?
(3)已知北京市的总面积为1.68×104km2 ,人均占有面积S(km2/人) 随全市总人口n(单位:人)的变化而变化.
下列关系式中,变量间具有函数关系吗 如果有,它们的解析式有什么共同特点
上述解析式都具有 的形式,其中k是非零常数.
(k为常数,k≠0)的函数,叫做反比例函数,
一般地,形如
其中x是自变量,y是函数.
反比例函数 (k≠0) 的自变量x的取值范围是什么?
在 中,自变量x是分式 的分母,当x=0时,分式 无意义.
有时反比例函数也写成y=kx-1(k为常数,k≠0)或xy=k(k为常数,k≠0)的形式.
等价形式: (k为常数,k≠0)
下列哪些关系中的y是x的反比例函数?
,
y=6x+1 y=x2-1
xy=123
y=4x
√
√
例1.已知y是x的反比例函数,并且当x=2时,y=6.
(1) 写出y关于x的函数解析式;
(2) 当x=4时,求y的值.
分析:因为y是x的反比例函数,所以设 ,再把x=2和y=6代入上式就可以求出常数k的值.
解:(1)设 .
因为当x=2时,y=6,所以有 . 解得k=12
因此
(2)把x=4代入 ,得
已知y与x2成反比例,并且当x=3时,y=4.
(1)写出y关于x的函数解析式;
(2)求x=1.5时,求y的值;
(3)当y=6时,求x的值.
解:(1)设 ,因为当x=3时,y=4,所以有 . 解得k=36
因此 ;
(2)把x=1.5代入 ,得 ;
(3)当y=6时, ,解得 x= .
例2.当m取何值时,是关于x的反比例函数?
解:∵是关于x的反比例函数,
∴ ,
解得 ,
∴,
【点睛】已知某个函数为反比例函数,只需要根据反比例函数的定义列出方程(组)求解即可,如本题中x的次数为-1,且系数不等于0.
k为何值时,y=(k2+k)是反比例函数.
解 ∵函数y=(k2+k)是反比例函数,
∴
解得k=2.
故k为2时,y=(k2+k)是反比例函数.
例3.人的视觉机能受运动速度的影响很大,行驶中司机在驾驶室内观察前方物体是动态的,车速增加,视野变窄. 当车速为50km/h时,视野为80度,如果视野f(度) 是车速v(km/h) 的反比例函数,求f关于v的函数解析式,并计算当车速为100km/h 时视野的度数.
当v=100 时,f=40.
所以当车速为100km/h 时视野为40度.
解:设 . 由题意知,当v=50时,f=80,
解得k=4000.
因此
所以
例4.如图,某养鸡场利用一面长为11m的墙,其他三面用栅栏围成矩形,面积为,设与墙垂直的边长为xm,与墙平行的边长为ym.
(1)直接写出y与x的函数关系式为______;
(2)现有两种方案或,试选择合理的设计方案,并求此栅栏总长.
(1)解:根据题意得:,
∴y与x的函数关系式为:;
例4.如图,某养鸡场利用一面长为11m的墙,其他三面用栅栏围成矩形,面积为,设与墙垂直的边长为xm,与墙平行的边长为ym.
(2)现有两种方案或,试选择合理的设计方案,并求此栅栏总长.
(2)解:当x= 5时,,
∵,
∴不符合题意,舍去;
当x=6时,,
∵,
∴符合题意,此栅栏总长为:;
答:应选择x = 6的设计方案,此栅栏总长为22m.
如图所示,已知菱形ABCD的面积为180,设它的两条对角线AC,BD的长分别为x,y. 写出变量y与x之间的关系式,并指出它是什么函数.
A
B
C
D
解:因为菱形的面积等于两条对角线长乘积的一半,
所以
所以变量y与x之间的关系式为 ,
它是反比例函数.
1.下列函数是反比例函数的是( )
A. y=x B. y=kx-1 C.y=- D.y=
2.在函数y=-中,自变量x的取值范围是( )
A.x>0 B.x≠0 C.x<0 D.全体实数
3.已知一个函数满足下表(x为自变量):
则这个函数的解析式为( )
A.y= B.y=-C.y=D.y=-
C
B
B
4.某公司推出的一款新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动.一部售价为9330元的新手机,前期付款2000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数解析式是( )
A. y=+2000 B. y=-2000 C.y= D.y=
C
5.如果y是n的反比例函数,n是x的正比例函数,那么y是x的( )
A.反比例函数 B.正比例函数
C.一次函数 D.反比例函数或正比例函数
A
6.已知一个三角形的面积为1,一边长为x,这条边上的高为y,则y与x的函数解析式为_______.
7.在反比例函数y=-中,常数k=_____.
8.已知函数y=3xm-7是反比例函数,则m=____.
y=
-
6
9.当m=_____时,关于x的函数y=(m+1)x-2是反比例函数.
10.已知反比例函数y=,当x=2时,y=1,则k的值为_____.
11.已知y是x的反比例函数,当x的值由2增加到4时,y的值减小3,则这个反比例函数的解析式为______.
1
2
y=
12.用函数解析式表示下列问题中变量间的对应关系:
(1)一个游泳池的容积为2000m3,游泳池注满水所用时间t(单位:h)随注水速度v(单位:m3/h)的变化而变化;
(2)某长方体的体积为1000cm3,长方体的高h(单位:cm)随底面积S(单位:cm2)的变化而变化;
(3)一个物体重100N,物体对地面的压强p(单位:pa)随物体与地面的接触面积S(单位:m2)的变化而变化.
13.已知:,与成正比例,与成反比例.当时,;当时,.求与的函数解析式.
解:(1)设y1=k1(x+1)(k1≠0),y2=(k2≠0),
∴y=k1(x+1)+ .
∵当x=1时,y=7.当x=3时,y=4,
∴,
∴,
∴y关于x的函数解析式是:y=(x+1)+;
14.某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
(1)观察表中数据,x,y满足什么函数关系 请求出这个函数解析式;
(2)若商场计划每天的销售利润为3200元,则其单价应定为多少元
解:由表中数据得xy=6400
∴y是x的反比例函数,函数解析式为y=.
(1)观察表中数据,x,y满足什么函数关系 请求出这个函数解析式;
(2)若商场计划每天的销售利润为3200元,则其单价应定为多少元
解:由题意得(x-120)y=3200
(x-120)×6400=3200,
解得x=240
答:若商场计划每天的销售利润为3200元,则其单价应定为240元.
(k为常数,k≠0)的函数,叫做反比例函数,
一般地,形如
其中x是自变量,y是函数.
等价形式: (k为常数,k≠0)
