青岛版数学八年级上册 1.2怎样判定三角形全等第2课时 课件(共13张PPT)
文档属性
| 名称 | 青岛版数学八年级上册 1.2怎样判定三角形全等第2课时 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 526.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 00:00:00 | ||
图片预览



文档简介
(共13张PPT)
1.2 怎样判定三角形全等
第2课时
学习目标
1、通过画图、操作、实验、观察等数学活动,探索三角形全等的判定方法。
2、了解判定方法“ASA、AAS”,能初步运用它们 判定两个三角形全等。
3、在动手操作的过程中,培养主动探索精神与合作交流意识。
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
实验与探究
问题1:
剪下你画出的三角形,与其他同学剪得的三角形(按同一条件)进行比较,这些三角形能重合吗?
(你也可以改变∠ ,∠ 的大小(∠ +∠ < 1800 )或改变线段a的长短)
答:两角及其夹边(角边角)
两角及其一角的对边(角角边)。
问题2:
做一做:已知:∠ = 700、∠ = 500、a = 10厘米。在硬纸片上画出⊿ABC,使∠B = ∠ 、∠C = ∠ 、BC = a。
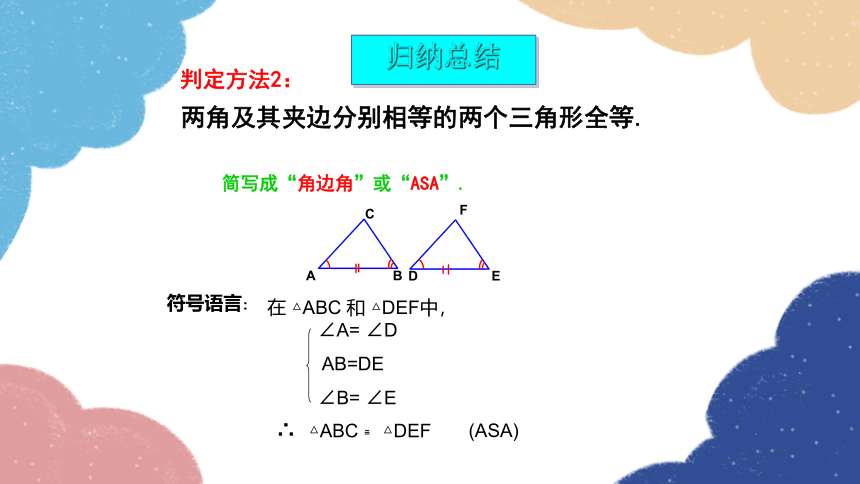
两角及其夹边分别相等的两个三角形全等.
简写成“角边角”或“ASA”.
判定方法2:
A
B
C
F
E
D
符号语言:
在 △ABC 和 △DEF中,
∠A= ∠D
AB=DE
∠B= ∠E
∴
△ABC ≌ △DEF
(ASA)
归纳总结
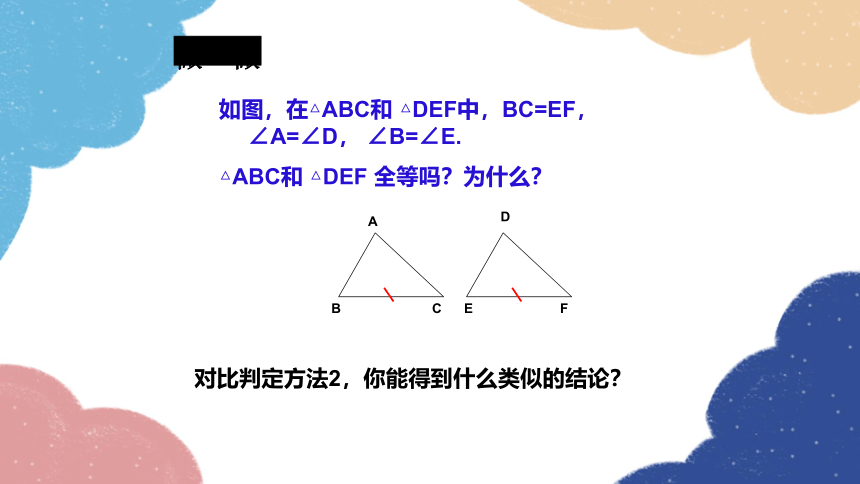
如图,在△ABC和 △DEF中,BC=EF,∠A=∠D, ∠B=∠E.
△ABC和 △DEF 全等吗?为什么?
A
B
C
D
E
F
做一做
对比判定方法2,你能得到什么类似的结论?
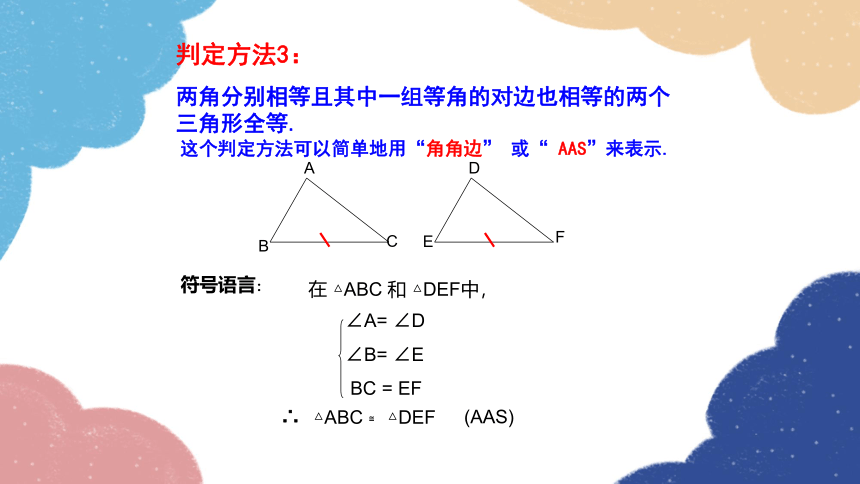
在 △ABC 和 △DEF中,
符号语言:
∠A= ∠D
∠B= ∠E
BC = EF
∴
△ABC ≌ △DEF
(AAS)
A
B
C
D
E
F
判定方法3:
两角分别相等且其中一组等角的对边也相等的两个三角形全等.
这个判定方法可以简单地用“角角边” 或“ AAS”来表示.
2、如图(2),∠A= ∠D, ,∠1= ∠2,要使△ABC ≌ △DEF ,还需添加的一个条件是 (答案不唯一)
①
②
③
图(1)
1、某同学把一块三角形的玻璃打破成三块,如图(1),现需配制一块同样大小的三角形玻璃,为了方便起见,只带上 块即可,根据是 。
学以致用
C
1
B
A
F
D
E
2
图(2)
③
ASA
思路
已知两角
找夹边(ASA)
找对边(AAS)
变式:如图,已知∠CAB=∠DAB,请你添加一个条件 ,
使得△ABC≌△ABD.
B
A
C
D
思路
已知一边一角
形成夹边的另一角(ASA)
与边相对的另一角(AAS)
隐含条件:AB=AB
形成夹角的另一边( SAS)
D
A
E
C
F
B
例3、如图,已知∠ACB=∠DFE,∠B=∠E,BC=EF,那么△ABC与△DEF全等吗?为什么
证明线段相等
三角形全等
线段中点定义
线段垂直平分的性质
角平分线的性质
等腰三角形的性质
…
如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢 ?
拓展提升
解:连结AC
∵AB∥CD,AD∥BC
∴∠BAC=∠DCA, ∠BCA=∠DAC.(两直 线平行,内错角相等)
在△ABC和△CDA中
A
B
D
C
∠BAC=∠DCA
AC=CA
∠BCA=∠DAC
∴
△ABC ≌ △CDA (ASA)
∴
AB=CD, AD=CB (全等三角形的对应边相等)
辅助线
转化
谈谈本节课你有哪些收获?
(知识,数学思想)
课堂小结
布置作业:
必做题:习题1.2的3、4、5.
选做题:习题1.2的8题。
1.2 怎样判定三角形全等
第2课时
学习目标
1、通过画图、操作、实验、观察等数学活动,探索三角形全等的判定方法。
2、了解判定方法“ASA、AAS”,能初步运用它们 判定两个三角形全等。
3、在动手操作的过程中,培养主动探索精神与合作交流意识。
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
实验与探究
问题1:
剪下你画出的三角形,与其他同学剪得的三角形(按同一条件)进行比较,这些三角形能重合吗?
(你也可以改变∠ ,∠ 的大小(∠ +∠ < 1800 )或改变线段a的长短)
答:两角及其夹边(角边角)
两角及其一角的对边(角角边)。
问题2:
做一做:已知:∠ = 700、∠ = 500、a = 10厘米。在硬纸片上画出⊿ABC,使∠B = ∠ 、∠C = ∠ 、BC = a。
两角及其夹边分别相等的两个三角形全等.
简写成“角边角”或“ASA”.
判定方法2:
A
B
C
F
E
D
符号语言:
在 △ABC 和 △DEF中,
∠A= ∠D
AB=DE
∠B= ∠E
∴
△ABC ≌ △DEF
(ASA)
归纳总结
如图,在△ABC和 △DEF中,BC=EF,∠A=∠D, ∠B=∠E.
△ABC和 △DEF 全等吗?为什么?
A
B
C
D
E
F
做一做
对比判定方法2,你能得到什么类似的结论?
在 △ABC 和 △DEF中,
符号语言:
∠A= ∠D
∠B= ∠E
BC = EF
∴
△ABC ≌ △DEF
(AAS)
A
B
C
D
E
F
判定方法3:
两角分别相等且其中一组等角的对边也相等的两个三角形全等.
这个判定方法可以简单地用“角角边” 或“ AAS”来表示.
2、如图(2),∠A= ∠D, ,∠1= ∠2,要使△ABC ≌ △DEF ,还需添加的一个条件是 (答案不唯一)
①
②
③
图(1)
1、某同学把一块三角形的玻璃打破成三块,如图(1),现需配制一块同样大小的三角形玻璃,为了方便起见,只带上 块即可,根据是 。
学以致用
C
1
B
A
F
D
E
2
图(2)
③
ASA
思路
已知两角
找夹边(ASA)
找对边(AAS)
变式:如图,已知∠CAB=∠DAB,请你添加一个条件 ,
使得△ABC≌△ABD.
B
A
C
D
思路
已知一边一角
形成夹边的另一角(ASA)
与边相对的另一角(AAS)
隐含条件:AB=AB
形成夹角的另一边( SAS)
D
A
E
C
F
B
例3、如图,已知∠ACB=∠DFE,∠B=∠E,BC=EF,那么△ABC与△DEF全等吗?为什么
证明线段相等
三角形全等
线段中点定义
线段垂直平分的性质
角平分线的性质
等腰三角形的性质
…
如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢 ?
拓展提升
解:连结AC
∵AB∥CD,AD∥BC
∴∠BAC=∠DCA, ∠BCA=∠DAC.(两直 线平行,内错角相等)
在△ABC和△CDA中
A
B
D
C
∠BAC=∠DCA
AC=CA
∠BCA=∠DAC
∴
△ABC ≌ △CDA (ASA)
∴
AB=CD, AD=CB (全等三角形的对应边相等)
辅助线
转化
谈谈本节课你有哪些收获?
(知识,数学思想)
课堂小结
布置作业:
必做题:习题1.2的3、4、5.
选做题:习题1.2的8题。
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
