15.2 线段的垂直平分线 (2) 课件(共25张PPT)
文档属性
| 名称 | 15.2 线段的垂直平分线 (2) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 951.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
沪科版 八年级上册
15.2 线段的垂直平分线 (2)
教学目标
能够利用尺规作图法作一条已知线段的垂直平分线,并尝试证明它的正确性.通过例题,理解三线交一点的意义.
教学重点:线段垂直平分线的判定定理
教学难点:三线交一点的理解与证明.
线段垂直平分线上的点与这条线段两个端点的距离相等.
与线段两个端点距离相等的点在这条线段的垂直平分线上.
线段垂直平分线的性质是解决线段相等问题的重要方法.
线段垂直平分线的判定可用来证明两线的垂直关系.
复习旧知
1.线段垂直平分线的性质定理
2.线段垂直平分线的判定定理
1.不能判定直线MN是线段AB的垂直平分线
的是( ).
A.MA=MB,NA=NB
B.AM=BM,MN⊥AB
C.MA=NA,MB=NB
D.MA=MB,MN平分AB且点M不在AB上
C
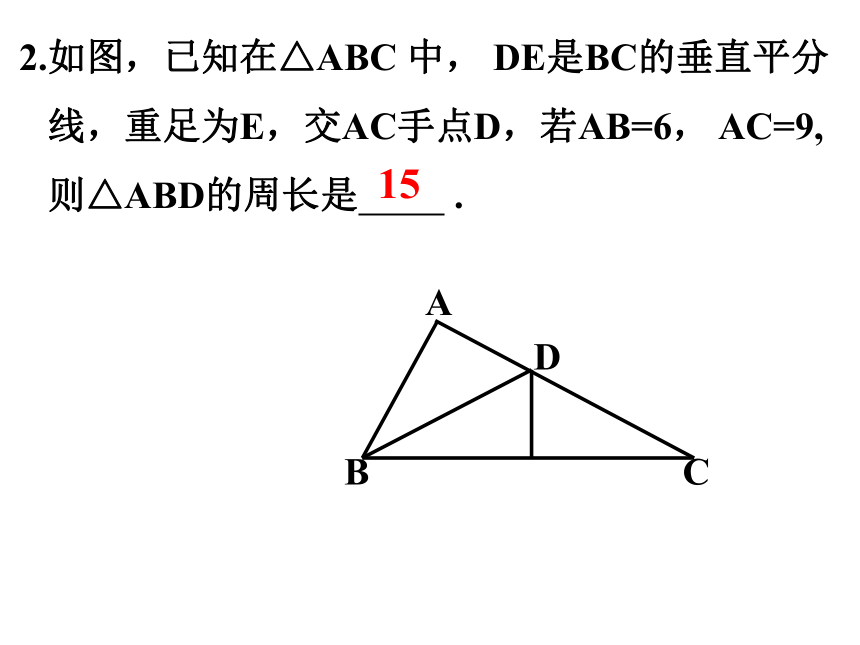
2.如图,已知在△ABC 中, DE是BC的垂直平分
线,重足为E,交AC手点D,若AB=6, AC=9,
则△ABD的周长是 .
A
B
C
D
15
A
B
C
D
E
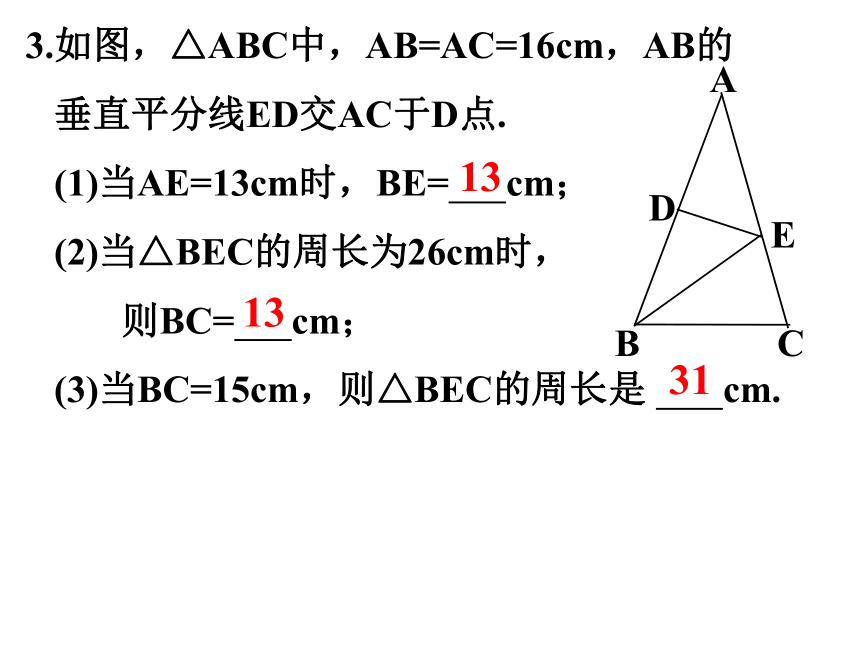
3.如图,△ABC中,AB=AC=16cm,AB的
垂直平分线ED交AC于D点.
(1)当AE=13cm时,BE= cm;
(2)当△BEC的周长为26cm时,
则BC= cm;
(3)当BC=15cm,则△BEC的周长是 cm.
13
13
31
A
B
C
Q
N
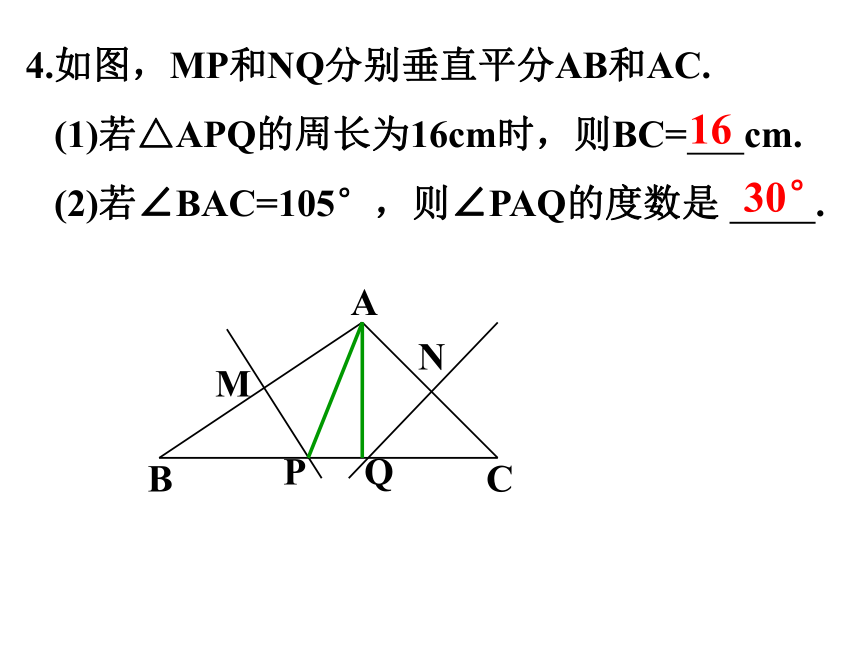
4.如图,MP和NQ分别垂直平分AB和AC.
(1)若△APQ的周长为16cm时,则BC= cm.
(2)若∠BAC=105°,则∠PAQ的度数是 .
P
M
16
30°
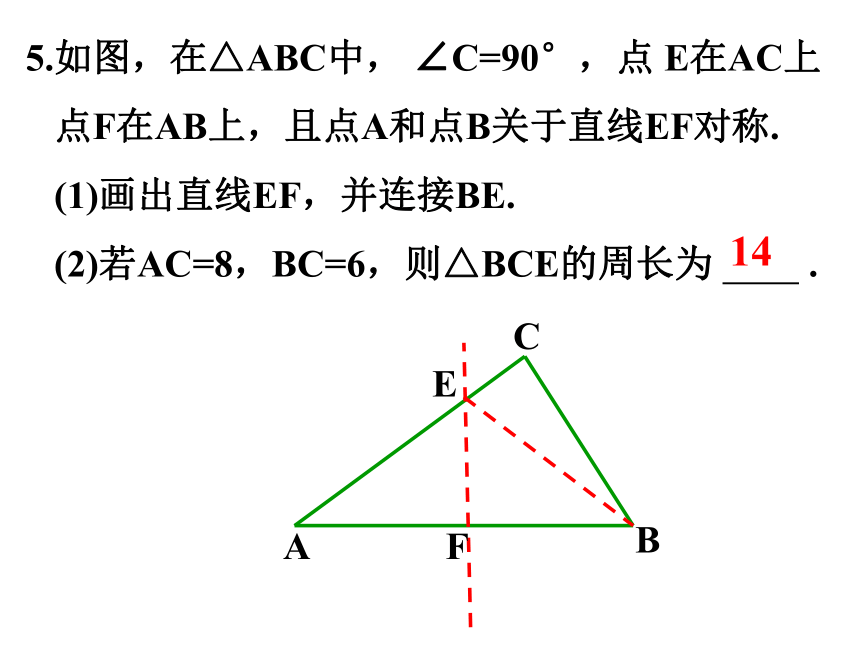
5.如图,在△ABC中, ∠C=90°,点 E在AC上
点F在AB上,且点A和点B关于直线EF对称.
(1)画出直线EF,并连接BE.
(2)若AC=8,BC=6,则△BCE的周长为 .
B
A
C
E
F
14
1.如果我们感觉两个平面图形是成轴对称的,你准备用什么方法去验证
2.两个成轴对称的图形,不经过折叠,你用什么方法作出它的对称轴
(1)将图形对折;
(2)用尺规作对应点所连线段的垂直平分线.
(1)用刻度尺先取一对对称点连线
的中点,然后作垂线.
(2)作出它的对称轴。
学习新知
如图,已知线段AB,用直尺和圆规作AB 的垂直平分线.
A
B
如图,已知线段AB,用直尺和圆规作AB 的垂直平分线.
A
B
C
D
你还有其他的方法作一条线段的垂直平分线吗
(1)分别以点A、B为圆心,
以大于 AB的长
为半径作弧,两弧相交
于C、D两点;
CD即为所求的直线.
(2) 作直线CD.
1
2
练习:见教材第63页例2.
(2)分别以点A、B为圆心,
以大于 AB的长
为半径作弧,两弧相交
于C、D两点;
CD即为所求的直线.
(3) 作直线CD.
1
2
A
B
(1) 连接AB.
C
D
如图,点A和点B关于某条直线成轴对称,
你能作出这条直线吗?
如图,已知,C,D是线段AB外两点,且CA=CB,DA=DB,求证:直线CD垂直平分线段AB
C
D
B
A
∵ CA=CB,
∴点C在AB的垂直平分线上.
∵ DA=DB,
∴点D在AB的垂直平分线上.
∴CD是AB的垂直平分线.
(两点确定一直线)
已知:如图, △ABC 的边AB,AC的垂直平分线相交于点P.
求证:点P在BC的垂直平分线上.
C
A
B
P
证明:
连接PA,PB,PC.
∵点P在AB的垂直平分线上,
∴PA=PB.
∵点P在AC的垂直平分线上,
∴PA=PC.
∴PB=PC.
∴点P在BC的垂直平分线上.
已知:如图, △PAC 的边AB,AC的垂直平分线相交于点PB.
求证:点P在BC的垂直平分线上.
C
A
B
P
证明:
连接PA,PB,PC.
∵点P在AB的垂直平分线上,
∴PA=PB.
∵点P在AC的垂直平分线上,
∴PA=PC.
∴PB=PC.
∴点P在BC的垂直平分线上.
三角形三边的垂直平分线相交于一点,
这点到三角形三个顶点的距离相等.
1.尺规作图: 在△ABC 中,作边AB的垂直平分线,
交AC于点M.(不写作法,保留作图痕迹)
练习巩固
C
A
B
M
E
F
EF为所求的直线.
2.如图,在△ABC 中,已知AB < BC< CA.
(1)尺规作图: 作边AB的垂直平分线PQ,交AC
于点P,交AB于点Q.(不写作法,保留作图痕迹)
A
B
C
P
(2)连接PB.若AC=6,BC=4,
则△PBC的周长为 .
10
Q
A村
B村
C村
3.为了推进农村新型合作医疗制度改革,准备在
某镇新建一个医疗点P,使点P到该镇所属A村、
B村、C村的村委会所在地的距离都相等(A,B,C
不在同一直线上,地理位置如图),请你用尺规
作图的方法确定点P的位置.不写作法,保留作图
痕迹.
P
图中的点P就是所要求作的点.
课堂小结
本节课你学到了什么
1.线段垂直平分线的作法.
2.作成轴对称的图形的对称轴的几种常见方法:
3.有许多图形的对称轴不止一条.
(1) 将图形对折;
(3)用尺规作对应点所连线段的垂直平分线.
(2)用刻度尺先取一对对称点连线的中点,
然后作垂线.
平面内到不在同一条直线的三个点A、B、C的距离相等的点有( ).
A.0个 B.1个 C.2个 D.3个
巩固新知
B
2.在△ ABC内一点P满足PA=PB=PC,则点P
一定是△ABC( ).
A.三条角平分线的交点
B.三边垂直平分线的交点
C.三条高的交点
D.三条中线的交点
B
A.65° B.60° C.55° D.45°
3.如图,在△ABC中, ∠B=55, ∠C=30°,分
别以点A和点C为圆心,大于 AC的长为半径
画弧, 两弧相交于点M、N,作直线MN,交
BC于点D,连结AD,则∠BAD的度数为( ).
1
2
A
A
B
C
D
4.如图,在口ABCD中,BD是它的一条对角线.
(1)尺规作图:
作BD的垂直平分线 EF,分别交 AD,BC于
点E,F(不写作法,保留作图痕迹);
(2)连接BE,若∠DBE=25°,
则∠AEB的度数为 .
A
D
B
C
E
F
65°
今天作业
课本P131页第3、4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
15.2 线段的垂直平分线 (2)
教学目标
能够利用尺规作图法作一条已知线段的垂直平分线,并尝试证明它的正确性.通过例题,理解三线交一点的意义.
教学重点:线段垂直平分线的判定定理
教学难点:三线交一点的理解与证明.
线段垂直平分线上的点与这条线段两个端点的距离相等.
与线段两个端点距离相等的点在这条线段的垂直平分线上.
线段垂直平分线的性质是解决线段相等问题的重要方法.
线段垂直平分线的判定可用来证明两线的垂直关系.
复习旧知
1.线段垂直平分线的性质定理
2.线段垂直平分线的判定定理
1.不能判定直线MN是线段AB的垂直平分线
的是( ).
A.MA=MB,NA=NB
B.AM=BM,MN⊥AB
C.MA=NA,MB=NB
D.MA=MB,MN平分AB且点M不在AB上
C
2.如图,已知在△ABC 中, DE是BC的垂直平分
线,重足为E,交AC手点D,若AB=6, AC=9,
则△ABD的周长是 .
A
B
C
D
15
A
B
C
D
E
3.如图,△ABC中,AB=AC=16cm,AB的
垂直平分线ED交AC于D点.
(1)当AE=13cm时,BE= cm;
(2)当△BEC的周长为26cm时,
则BC= cm;
(3)当BC=15cm,则△BEC的周长是 cm.
13
13
31
A
B
C
Q
N
4.如图,MP和NQ分别垂直平分AB和AC.
(1)若△APQ的周长为16cm时,则BC= cm.
(2)若∠BAC=105°,则∠PAQ的度数是 .
P
M
16
30°
5.如图,在△ABC中, ∠C=90°,点 E在AC上
点F在AB上,且点A和点B关于直线EF对称.
(1)画出直线EF,并连接BE.
(2)若AC=8,BC=6,则△BCE的周长为 .
B
A
C
E
F
14
1.如果我们感觉两个平面图形是成轴对称的,你准备用什么方法去验证
2.两个成轴对称的图形,不经过折叠,你用什么方法作出它的对称轴
(1)将图形对折;
(2)用尺规作对应点所连线段的垂直平分线.
(1)用刻度尺先取一对对称点连线
的中点,然后作垂线.
(2)作出它的对称轴。
学习新知
如图,已知线段AB,用直尺和圆规作AB 的垂直平分线.
A
B
如图,已知线段AB,用直尺和圆规作AB 的垂直平分线.
A
B
C
D
你还有其他的方法作一条线段的垂直平分线吗
(1)分别以点A、B为圆心,
以大于 AB的长
为半径作弧,两弧相交
于C、D两点;
CD即为所求的直线.
(2) 作直线CD.
1
2
练习:见教材第63页例2.
(2)分别以点A、B为圆心,
以大于 AB的长
为半径作弧,两弧相交
于C、D两点;
CD即为所求的直线.
(3) 作直线CD.
1
2
A
B
(1) 连接AB.
C
D
如图,点A和点B关于某条直线成轴对称,
你能作出这条直线吗?
如图,已知,C,D是线段AB外两点,且CA=CB,DA=DB,求证:直线CD垂直平分线段AB
C
D
B
A
∵ CA=CB,
∴点C在AB的垂直平分线上.
∵ DA=DB,
∴点D在AB的垂直平分线上.
∴CD是AB的垂直平分线.
(两点确定一直线)
已知:如图, △ABC 的边AB,AC的垂直平分线相交于点P.
求证:点P在BC的垂直平分线上.
C
A
B
P
证明:
连接PA,PB,PC.
∵点P在AB的垂直平分线上,
∴PA=PB.
∵点P在AC的垂直平分线上,
∴PA=PC.
∴PB=PC.
∴点P在BC的垂直平分线上.
已知:如图, △PAC 的边AB,AC的垂直平分线相交于点PB.
求证:点P在BC的垂直平分线上.
C
A
B
P
证明:
连接PA,PB,PC.
∵点P在AB的垂直平分线上,
∴PA=PB.
∵点P在AC的垂直平分线上,
∴PA=PC.
∴PB=PC.
∴点P在BC的垂直平分线上.
三角形三边的垂直平分线相交于一点,
这点到三角形三个顶点的距离相等.
1.尺规作图: 在△ABC 中,作边AB的垂直平分线,
交AC于点M.(不写作法,保留作图痕迹)
练习巩固
C
A
B
M
E
F
EF为所求的直线.
2.如图,在△ABC 中,已知AB < BC< CA.
(1)尺规作图: 作边AB的垂直平分线PQ,交AC
于点P,交AB于点Q.(不写作法,保留作图痕迹)
A
B
C
P
(2)连接PB.若AC=6,BC=4,
则△PBC的周长为 .
10
Q
A村
B村
C村
3.为了推进农村新型合作医疗制度改革,准备在
某镇新建一个医疗点P,使点P到该镇所属A村、
B村、C村的村委会所在地的距离都相等(A,B,C
不在同一直线上,地理位置如图),请你用尺规
作图的方法确定点P的位置.不写作法,保留作图
痕迹.
P
图中的点P就是所要求作的点.
课堂小结
本节课你学到了什么
1.线段垂直平分线的作法.
2.作成轴对称的图形的对称轴的几种常见方法:
3.有许多图形的对称轴不止一条.
(1) 将图形对折;
(3)用尺规作对应点所连线段的垂直平分线.
(2)用刻度尺先取一对对称点连线的中点,
然后作垂线.
平面内到不在同一条直线的三个点A、B、C的距离相等的点有( ).
A.0个 B.1个 C.2个 D.3个
巩固新知
B
2.在△ ABC内一点P满足PA=PB=PC,则点P
一定是△ABC( ).
A.三条角平分线的交点
B.三边垂直平分线的交点
C.三条高的交点
D.三条中线的交点
B
A.65° B.60° C.55° D.45°
3.如图,在△ABC中, ∠B=55, ∠C=30°,分
别以点A和点C为圆心,大于 AC的长为半径
画弧, 两弧相交于点M、N,作直线MN,交
BC于点D,连结AD,则∠BAD的度数为( ).
1
2
A
A
B
C
D
4.如图,在口ABCD中,BD是它的一条对角线.
(1)尺规作图:
作BD的垂直平分线 EF,分别交 AD,BC于
点E,F(不写作法,保留作图痕迹);
(2)连接BE,若∠DBE=25°,
则∠AEB的度数为 .
A
D
B
C
E
F
65°
今天作业
课本P131页第3、4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
