人教A版(2019)高中数学选择性必修第一册 1.4 《用空间向量研究直线、平面的位置关系》名师课件(共34张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 1.4 《用空间向量研究直线、平面的位置关系》名师课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 11:21:45 | ||
图片预览





文档简介
(共34张PPT)
人教A版同步教材名师课件
用空间向量研究直线、平面的位置关系
学习目标
学 习 目 标 核心素养
空间中点、直线和平面的向量表示 直观想象
数学抽象
空间中直线、平面的平行 直观想象
逻辑推理
空间中直线、平面的垂直 直观想象
逻辑推理
学习目标
学习目标:
1.了解空间中点、直线和平面的向量表示.
2.掌握直线的方向向量,平面的法向量的概念及求法.
3.熟练掌握用方向向量,法向量证明线线、线面、面面间的平行关系.
4.能利用平面法向量证明线面和面面垂直.
5.能利用直线的方向向量和平面的法向量判定并证明空间中的垂直关系.
学科核心素养:
1.通过空间中点、直线和平面的向量表示的学习,培养学生直观想象和逻辑推理的核心素养.
2.通过直线的方向向量和平面法向量的学习,培养学生数学运算的核心素养.
3.借助利用空间向量解决平行问题的学习,提升学生的数学运算及逻辑推理的核心素养.
4.借助空间向量证明线面垂直和面面垂直的学习,提升学生的数学运算和逻辑推理核心素养.
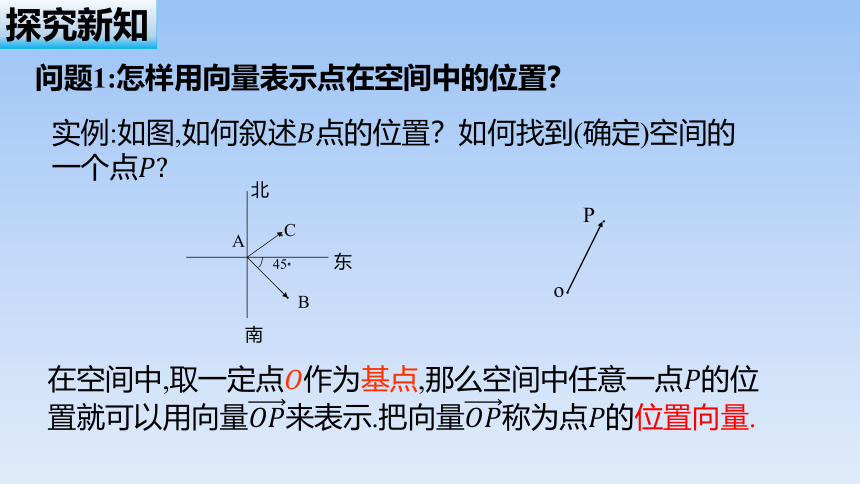
在空间中,取一定点作为基点,那么空间中任意一点的位置就可以用向量来表示.把向量称为点的位置向量.
P
·
o
·
问题1:怎样用向量表示点在空间中的位置?
东
南
A
45。
.C
北
实例:如图,如何叙述点的位置?如何找到(确定)空间的一个点
.
B
探究新知
问题2:在空间给定一个定点和一个定方向(向量),能确定一条直线在空间中的位置吗
我们把向量叫直线的方向向量,若仅研究两直线平行、垂直、成角时,可以用向量代替直线吗 直线的方向向量有多少个,为方便,我们一般怎样取出直线的方向向量
探究新知
O
A
l
P
探究新知
如图,为经过已知点A且平行于已知非零向量的直线,对空间任意一点O,点P在直线上的充要条件是
存在实数t,使,其中向量叫做直线的方向向量.
,
①和②都称为空间直线的向量表示式,空间任意直线由空间一点及直线的方向向量惟一决定.
由此可判断空间任意三点是否共线.
·
o
b
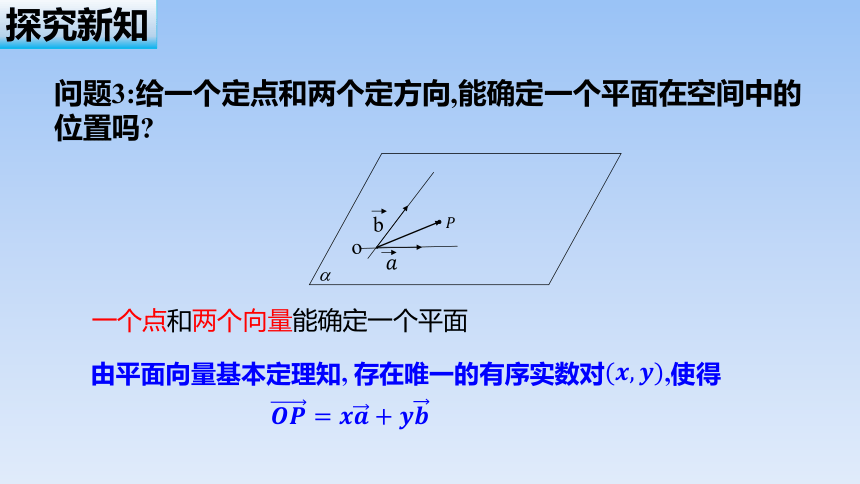
一个点和两个向量能确定一个平面
问题3:给一个定点和两个定方向,能确定一个平面在空间中的位置吗
探究新知
由平面向量基本定理知, 存在唯一的有序实数对,使得
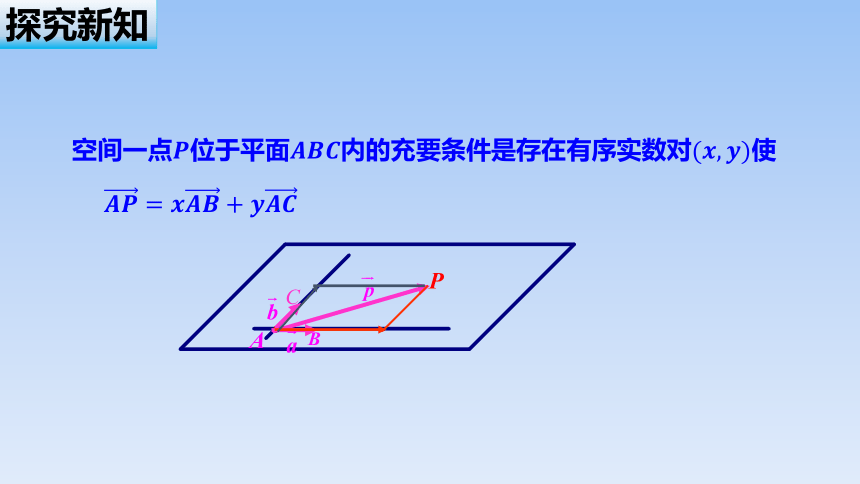
空间一点位于平面内的充要条件是存在有序实数对使
C
探究新知
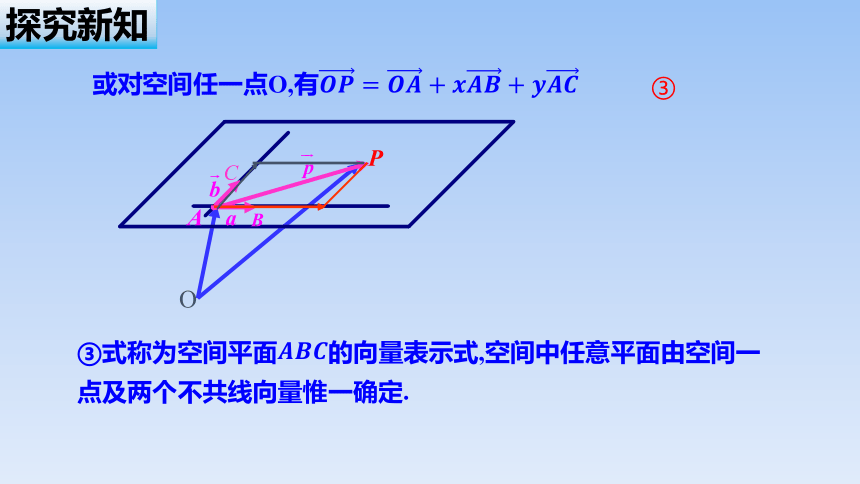
或对空间任一点O,有
C
③
③式称为空间平面的向量表示式,空间中任意平面由空间一点及两个不共线向量惟一确定.
O
探究新知
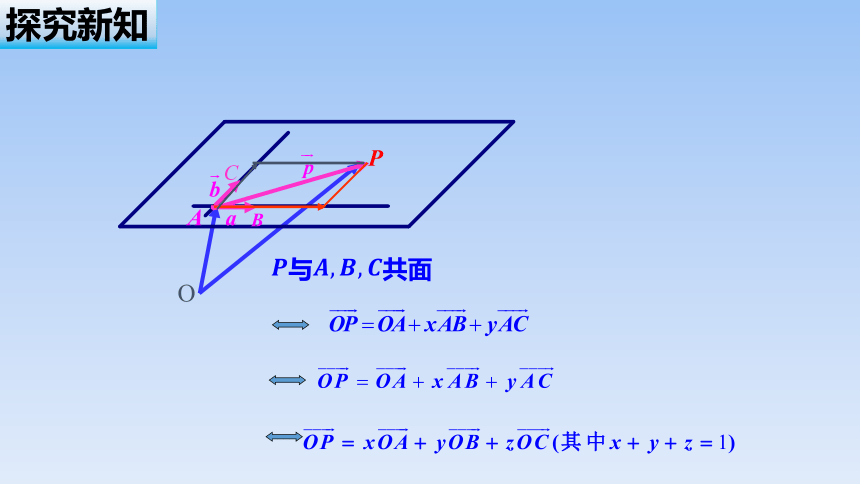
C
O
与共面
探究新知
探究新知
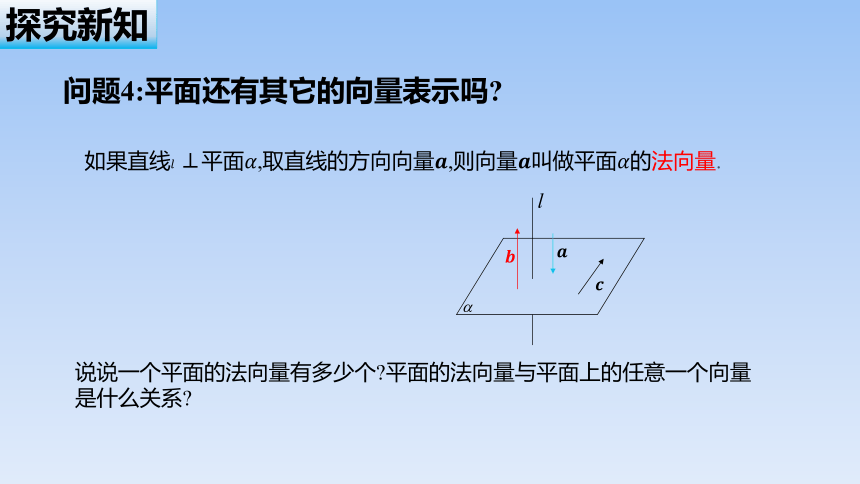
如图,直线.取直线的方向向量我们称向量为平面的法向量(normal vector).给定一个点和一个向量,那么过点且以向量为法向量的平面完全确定,可以表示为集合.
说说一个平面的法向量有多少个 平面的法向量与平面上的任意一个向量是什么关系
问题4:平面还有其它的向量表示吗
如果直线 ⊥平面,取直线的方向向量,则向量叫做平面的法向量.
探究新知
·
一个定点和平面的一个法向量,确定一个平面.若仅仅研究两平面平行、垂直、成角时,可以用平面的法向量代替吗
给定一个定点和一个平面的法向量,能确定一个平面在空间中的位置吗
探究新知
l
l⊥α u∥v u=λv
a1=λa2,b1=λb2,c1=λc2 (λ∈R).
l
探究新知
思考:设平面外的直线的方向向量是=(a1,b1,c1),平面的法向量是=(a2,b2,c2),若//,则向量和向量有什么关系?
若 ⊥,则向量和向量有什么关系?
l∥α ⊥ ·=0 a1a2+b1b2+c1c2=0.
设直线的方向向量分别为=(a1,b1,c1), =(a2,b2,c2),
l⊥m ·=0 a1b1+a2b2+a3b3=0
l∥m ∥ a=λ a1=λa2,b1=λb2,c1=λc2(λ∈R).
线线的关系
探究新知
设直线l的方向向量为=(a1,b1,c1),平面α的法向量为=(a2,b2,c2),则
l⊥α ∥ =λ a1=λa2,b1=λb2,c1=λc2(λ∈R).
线面的关系
l∥α ⊥ ·=0 a1a2+b1b2+c1c2=0.
探究新知
设平面的法向量分别为=(a1,b1,c1),=(a2,b2,c2),
⊥ ⊥ ·=0 a1a2+b1b2+c1c2=0.
面面的关系
∥ ∥ =λ a1=λa2,b1=λb2,c1=λc2(λ∈R).
探究新知
例1、已知A(1,0,1)、B(0,1,1)、C(1,1,0),求平面ABC的一个法向量.
典例讲解
设平面ABC的法向量为=(x,y,z),
由题意知=(-1,1,0), =(1,0,-1).
因为⊥且⊥,所以
令x=1,得y=z=1.
所以平面ABC的一个法向量为=(1,1,1).
解析
利用待定系数法求平面法向量的步骤
方法归纳
(1)设向量:设平面的法向量为=(x,y,z).
(2)选向量:在平面内选取两不共线向量.
(3)列方程组:由列出方程组.
(4)解方程组:
(5)赋非零值:取其中一个为非零值(常取±1).
(6)得结论:得到平面的一个法向量.
变式训练
1.如图所示,在四棱锥中,底面是直角梯形,,底面,且,建立适当的空间直角坐标系,分别求平面与平面的一个法向量.
如图,以为原点,以,分别为轴的正方向建立空间直角坐标系,则则
易知向量是平面的一个法向量.
解析
变式训练
1.如图所示,在四棱锥中,底面是直角梯形,,底面,且,建立适当的空间直角坐标系,分别求平面与平面的一个法向量.
解析
设=(x,y,z)为平面SDC的法向量,
则即
取x=2,则y=-1,z=1,
所以平面SDC的一个法向量为(2,-1,1).
例2、已知正方体ABCD -A1B1C1D1的棱长为2,E、F分别是BB1、DD1的中点,求证:FC1∥平面ADE.
则有D(0,0,0),A(2,0,0),C(0,2,0),C1(0,2,2),E(2,2,1),F(0,0,1),B1(2,2,2),
建立如图所示的空间直角坐标系Dxyz.
典例讲解
所以=(0,2,1), =(2,0,0), =(0,2,1).
设=(x1,y1,z1)是平面的法向量,则⊥,⊥,由
令=2,则=-1,所以.
因为,所以.又C1平面,所以FC1∥平面ADE.
证明
例2、已知正方体ABCD -A1B1C1D1的棱长为2,E、F分别是BB1、DD1的中点,求证:FC1∥平面ADE.
典例讲解
变式演练
求证:平面ADE∥平面B1C1F.
由本例证明知=(2,0,0),设=(x2,y2,z2)是平面的一个法向量.
由⊥, ⊥ ,得从而
令得,所以
因为= ,
所以平面ADE∥平面B1C1F.
向量法证明线、面平行问题的方法
(1)用向量法证明线面平行:
①是证明直线的方向向量与平面内的某一向量是共线向量且直线不在平面内;
②是证明直线的方向向量可以用平面内两个不共线向量表示;
③是证明直线的方向向量与平面的法向量垂直且直线不在平面内.
(2)利用空间向量证明面面平行,通常是证明两平面的法向量平行.
方法归纳
2.在长方体ABCD -A1B1C1D1中,AB=4,AD=3,AA1=2,P,Q,R,S分别是AA1,D1C1, AB,CC1的中点.求证:PQ∥RS.
法一:以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系Dxyz.
变式训练
解析
则
从而(-3,2,1), (-3,2,1),即,故.
又P ,因此PQ∥RS.
法二:因为
所以.所以.又P ,因此PQ∥RS.
例3、如图,在直三棱柱ABC -A1B1C1中,AB⊥BC,AB=BC=2,BB1=2,E为BB1的中点.求证:平面AEC1⊥平面AA1C1C.
典例讲解
由题意得垂直,以为原点, 的方向分别为轴、轴、轴的正方向建立如图所示的空间直角坐标系,
解析
则从而=(-2,2,0),
设平面AA1C1C的法向量=(x1,y1,z1),则从而
令x1=1,得y1=1,所以=(1,1,0).
例3、如图,在直三棱柱ABC -A1B1C1中,AB⊥BC,AB=BC=2,BB1=2,E为BB1的中点.求证:平面AEC1⊥平面AA1C1C.
典例讲解
解析
因为·
所以⊥ ,所以平面AEC1⊥平面AA1C1C.
设平面AEC1的法向量
则从而
令=2,得,y2,所以
(1)用向量法判定线面垂直,只需直线的方向向量与平面的法向量平行或直线的方向向量与平面内两相交的直线的方向向量垂直即可.
(2)用向量法判定两个平面垂直,只需求出这两个平面的法向量,再看它们的数量积是否为0即可.
向量法证明线、面垂直问题的方法
方法归纳
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系(距离和夹角等);
(3)根据运算结果的几何意义来解释相关问题.
1.利用向量解决立体几何问题的“三步曲”
素养提炼
素养提炼
(1)选向量:在选取平面内的向量时,要选取不共线的两个向量.
(2)取特值:在求n的坐标时,可令x,y,z中一个为一特殊值得另两个值,就是平面的一个法向量.
(3)注意0:提前假定法向量n=(x,y,z)的某个坐标为某特定值时一定要注意这个坐标不为0.
2.求平面法向量的三个注意点
素养提炼
(1)在必修第二册中,我们学习了根据线面垂直、平行的判定定理和性质定理进行垂直和平行的判断,我们可称为综合法.
(2)利用空间向量的一组基底表示出向量,通过线性运算,根据向量共线的充要条件和数量积运算为0来达到判断平行和垂直的目的,此种方法我们称为向量基底法.
(3)建立空间直角坐标系,确定相关向量的坐标,利用空间向量的坐标运算达到判断平行和垂直的目的,此种方法我们称为向量坐标法.
3.立体几何证明方法总结
素养提炼
利用空间向量的坐标运算,可以把立体几何问题,先转化为向量问题,再转化为代数问题,从而建立几何和代数的联系,体现数形结合思想方法的应用.
对于一些以正方体、长方体或其他具备垂直关系的几何体作为载体的立体几何问题,可以优先考虑坐标法,这种方法的优点在于抛开了烦琐的推理论证,仅通过计算即可获得一些如平行、垂直等关系.
(1)数形结合的思想和类比思想,用空间向量表示立体几何中的点、线、面及其位置关系以及求线面角.
(2)没有运算,向量只能是路标
(3)直线的方向向量和平面的法向量尤为重要
归纳小结
(4)向量的加减、数乘和数量积运算的坐标表示;
(5)两个向量的夹角公式和垂直、平行判定的坐标表示.
(6)空间向量在立体几何中的简单运用.
P33 练习:1、2、3
作 业
人教A版同步教材名师课件
用空间向量研究直线、平面的位置关系
学习目标
学 习 目 标 核心素养
空间中点、直线和平面的向量表示 直观想象
数学抽象
空间中直线、平面的平行 直观想象
逻辑推理
空间中直线、平面的垂直 直观想象
逻辑推理
学习目标
学习目标:
1.了解空间中点、直线和平面的向量表示.
2.掌握直线的方向向量,平面的法向量的概念及求法.
3.熟练掌握用方向向量,法向量证明线线、线面、面面间的平行关系.
4.能利用平面法向量证明线面和面面垂直.
5.能利用直线的方向向量和平面的法向量判定并证明空间中的垂直关系.
学科核心素养:
1.通过空间中点、直线和平面的向量表示的学习,培养学生直观想象和逻辑推理的核心素养.
2.通过直线的方向向量和平面法向量的学习,培养学生数学运算的核心素养.
3.借助利用空间向量解决平行问题的学习,提升学生的数学运算及逻辑推理的核心素养.
4.借助空间向量证明线面垂直和面面垂直的学习,提升学生的数学运算和逻辑推理核心素养.
在空间中,取一定点作为基点,那么空间中任意一点的位置就可以用向量来表示.把向量称为点的位置向量.
P
·
o
·
问题1:怎样用向量表示点在空间中的位置?
东
南
A
45。
.C
北
实例:如图,如何叙述点的位置?如何找到(确定)空间的一个点
.
B
探究新知
问题2:在空间给定一个定点和一个定方向(向量),能确定一条直线在空间中的位置吗
我们把向量叫直线的方向向量,若仅研究两直线平行、垂直、成角时,可以用向量代替直线吗 直线的方向向量有多少个,为方便,我们一般怎样取出直线的方向向量
探究新知
O
A
l
P
探究新知
如图,为经过已知点A且平行于已知非零向量的直线,对空间任意一点O,点P在直线上的充要条件是
存在实数t,使,其中向量叫做直线的方向向量.
,
①和②都称为空间直线的向量表示式,空间任意直线由空间一点及直线的方向向量惟一决定.
由此可判断空间任意三点是否共线.
·
o
b
一个点和两个向量能确定一个平面
问题3:给一个定点和两个定方向,能确定一个平面在空间中的位置吗
探究新知
由平面向量基本定理知, 存在唯一的有序实数对,使得
空间一点位于平面内的充要条件是存在有序实数对使
C
探究新知
或对空间任一点O,有
C
③
③式称为空间平面的向量表示式,空间中任意平面由空间一点及两个不共线向量惟一确定.
O
探究新知
C
O
与共面
探究新知
探究新知
如图,直线.取直线的方向向量我们称向量为平面的法向量(normal vector).给定一个点和一个向量,那么过点且以向量为法向量的平面完全确定,可以表示为集合.
说说一个平面的法向量有多少个 平面的法向量与平面上的任意一个向量是什么关系
问题4:平面还有其它的向量表示吗
如果直线 ⊥平面,取直线的方向向量,则向量叫做平面的法向量.
探究新知
·
一个定点和平面的一个法向量,确定一个平面.若仅仅研究两平面平行、垂直、成角时,可以用平面的法向量代替吗
给定一个定点和一个平面的法向量,能确定一个平面在空间中的位置吗
探究新知
l
l⊥α u∥v u=λv
a1=λa2,b1=λb2,c1=λc2 (λ∈R).
l
探究新知
思考:设平面外的直线的方向向量是=(a1,b1,c1),平面的法向量是=(a2,b2,c2),若//,则向量和向量有什么关系?
若 ⊥,则向量和向量有什么关系?
l∥α ⊥ ·=0 a1a2+b1b2+c1c2=0.
设直线的方向向量分别为=(a1,b1,c1), =(a2,b2,c2),
l⊥m ·=0 a1b1+a2b2+a3b3=0
l∥m ∥ a=λ a1=λa2,b1=λb2,c1=λc2(λ∈R).
线线的关系
探究新知
设直线l的方向向量为=(a1,b1,c1),平面α的法向量为=(a2,b2,c2),则
l⊥α ∥ =λ a1=λa2,b1=λb2,c1=λc2(λ∈R).
线面的关系
l∥α ⊥ ·=0 a1a2+b1b2+c1c2=0.
探究新知
设平面的法向量分别为=(a1,b1,c1),=(a2,b2,c2),
⊥ ⊥ ·=0 a1a2+b1b2+c1c2=0.
面面的关系
∥ ∥ =λ a1=λa2,b1=λb2,c1=λc2(λ∈R).
探究新知
例1、已知A(1,0,1)、B(0,1,1)、C(1,1,0),求平面ABC的一个法向量.
典例讲解
设平面ABC的法向量为=(x,y,z),
由题意知=(-1,1,0), =(1,0,-1).
因为⊥且⊥,所以
令x=1,得y=z=1.
所以平面ABC的一个法向量为=(1,1,1).
解析
利用待定系数法求平面法向量的步骤
方法归纳
(1)设向量:设平面的法向量为=(x,y,z).
(2)选向量:在平面内选取两不共线向量.
(3)列方程组:由列出方程组.
(4)解方程组:
(5)赋非零值:取其中一个为非零值(常取±1).
(6)得结论:得到平面的一个法向量.
变式训练
1.如图所示,在四棱锥中,底面是直角梯形,,底面,且,建立适当的空间直角坐标系,分别求平面与平面的一个法向量.
如图,以为原点,以,分别为轴的正方向建立空间直角坐标系,则则
易知向量是平面的一个法向量.
解析
变式训练
1.如图所示,在四棱锥中,底面是直角梯形,,底面,且,建立适当的空间直角坐标系,分别求平面与平面的一个法向量.
解析
设=(x,y,z)为平面SDC的法向量,
则即
取x=2,则y=-1,z=1,
所以平面SDC的一个法向量为(2,-1,1).
例2、已知正方体ABCD -A1B1C1D1的棱长为2,E、F分别是BB1、DD1的中点,求证:FC1∥平面ADE.
则有D(0,0,0),A(2,0,0),C(0,2,0),C1(0,2,2),E(2,2,1),F(0,0,1),B1(2,2,2),
建立如图所示的空间直角坐标系Dxyz.
典例讲解
所以=(0,2,1), =(2,0,0), =(0,2,1).
设=(x1,y1,z1)是平面的法向量,则⊥,⊥,由
令=2,则=-1,所以.
因为,所以.又C1平面,所以FC1∥平面ADE.
证明
例2、已知正方体ABCD -A1B1C1D1的棱长为2,E、F分别是BB1、DD1的中点,求证:FC1∥平面ADE.
典例讲解
变式演练
求证:平面ADE∥平面B1C1F.
由本例证明知=(2,0,0),设=(x2,y2,z2)是平面的一个法向量.
由⊥, ⊥ ,得从而
令得,所以
因为= ,
所以平面ADE∥平面B1C1F.
向量法证明线、面平行问题的方法
(1)用向量法证明线面平行:
①是证明直线的方向向量与平面内的某一向量是共线向量且直线不在平面内;
②是证明直线的方向向量可以用平面内两个不共线向量表示;
③是证明直线的方向向量与平面的法向量垂直且直线不在平面内.
(2)利用空间向量证明面面平行,通常是证明两平面的法向量平行.
方法归纳
2.在长方体ABCD -A1B1C1D1中,AB=4,AD=3,AA1=2,P,Q,R,S分别是AA1,D1C1, AB,CC1的中点.求证:PQ∥RS.
法一:以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系Dxyz.
变式训练
解析
则
从而(-3,2,1), (-3,2,1),即,故.
又P ,因此PQ∥RS.
法二:因为
所以.所以.又P ,因此PQ∥RS.
例3、如图,在直三棱柱ABC -A1B1C1中,AB⊥BC,AB=BC=2,BB1=2,E为BB1的中点.求证:平面AEC1⊥平面AA1C1C.
典例讲解
由题意得垂直,以为原点, 的方向分别为轴、轴、轴的正方向建立如图所示的空间直角坐标系,
解析
则从而=(-2,2,0),
设平面AA1C1C的法向量=(x1,y1,z1),则从而
令x1=1,得y1=1,所以=(1,1,0).
例3、如图,在直三棱柱ABC -A1B1C1中,AB⊥BC,AB=BC=2,BB1=2,E为BB1的中点.求证:平面AEC1⊥平面AA1C1C.
典例讲解
解析
因为·
所以⊥ ,所以平面AEC1⊥平面AA1C1C.
设平面AEC1的法向量
则从而
令=2,得,y2,所以
(1)用向量法判定线面垂直,只需直线的方向向量与平面的法向量平行或直线的方向向量与平面内两相交的直线的方向向量垂直即可.
(2)用向量法判定两个平面垂直,只需求出这两个平面的法向量,再看它们的数量积是否为0即可.
向量法证明线、面垂直问题的方法
方法归纳
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系(距离和夹角等);
(3)根据运算结果的几何意义来解释相关问题.
1.利用向量解决立体几何问题的“三步曲”
素养提炼
素养提炼
(1)选向量:在选取平面内的向量时,要选取不共线的两个向量.
(2)取特值:在求n的坐标时,可令x,y,z中一个为一特殊值得另两个值,就是平面的一个法向量.
(3)注意0:提前假定法向量n=(x,y,z)的某个坐标为某特定值时一定要注意这个坐标不为0.
2.求平面法向量的三个注意点
素养提炼
(1)在必修第二册中,我们学习了根据线面垂直、平行的判定定理和性质定理进行垂直和平行的判断,我们可称为综合法.
(2)利用空间向量的一组基底表示出向量,通过线性运算,根据向量共线的充要条件和数量积运算为0来达到判断平行和垂直的目的,此种方法我们称为向量基底法.
(3)建立空间直角坐标系,确定相关向量的坐标,利用空间向量的坐标运算达到判断平行和垂直的目的,此种方法我们称为向量坐标法.
3.立体几何证明方法总结
素养提炼
利用空间向量的坐标运算,可以把立体几何问题,先转化为向量问题,再转化为代数问题,从而建立几何和代数的联系,体现数形结合思想方法的应用.
对于一些以正方体、长方体或其他具备垂直关系的几何体作为载体的立体几何问题,可以优先考虑坐标法,这种方法的优点在于抛开了烦琐的推理论证,仅通过计算即可获得一些如平行、垂直等关系.
(1)数形结合的思想和类比思想,用空间向量表示立体几何中的点、线、面及其位置关系以及求线面角.
(2)没有运算,向量只能是路标
(3)直线的方向向量和平面的法向量尤为重要
归纳小结
(4)向量的加减、数乘和数量积运算的坐标表示;
(5)两个向量的夹角公式和垂直、平行判定的坐标表示.
(6)空间向量在立体几何中的简单运用.
P33 练习:1、2、3
作 业
